Az arány szót hallván elsősorban nem, vagy nemcsak matematikai fogalomra gondolunk. Az arány, arányos szavak sokkal tágabban is értelmezhetők. De joggal mondhatjuk, az arányos szó alapvetően pozitív értelmezéssel bír.
Ha egy épület, egy test nem arányos, hanem aránytalan, azt nem szoktuk szépnek gondolni. Nem véletlen, hogy Arisztotelész az arányt a szépség elengedhetetlen kritériumának tartotta. Ha egy bírói ítéletről azt mondjuk, hogy aránytalanul enyhe vagy szigorú, azt is mondjuk, hogy nincs arányban az elkövetett vétséggel, azaz igazságtalan. A görögök ebben az értelemben az arányt etikai kategóriának tekintették, és tekinthetjük mi is.
Definíció:
A matematikában az arány két mennyiség, mérhető dolog viszonya. Maga a mérés is arány, hiszen méréskor a választott mértékegységhez viszonyítunk. Az arány két (azonos mértékegységben értett) érték hányadosával fejezhető ki.
Az arány matematikai fogalmát már az ókorban is ismerték. Eukleidész „Elemek” című könyvében össze is foglalta elődjei arányelméletét.
Az arány lehet racionális és irracionális is.
| Az arány racionális, ha két egész szám hányadosával, azaz racionális számmal fejezhető ki. Például a mellékelt ábrán a derékszögű háromszögek oldalainak egymáshoz viszonyított aránya racionális, hiszen BC=a=3 egység, CA=b=4 egység, így Pitagorasz tétele értelmében AB=c=5 egység. Ezért BC:AB=3:5, CA:AB=4:5, BC:CA=3:4. | 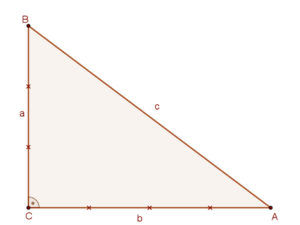 |
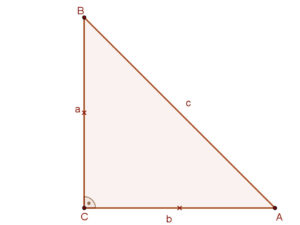 |
Már az ókori görögök is felismerték azonban, hogy az egyenlőszárú derékszögű háromszög átfogójának és befogójának aránya nem fejezhető ki racionális számmal. A mellékelt egyenlőszárú derékszögű háromszögben a háromszög átfogója a befogó \( \sqrt{2} \)-szerese. Azt is mondjuk, hogy az átfogó nem összemérhető a befogóval, mivel nincs olyan közös távolság, amelyik mindegyikre egész számszor felmérhető lenne. AB:BC=\( \sqrt{2} \) arányt irracionális aránynak is mondjuk. |
Szintén már az ókorban ismert volt, hogy a kör kerületének és az átmérőjének aránya állandó. Ezt az állandót nevezzük ma π-nek. Azt azonban akkor még nem tudták, hogy ez az arány szintén irracionális. Azonban míg a \sqrt{2} \)szerkeszthető, addig a π euklideszi módon nem szerkeszthető. Ez nyilvánul meg a kör négyszögesítése problémájában, amikor azt próbálták meg már az ókori görögök (Eratoszthenesz, Hippokratesz) is, hogyan lehetne egy adott körrel egyenlő területű, vagy kerületű négyzetet szerkeszteni.
Az arányok egyenlőségével aránypárhoz jutunk. A fenti első példán például BC:AB=3:5. Az aránypárt sokszor írjuk át szorzatalakba. Az egyenlőség két oldalán szereplő „belső” tényezők szorzata egyenlő a „külső” tényezők szorzatával. Ebben a példában: 3⋅AB=5⋅BC.
Arányos osztásról beszélünk, amikor, amikor egy adott mennyiséget adott arányban kell felosztani.
A mennyiségek közötti viszony, arány többféle is lehet. Az egyenes és fordított arányosságot bizonyára mindenki ismeri.
Egyenes arányosság fogalma:
Ha két változó mennyiség összetartozó értékeinek hányadosa, aránya állandó, akkor azt mondjuk, hogy az a két mennyiség egyenesen arányos.
Úgy is mondhatjuk, hogy ahányszorosára nő az egyik mennyiség, ugyanannyi szorosára nő a másik is.
Fordított arányosság fogalma:
Ha két változó mennyiség összetartozó értékeinek szorzata állandó, akkor azt mondjuk, hogy az a két mennyiség fordítottan arányos.
Úgy is mondhatjuk, hogy ahányszorosára nő az egyik mennyiség, ugyanannyiad részére csökken a másik.
A százalékszámítás szintén viszonyítás, amelyet az alábbi aránypárral fejezünk ki:
százalékérték: százalékalap=százalékláb:100.
A fenti összefüggés alapján bármelyik kettő ismeretéből a harmadik kiszámítható.
Az arány, arányosság alapvető matematikai fogalom, átszövi a középiskolai tananyagot is.
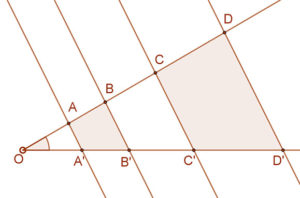
| Ha egy szög szárait párhuzamos egyenesekkel (e,f) metszük, akkor az egyik száron keletkezett szakaszok aránya egyenlő a másik száron keletkezett megfelelő szakaszok arányával. AB:CD=A’B’:C’D’. (Párhuzamos szelők tétele) |
 |
Középkorban Descartes a geometriai feladatoknál a szakaszok szorzásának és osztásának elvégzését az egységszakasz segítségével az un. negyedik arányos szerkesztésével valósította meg, amely a párhuzamos szelők tételén alapszik.
A hasonlóság fogalma is az arány fogalmához kapcsolódik. Két (akár sík, akár térbeli) alakzatot hasonlónak mondunk, ha a megfelelő pontjaikat összekötő szakaszok aránya megegyezik.
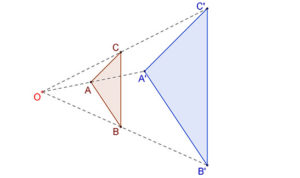
| Két (sík vagy térbeli) alakzat) középpontosan hasonló, ha pontjait összekötő egyenesek az adott O ponton (hasonlósági ponton) mennek át, és a pontoknak a hasonlóság középpontjától mért aránya állandó. ( λ hasonlóság aránya) OA’:OA=OB’:OB= OC’:OC=λ |
 |
Ha egy négyzet oldalát megháromszorozzuk, (egy adott pontból háromszorosára nagyítjuk), akkor a területe 32=9 szeresére nő. Általában is igaz, hogy hasonló síkidomok területének aránya a hasonlóság négyzetével, míg a hasonló testek térfogatának az aránya a hasonlóság arányszámának köbével egyenlő.
| Nézzük a mellékelt ábrát! Arkhimédész „A gömbről és hengerről” című munkájában meghatározta e testek felszínét és térfogatát. Azt, hogy a gömb felszíne egyenlő a köré írt henger palástjának területével. és a gömb térfogata a köré írt henger térfogatának 2/3-ad része, egyik legnagyobb felfedezésének tartotta. Ezért kérte. hogy halála után sírját egy hengerbe írt gömbbel jelöljék meg. | 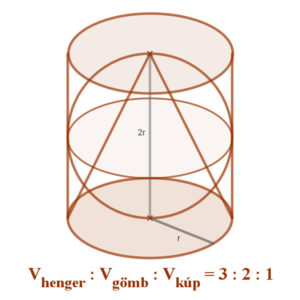 |
Arányosságok a háromszögben.
| A háromszögek súlyvonalai egy pontban, a súlypontban (S) metszik egymást. A súlypont a súlyvonalat harmadolja. Azaz: CS:SD=2:1 |
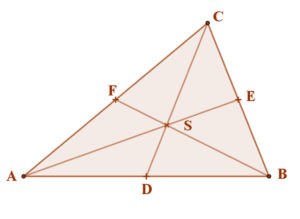 |
| Bármely háromszögben egy belső szög szögfelezője a szemközti oldalt a szomszédos oldalak arányában osztja két részre. A mellékelt ábra jelöléseit használva: CD:DB=AC:AB |
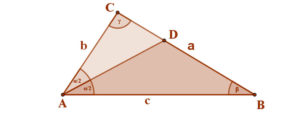 |
| A derékszögű háromszögben a befogó mértani közepe az átfogónak és az átfogóra eső merőleges vetületének. A mellékelt ábra jelöléseit használva: CB2=BA⋅BT, vagy a2=c⋅x, ill CA2=BA⋅AT, vagy b2=c⋅x A derékszögű háromszögben az átfogóhoz tartozó magasság mértani közepe az átfogó két szeletének. A mellékelt ábra jelölései szerint: CT2=BT⋅TA, vagy m2=y⋅x |
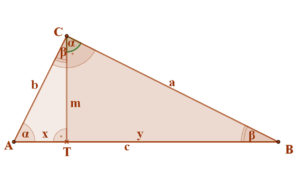 |
A derékszögű háromszögek oldalainak arányát hozzárendelve a hegyesszögekhez, megszületett trigonometria.
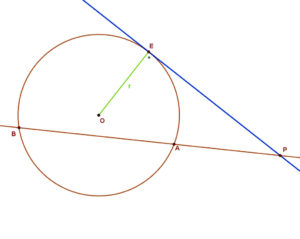 |
Ha egy (P) külső pontból egy körhöz egy szelőt és egy érintőt húzunk, akkor szelőnek a távolabbi metszéspontig (B) terjedő PA szakasza úgy aránylik az érintő (PE) szakasz hosszához, mint az érintőszakasz hossza aránylik a rövidebbik (PA) szelőszakaszhoz. Azaz: PB:PE=PE:PA. Szorzatalakba írva: PE2=PB⋅PA
|
Az aranymetszés:
Már régtől ismert, a természetben is megfigyelhető az az arány, amikor egy adott távolságot úgy osztunk fel két részre, hogy a kisebbik rész hossza úgy aránylik a nagyobbikhoz, mint a nagyobbik rész az egészhez.
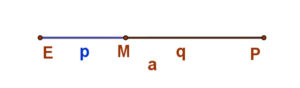 |
Azaz: EM:MP=MP:EP, vagy p:q=q:(p+q). Ezt az arányt aranymetszési aránynak nevezzük. |
 |
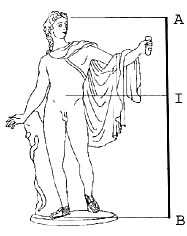 |
| „Divina proportio”, „isteni arány”, így nevezték az ókori matematikusok az aranymetszési arányt. Ezt az arányt annyira szépnek tartották, hogy nagyon sok műemlék arányaiban is felfedezhető. Így például a Belvederei Apollón szobron, amely Kr. e. 350. körül készült. Az „I” vel jelölt vonal az egész testet az aranymetszés arányának megfelelően osztja fel., azaz: AI:IB=IB:AB. | |
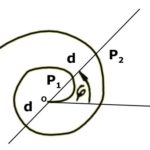 |
Az Arkhimédészi spirál esetén a spirál tetszőleges P pontjának a kezdőponttól való távolsága (r) egyenesen arányos az elfordulás szögével. Polárkoordinátás egyenlete: r=kj, ahol j az elfordulás szöge radiánban, és k egy állandó valós szám. |


1 hozzászólás
Comments are closed, but trackbacks and pingbacks are open.