Párhuzamos szelők tétele

Tétel:

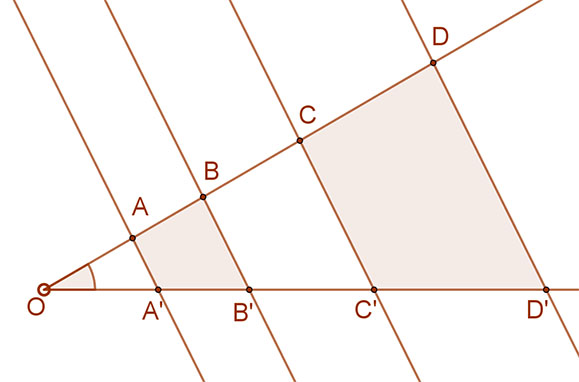Ha egy szög szárait párhuzamos egyenesekkel metsszük, akkor az egyik száron keletkező szakaszok hosszának aránya egyenlő a másik száron keletkező  megfelelő szakaszok hosszának arányával.

A mellékelt ábra szerint: AB:CD=A’B’:C’D’

A tétel feldolgozása három lépésből áll.

1. Elsőként belátjuk arra az esetre, amikor a párhuzamos egyenesek az egyik szögszáron egyenlő hosszúságú szakaszokat vágnak le, azaz az arányuk =1.
2. Ezután bizonyítjuk a tételt tetszőleges racionális arányra.
3. Irracionális arány esetén a középiskolában bizonyítás nélkül fogadjuk el a tételt .

1.  Nézzük tehát azt az esetet, amikor egy szög szárait párhuzamos egyenesekkel úgy vágjuk el, hogy az egyik száron keletkezett szakaszok egyenlők.

Azt kell belátnunk, hogy a másik száron is egyenlő hosszúságú szakaszok jöttek létre.

A mellékelt ábrán a feltétel szerint az „a” és „b” szögszárakat párhuzamos egyenesekkel metszettük, és feltételezzük, hogy AB=CD, azaz AB:CD=1.
Azt kell belátnunk, hogy akkor A’B’=C’D’ is igaz, tehát ebben az esetben AB:CD=A’B’:C’D’=1

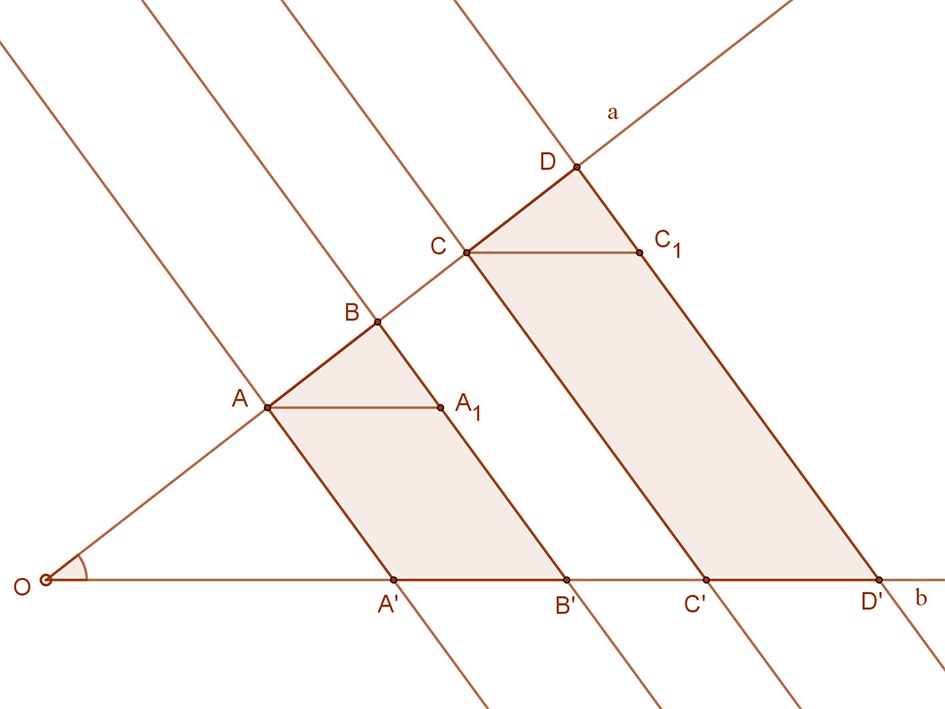Húzzunk az A illetve C pontokból párhuzamosokat a b szögszárral. Így kapjuk az A₁ és C₁ pontokat.
Az így kapott háromszögek egybevágóak, azaz AA₁B≅CC₁D, hiszen megfelelő szögeik egyállásúak (párhuzamosságok miatt), és van egy egyenlő oldaluk, hiszen a feltétel szerint AB=CD. A háromszögek egybevágóságából következik, hogy AA₁=CC₁
Az A’B’A₁A és C’D’C₁C négyszögek paralelogrammák. Ezért AA₁=A’B’ és CC₁=C’D’.
Mivel azonban AA₁=CC₁, ezért A’B’=C’D’. És ezt akartuk belátni.

2. Ezután bizonyítjuk a tételt tetszőleges racionális arányra.

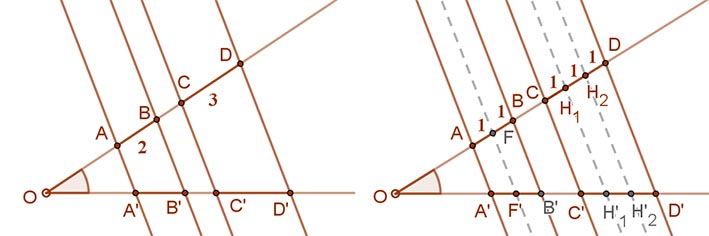Az adott racionális (p:q) arány esetén ( a mellékelt oldali képen ez 2:3) felosztjuk az AB illetve a CD szakaszokat p és q részre, azaz egységnyi és egyenlő hosszúságú szakaszokra. Az osztópontokon át párhuzamosokat húzva visszavezettük ezt az esetet az előző, már bizonyított esetre.

Vajon igaz-e a tétel megfordítása?

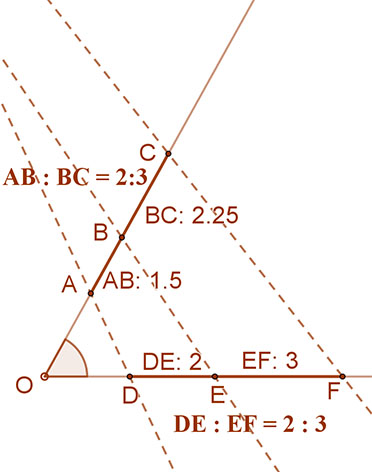
A mellékelt ábrán a szög szárait metsző egyenesek a szárakon egyenlő arányú szakaszokat hoznak létre, az egyenesek mégsem párhuzamosak!
Figyelembe kell venni a szög szárain keletkezett többi szakaszt, így a szög csúcsánál kezdődő szakaszokat is.

A tétel megfordítása helyesen:

Ha két egyenes egy szög száraiból olyan szakaszokat vág le, amelyeknek hosszának aránya mindkét száron egyenlő, akkor a két egyenes párhuzamos.

Ezek után felmerül a kérdés, milyen összefüggés írható fel a párhuzamos egyeneseknek a szög szárai közé eső szakasza és a szög szárain keletkezett szakaszok között?

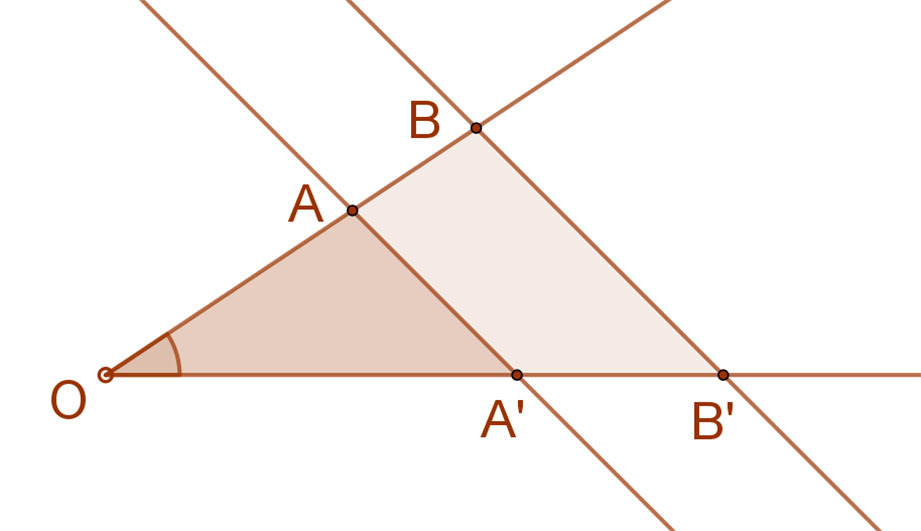Igaz-e a mellékelt ábrán, hogy AA’:BB’= OA:AB?

Ez így nem igaz, sok hiba forrása.
A BB’ szakaszhoz megfelelő szakasz nem az AB, hanem az OB!
A mellékelt ábrán az OAA’ háromszög hasonló az OBB’ háromszöghöz, hiszen oldalai párhuzamosak, így szögei egyenlők.
Ezért oldalainak aránya egyenlő, azaz AA’:BB’=OA:OB vagy AA’:BB’=OA’:OB’.

Tétel szavakkal:

Egy szög szárait metsző párhuzamosokból a szárak által kimetszett szakaszok aránya megegyezik a párhuzamosok által az egyik szögszárból kimetszett szakaszok arányával.
Ezt az összefüggést szokás párhuzamos szelőszakaszok tételének is nevezni.

Alkalmazás:

Párhuzamos szelők tételét alkalmazzuk adott szakasz adott arányban történő felosztására.

Descartes nyomán a párhuzamos szelők tételével, valamint egység szakasz ismertében tudunk szakaszok szorzatát, hányadosát, négyzetét és reciprokát szerkeszteni. (Negyedik arányos szerkesztése.)

Feladat

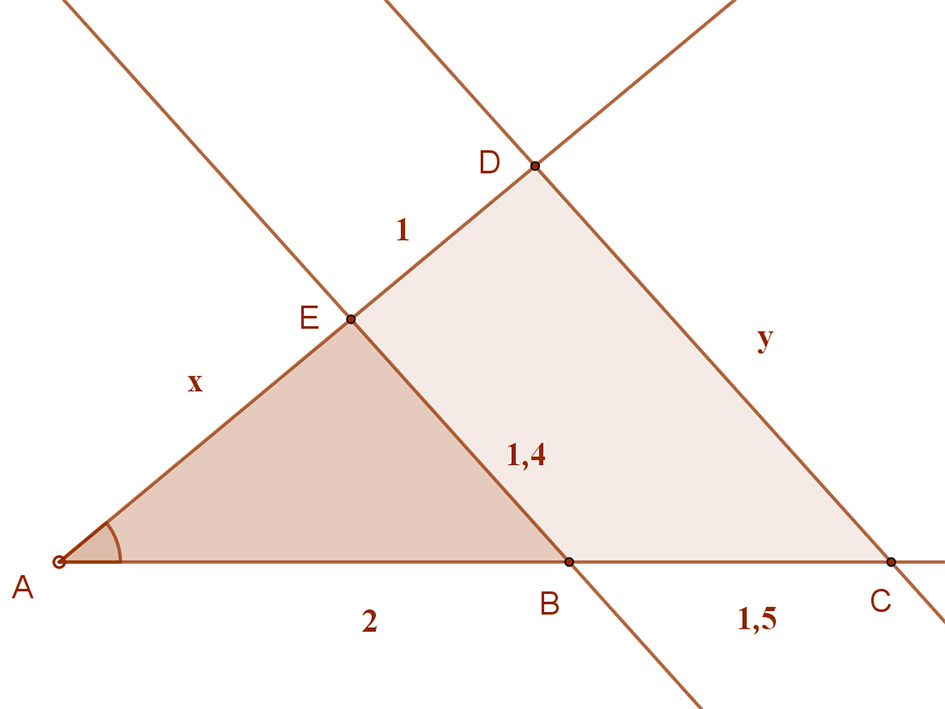
A mellékelt ábrán BE||CD. Mekkora x és y?

Megoldás:

Párhuzamos szelők tétele szerint: AB:BC=AE:ED. Azaz 2:1,5=x:1
Tehát x=2:(3/2), azaz x=4/3.
Másrészt  a párhuzamos szelőszakaszok tételének megfelelően
AB:AC=BE:y, azaz 2:3,5=1,4:y. Így y=3,5⋅1,4/2, tehát y=4,9/2, y=2,45.