Definíció:
Azok a számok, amelyek nem racionálisak, azaz amelyek nem írhatók fel két egész szám hányadosaként irracionális számoknak nevezzük.
Jele: ℚ*
Végtelen nem szakaszos tizedes törtek. Ilyet mi is készíthetünk.
Például: 2,303003000300003000003….
Látszik az eljárás, mindig eggyel több nullát írunk a hármasok közé. Az így kapott szám biztosan végtelen és nem szakaszos tizedes tört.
Kimutatható, hogy az irracionális számok „sokkal többen” vannak, mint a racionálisak. Ez először meglepőnek tűnik. Hiszen ha megkérdezünk valakit, soroljon fel irracionális számokat, akkor a \( \sqrt{2} \) és a π jutna az eszébe.
Ha azonban azt is mérlegeljük, hogy egy racionális szám és egy irracionális szám összege (különbsége) irracionális szám, illetve ha egy nem 0 racionális szám és egy irracionális szám szorzata (hányadosa) irracionális szám, akkor már érthetőbb a dolog.
Az irracionális számok halmazának számossága meghaladja a racionális számok halmazának számosságát és megegyezik a valós számok számosságával, azaz kontinuumnyi számosságú.
Ha viszont két irracionális számot összeadunk (kivonunk) vagy összeszorzunk (elosztunk) egymással, nem biztos, hogy irracionális számot kapunk.
Nyilvánvaló példák: \( \sqrt{2}-\sqrt{2}=0 \), vagy \( \sqrt{2}⋅\sqrt{2}=2 \)
Az irracionális számok aritmetikai elméletének kidolgozása elsősorban Cantor munkásságának eredménye.
Az irracionális számok két csoportba sorolhatók.
- Vannak olyan irracionális számok, amelyek gyökei racionális együtthatójú algebrai egyenletnek. Ilyen például a \( \sqrt{2} \), Hiszen az x2-2=0 egyenlet egyik gyöke .
- Vannakaz un. transzcendens számok. Ezek olyan irracionális számok, amelyek nem gyökei semmilyen racionális együtthatójú algebrai egyenletnek. Legnevezetesebb közülük a π, a Ludolph féle szám.
Megjegyzés: Egy számot algebrai számnak mondunk, ha van olyan racionális együtthatójú algebrai egyenlet, amelynek ő gyöke.
A racionális számok mindegyike, és az irracionális számok egy része algebrai szám.
Az irracionális számok egy része euklideszi módon szerkeszthető. Például a \( \sqrt{2} \). Más részük azonban így nem szerkeszthető. Ilyen például a \( \sqrt[3]{2} \), vagy a π, a Ludolph féle szám.
Az irracionális és racionális számokat együtt valós számoknak nevezzük.
Jele: ℝ.
A valós számok és a számegyenes pontjai között kölcsönösen egyértelmű megfeleltetés részesíthető.
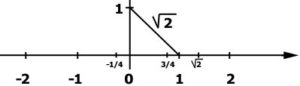
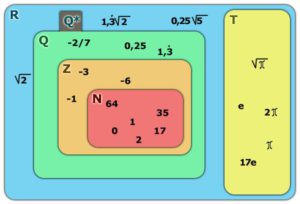 A különböző számhalmazokat, a számfogalom bővülésének megfelelően a mellékelt ábrán egy Venn-diagrammal lehet szemléltetni.
A különböző számhalmazokat, a számfogalom bővülésének megfelelően a mellékelt ábrán egy Venn-diagrammal lehet szemléltetni.
Az egyes számhalmazok és betűjele:
ℕ: Természetes számok halmaza
ℤ: Egész számok halmaza.
ℚ: Racionális számok halmaza.
ℚ*: Irracionális számok halmaza.
\( \mathbb{T} \): Transzcendens számok halmaza
ℝ: Valós számok halmaza
Az irracionális számokat már igen régen ismerték a matematikusok. Mezopotámiában a kb. i.e. 600-300-ban keletkezett egyik táblázat szerint: \( \sqrt{2}≈1\frac{25}{60} \)
Ez a közelítő érték a mai írásmódunk szerint tizedes tört alakban 1,4167. Az irracionális viszonyt, illetőleg az irracionális számot Pitagorasz tanítványai a püthagoreusok fedezték fel az i.e. V. században, minden valószínűség szerint a négyzet átlójával kapcsolatban. A másik igen korai ismert irracionális szám a p , mint az egységsugarú kör félkerülete lehetett, de erről csak a XVIII. században tudták bebizonyítani, hogy irracionális. Először a \( \sqrt{2} \)-ről (az egységnyi hosszúságú négyzet átlójáról.) bizonyították be (Eukleidész), hogy irracionális.


Comments are closed, but trackbacks and pingbacks are open.