Arányos osztás

Gyakori feladat, amikor egy adott mennyiséget egy megadott aránynak megfelelően kell felosztani.

Hogyan osztunk fel 36000 Ft-ot két ember között 5:7 arányban?

Ha a felosztandó összeget 5+7=12 egyenlő részre felosztjuk, akkor az egyik ember ennek az egységnek ötszörösét, a másik a 7-szeresét kapja. Azaz: 36000:12=3000 Ft.

Így az egyik ember 5⋅3000=15000 Ft-t, a másik ember 7⋅3000=21000 Ft-t fog kapni.

Természetesen ez a feladat is felírható aránypárral.
Ha x jelöli az egyik embernek járó összeget, akkor nyilván a másiknak 36000-x Ft jár. Így az aránypár: x:(36000-x)=5:7.
Szorzatalakba írva: 5⋅(36000-x)=7x. Azaz 5⋅36000-5x=7x.
Így: 5⋅36 000=12x. Az x kifejezve: x=5⋅36000/12.
Tehát x= 15000 Ft.

Az első -1527-ből fennmaradt magyar matematika tankönyvben, a „Debreceni Aritmetiká”-ban is szerepel ilyen jellegű feladat.

Geometriában egy adott szakasz arányos osztását párhuzamos szelők tétele segítségével végezzük el.

Legyen adott egy tetszőleges hosszúságú AB szakasz. Osszuk ezt fel 2:3 arányban úgy, hogy a keresett „C” pont az „A” ponthoz legyen közelebb. Azaz AC:CB=2:3 legyen.

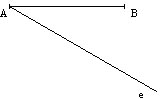Húzzunk a szakasz egyik (mondjuk „A”) végpontjából a szakasszal tetszőleges szöget (praktikusan hegyesszöget) bezáró „e” segédegyenest.

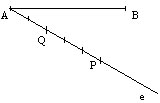Mérjünk erre rá egy tetszőleges hosszúságú szakaszt 2+3=5-ször. A második mérésnél kapott pontot nevezzük el „Q”-nak, a végpontot meg „P”-nek. Itt AQ:QP=2:3.

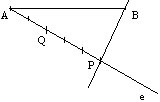Az így kapott „P” pontot kössük össze a szakasz másik (azaz „B”) végpontjával.

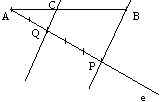A „e” segédegyenes „Q” pontjából húzzunk párhuzamost a PB egyenessel. Ez kimetszi az AB szakaszon a keresett „C” pontot, hiszen a párhuzamos szelők tétele szerint: AQ:QP=AC:CB=2:3.

Koordináta-geometriában ugyanezen elv alapján történik egy adott szakasz felezési és harmadoló pontjának koordinátáinak meghatározása.