Analitikus geometria

Az analitikus (koordináta) geometriában a geometriai feladatokat algebrai eszközökkel oldunk meg. Ehhez szükség van egy koordináta rendszerre, amelynek segítségével a pontokhoz koordinátákat rendelhetünk.

Az alakzatokat egy, a pontjaira vonatkozó összefüggéssel, az alakzat egyenletével adunk meg. A koordináta-rendszert bázisvektorok segítségével definiáljuk. A függvények grafikonjait is koordináta rendszerben ábrázoljuk.

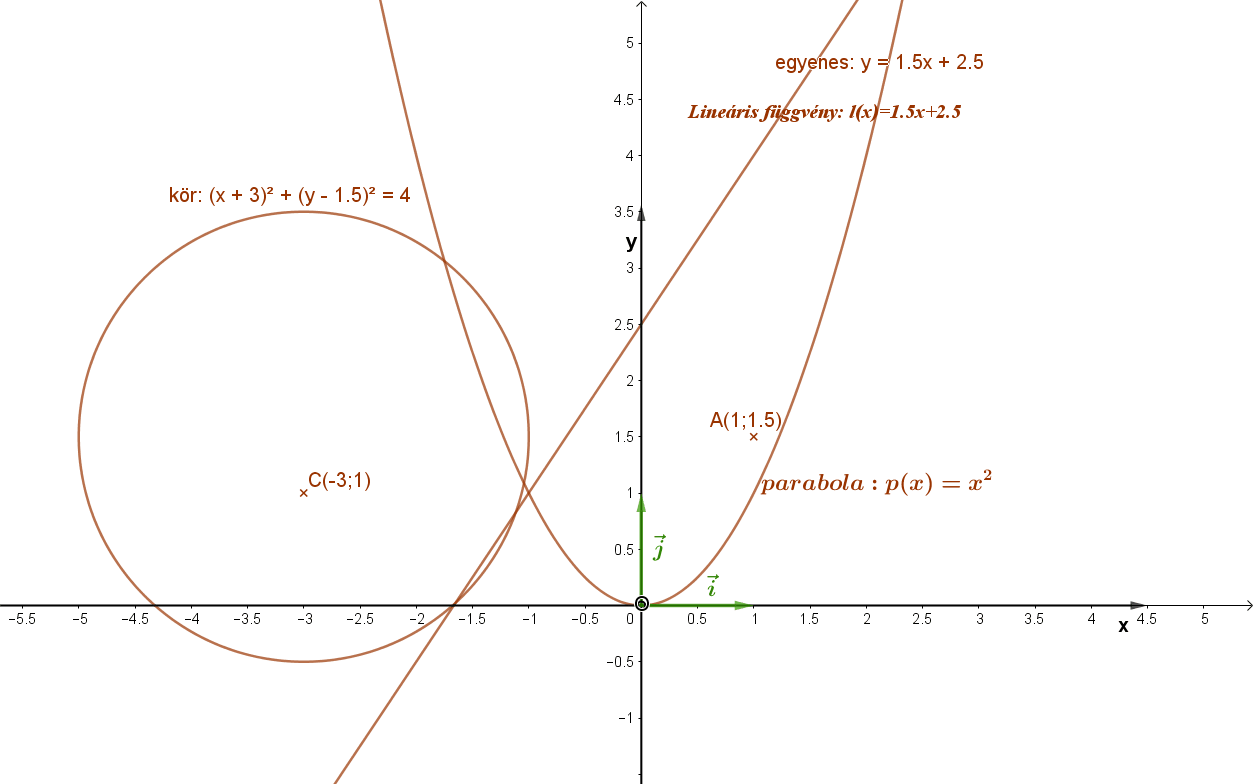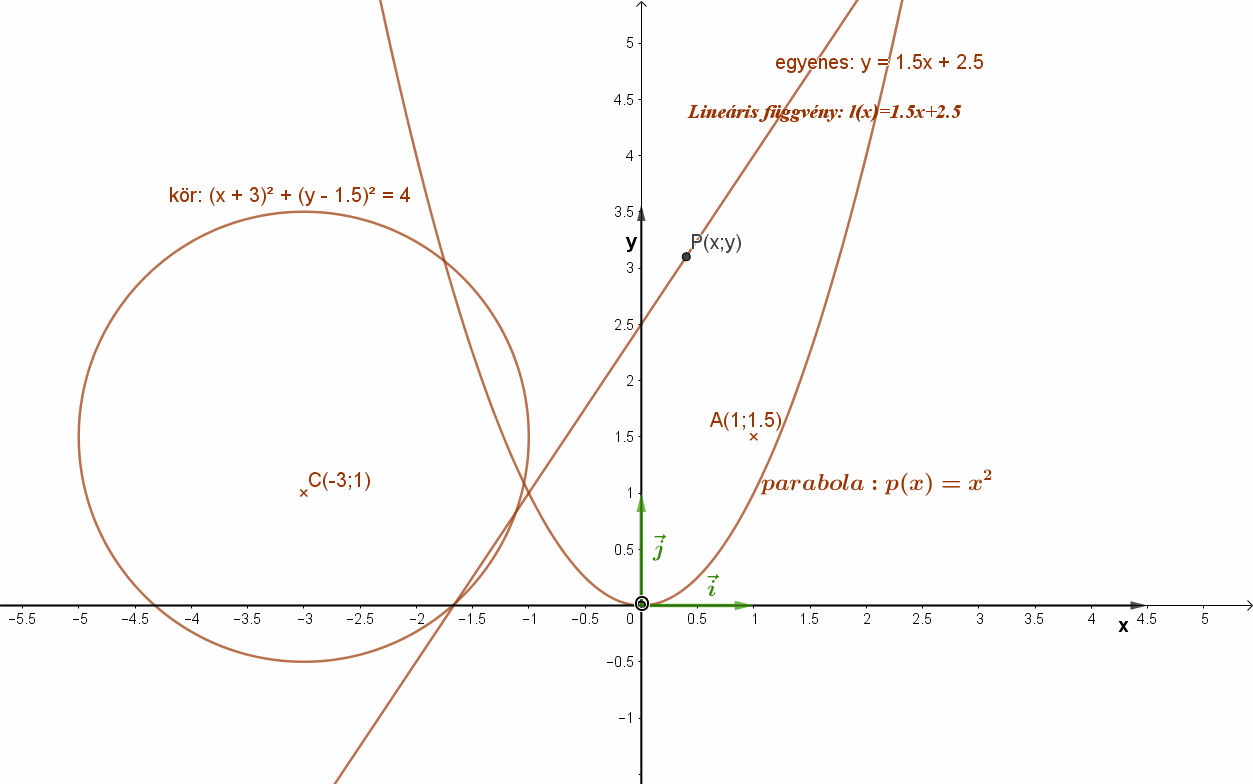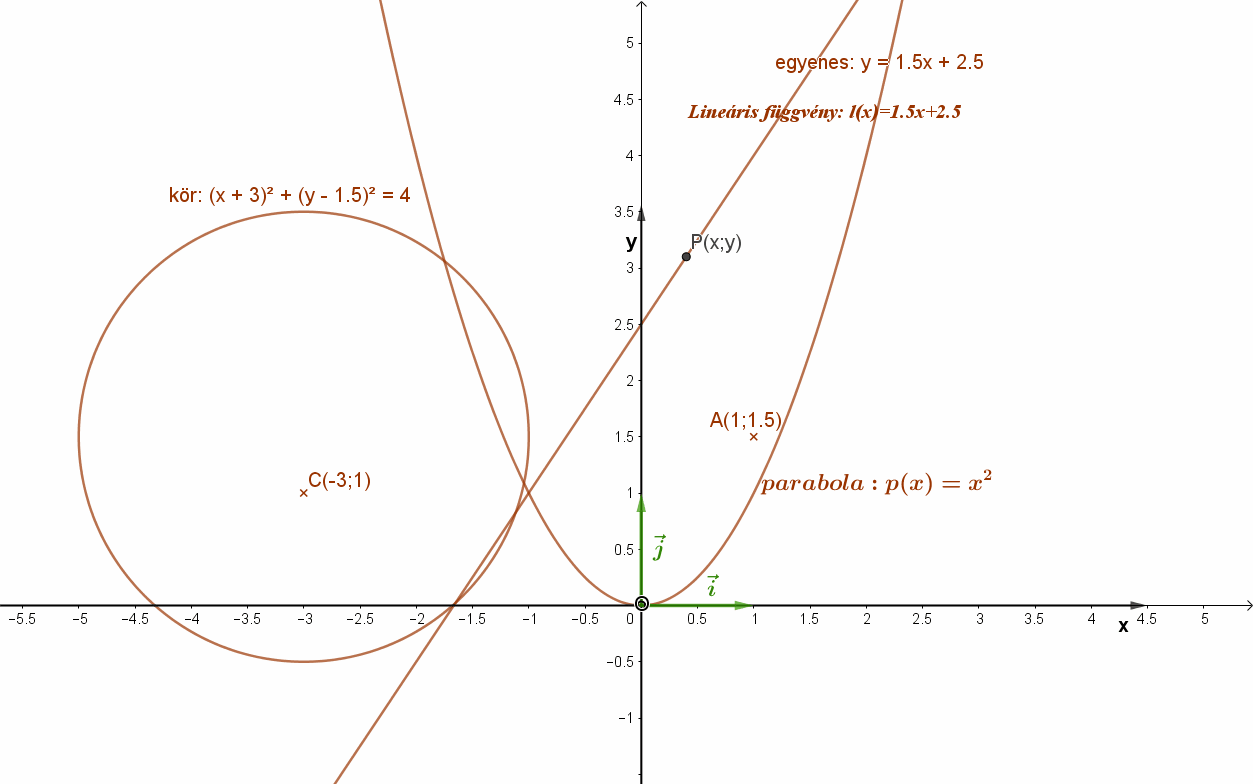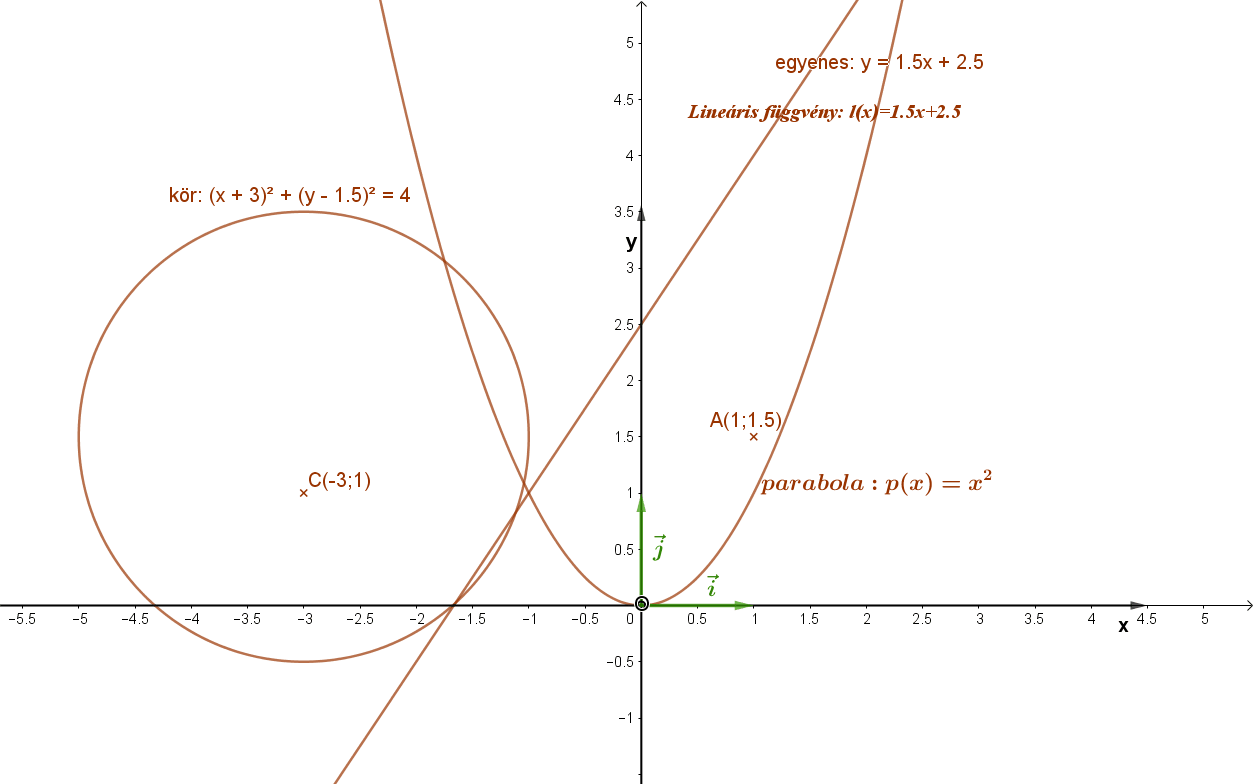
A fenti animációban láthatunk pontokat: (A, C, P), alakzatokat (egyenes kör, parabola) és függvényeket is. (lineáris függvény (egyenes), másodfokú függvény (parabola)).

Persze, ennek a matematikai szakterületnek is megvannak a maga történelmi előzményei.

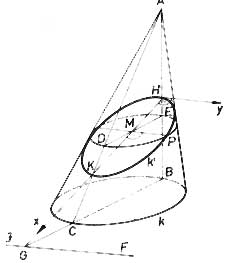
Apollóniosz fő művében, a 8 kötetes „Kónika-ban”, a kúpszeletek (ellipszis, parabola, hiperbola) tárgyalásánál a kúpszeleteket egy ferde kettős körkúp síkmetszeteiként tárgyalta. Mivel mindent a kúpszeletek átmérőire vonatkoztatott, ez már a koordináta-geometria tárgyalás irányába mutat. Ő azonban nehézkesen, egyetlen tengellyel és negatív számok nélkül dolgozott.

Ptolemaiosz „Geographia” művében a Föld egy pontjának helyét lényegében a mai földrajzi szélességnek és hosszúságnak megfelelő adatokkal határozta meg, tehát gömbi koordinátákat használt.

Descartes a geometria problémák megoldásához gyakran alkalmazott algebrai módszereket. Az 1637-ben megjelent Értekezések a módszerről című könyvének függeléke a Geometrie, amely lendületet adott az analitikus geometria fejlődésének. Műveiben azonban még nem szerepel a koordináta rendszer, amely pedig ma az ő nevét viseli. Descartes Apollóniosz-hoz hasonlóan még csak egyetlen tengellyel dolgozott, és ezen sem vette figyelembe a negatív számokat, bár már számolt is velük, „hamis” számoknak nevezte őket.

Fermat francia matematikus 1679-ben „Isagoge” című tanulmánya már analitikus geometriai tárgyúnak mondható.

Leibniz használta először többek között a koordináta elnevezéseket.

Isaac Newton angol matematikus és fizikust követően, Euler 1748-ban megjelent könyvében már olyan koordináta rendszerrel találkozunk, amelynek két tengelye volt, és már negatív számokkal is dolgozott. Ebben a könyvében Euler egyes görbék és felületek tulajdonságait vizsgálta, egyenleteik alapján.