A másodfokú függvény és jellemzése

Definíció:

Az f:ℝ→ℝ,f(x) másodfokú függvény általános alakja: f(x)=ax²+bx+c, ahol a, b és c valós értékű paraméterek. (a∈ℝ és a≠0, b∈ℝ, c∈ℝ)

A másodfokú függvény grafikonja egy olyan parabola, amelynek a szimmetriatengelye párhuzamos az y tengellyel. Ennek a parabolának általános egyenlete tehát: y=ax² +bx+c.

A legegyszerűbb másodfokú függvény paraméterei: a=1, b=0, c=0.
Ekkor a függvény képlete: f(x)=x².

Ennek grafikonja: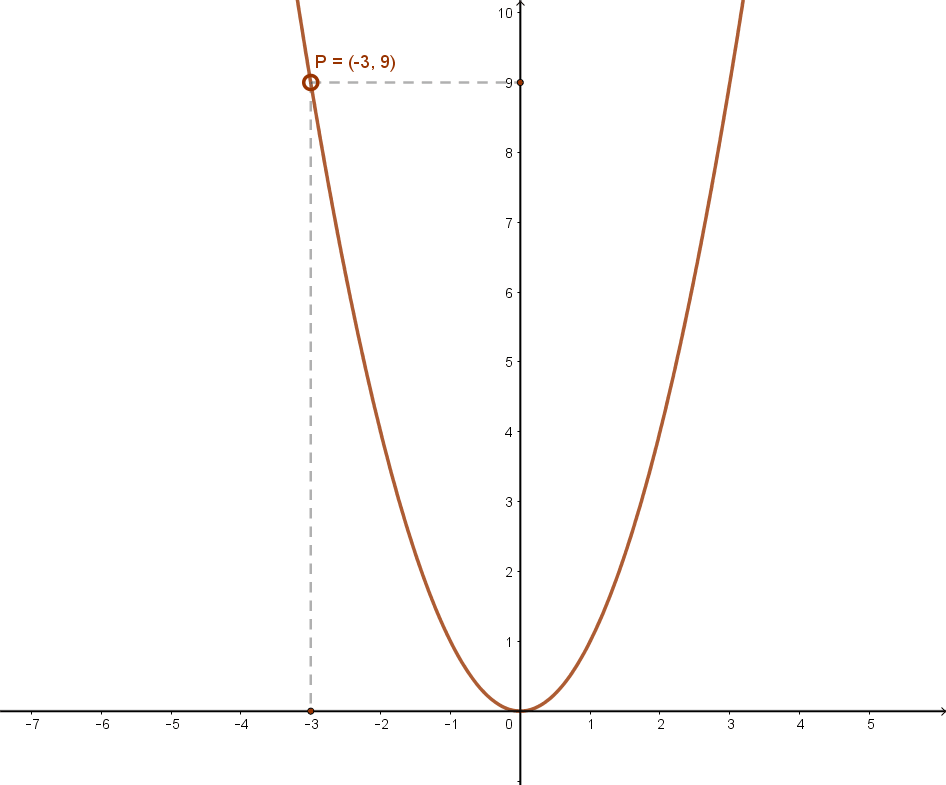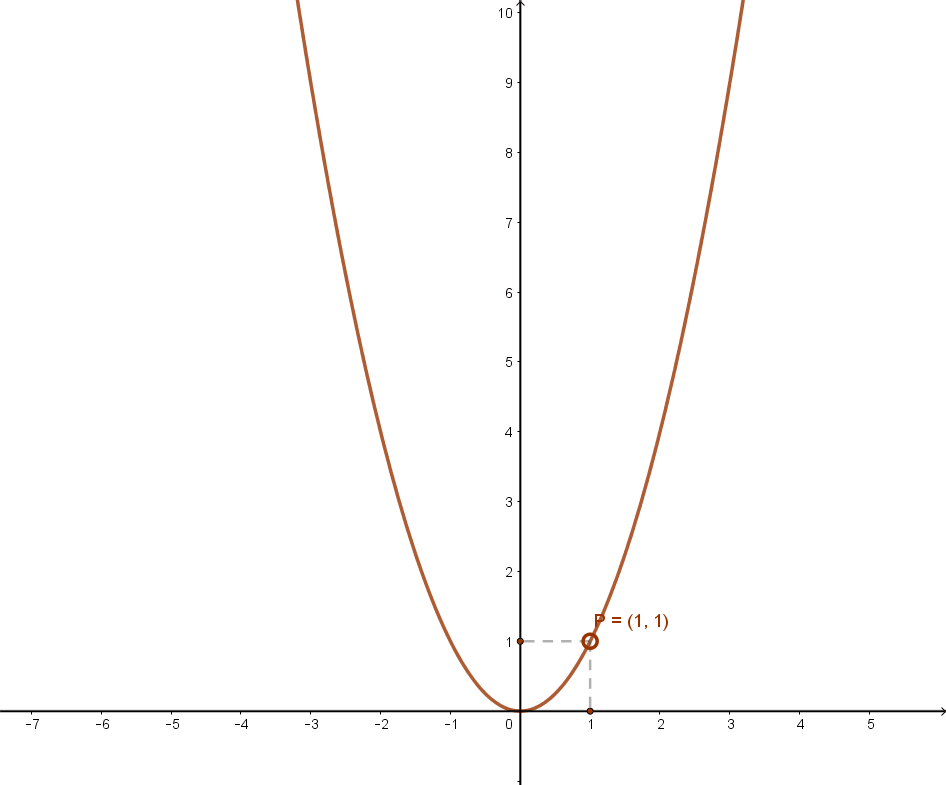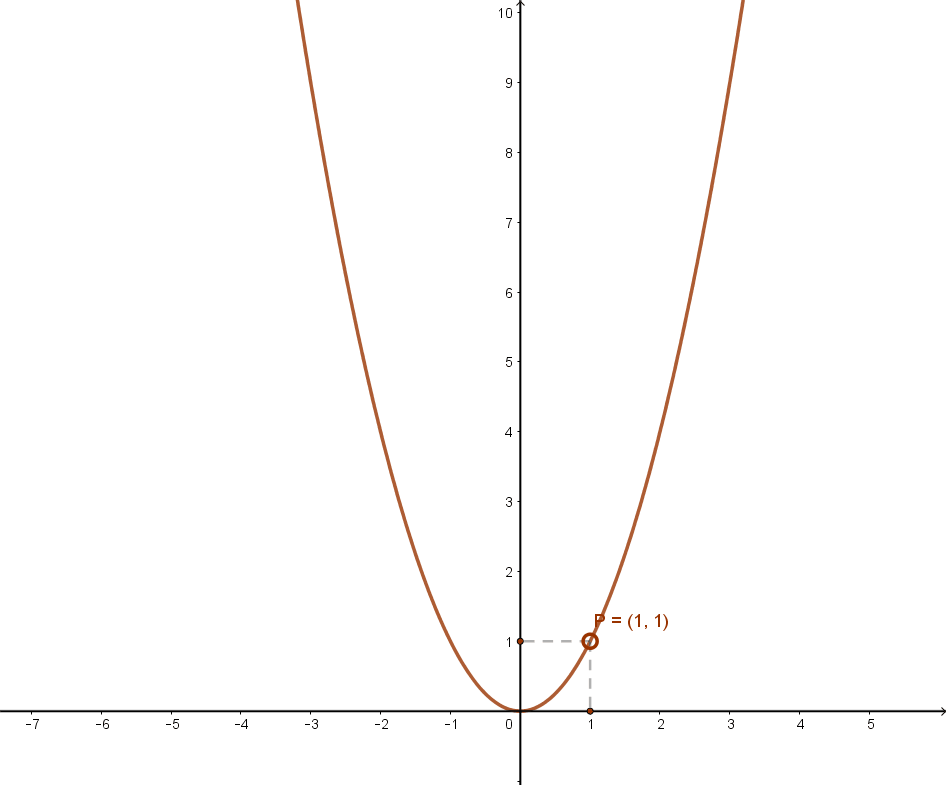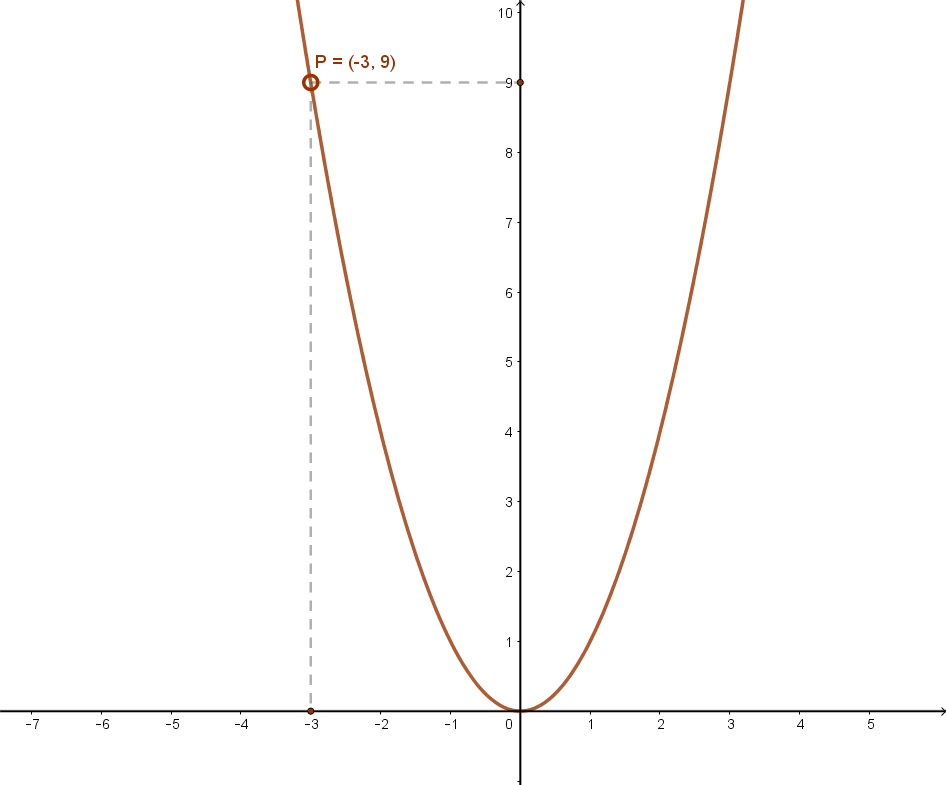

Az f(x)=x² függvény jellemzése:

Értelmezési tartomány:	x∈ℝ.
Értékkészlet:	y=x2∈R|y≥0.
Zérushelye:	Az x2=0 egyenlet megoldása: x=0.
Menete, monotonitása:	Szigorúan monoton csökken, ha x<0 és szigorúan monoton nő, ha x>0.
Szélsőértéke:	Minimum, x=0, y=0.
Korlátos:	Általános értelemben nem, alulról igen: k=0.
Páros vagy páratlan:	Páros.
Periodikus:	Nem.
Konvex/konkáv:	Konvex.
Folytonos:	Igen.
Inverz függvénye:	Van, ha x≥0. Ez a ​\( \sqrt{x} \)​ négyzetgyök függvény.

Legyenek most a másodfokú függvény paraméterei például: a=1, b=6, c=5.
Ekkor függvény képlete: f(x)=x²+6x+5.
Ez teljes négyzetté alakítás után a következő transzformációs alakra hozható: f(x)=(x+3)²-4.
Az  f(x)=x² függvény el van tolva az „x” tengely mentén balra 3 egységgel és le van tolva az „y” tengely mentén 4 egységgel.

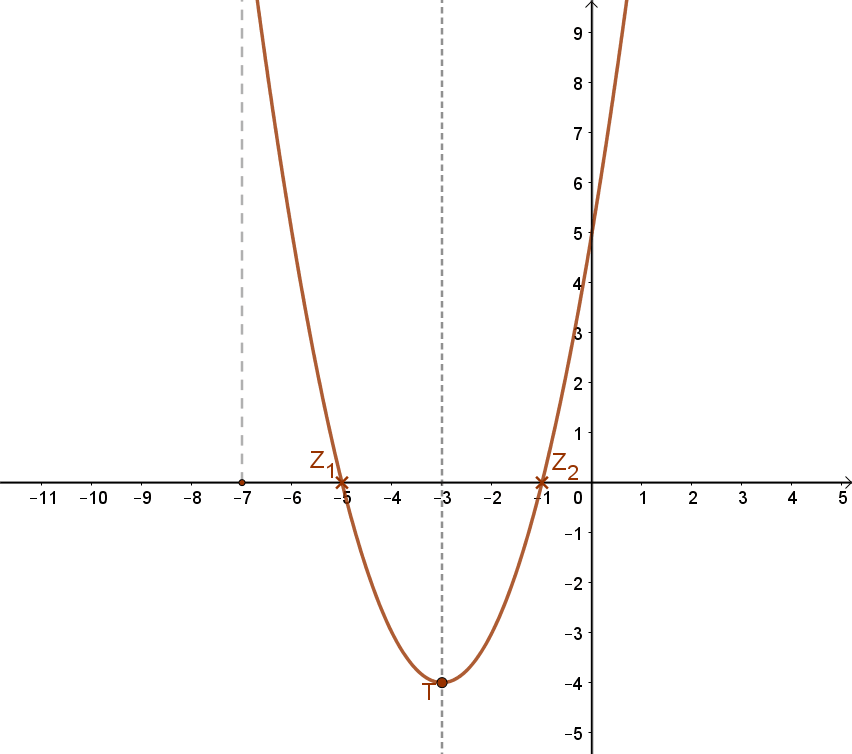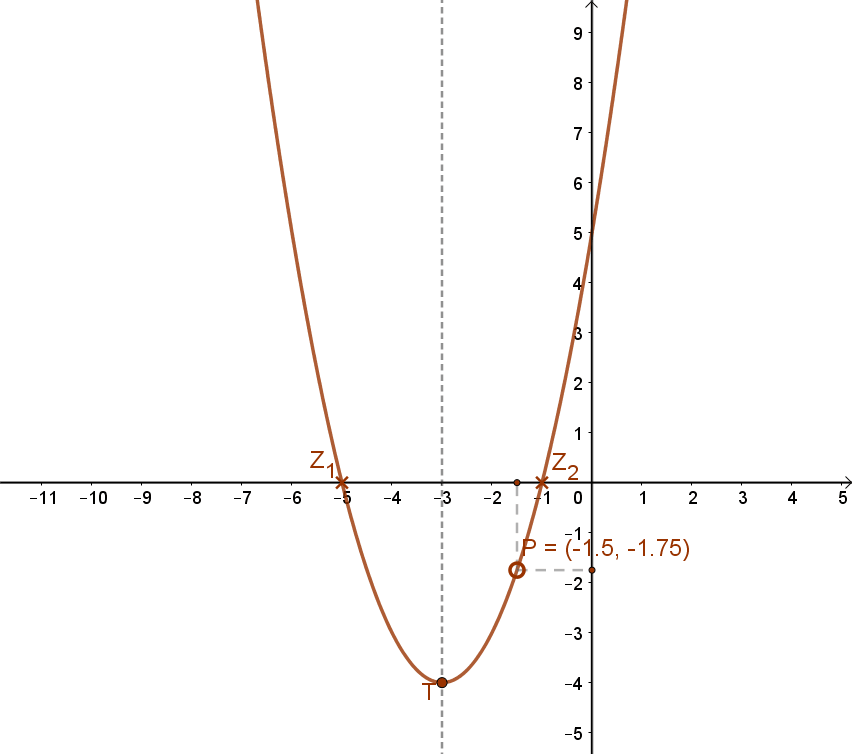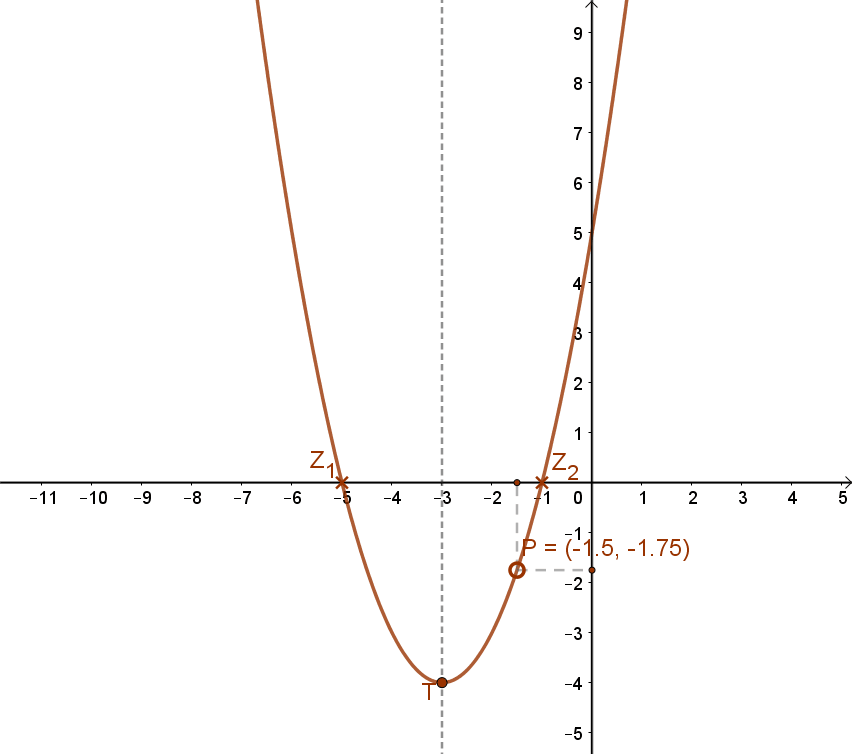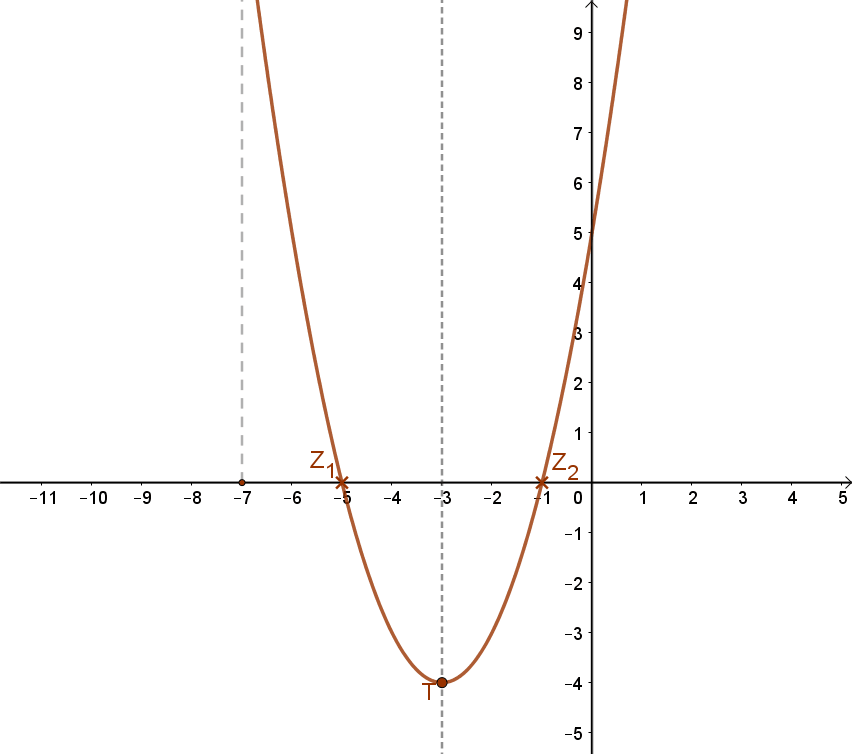
Az  f(x)=(x+3)²-4 függvény grafikonja:

Az f(x)=x²+6x+5 =(x+3)²-4 függvény jellemzése:

Értelmezési tartomány:	x∈ℝ.
Értékkészlet:	y=x2∈R|y≥-4.
Zérushelye:	Az x2+6x+5=0 másodfokú egyenlet megoldása után: Z1(-5;0) és Z2(-1;0)
Menete, monotonitása:	Szigorúan monoton csökken, ha x<-3 és szigorúan monoton nő, ha x>-3.
Szélsőértéke:	Minimum, T(-3;-4)
Korlátos:	Általános értelemben nem, alulról igen: k=-4.
Páros vagy páratlan:	Egyik sem.
Periodikus:	Nem.
Konvex/konkáv:	Konvex.
Folytonos:	Igen.
Inverz függvénye:	Van, ha x≥-4. Ez a ​\( \sqrt{x+4}-3 \)​ négyzetgyök függvény.

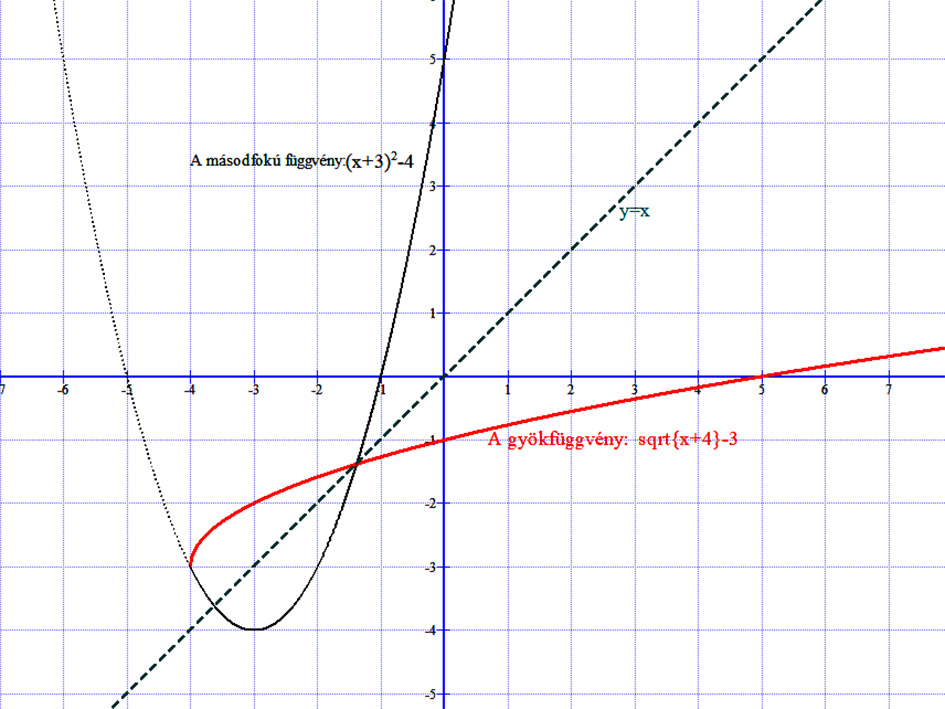
Az f(x)= x²+6x+5 =(x+3)²-4 másodfokú függvény és inverzének, a ​\( g(x)=\sqrt{x+4}-3 \)​ négyzetgyök függvénynek a grafikonja.