Definíció:
Az f: R→R, f(x) elsőfokú függvény általános alakja: f(x)=ax+b, ahol a és b valós értékű paraméterek. (a∈ℝ és a≠0, b∈ℝ.)
Az elsőfokú függvény grafikonja egy olyan egyenes, amely nem párhuzamos sem az x sem az y tengellyel.
Az a paramétert az egyenes meredekségének nevezzük, a b paraméter pedig megmutatja, hogy hol metszi az egyenes az y tengelyt: a (0;b) koordinátájú pontban.
Az elsőfokú függvényt grafikonja után lineáris függvénynek is szokták nevezni. (Linea=vonal, egyenes).
Viszont nem minden lineáris függvény elsőfokú. Az f(x)=c nullad fokú függvény is lineáris függvény, grafikonja olyan egyenes, amely párhuzamos az x tengellyel.
Az elsőfokú függvény grafikonjának általános egyenlete tehát: y=ax +b.
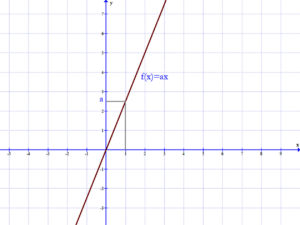
Ha az elsőfokú függvénynél b=0, akkor a függvény szabálya: f(x)=ax.
Ekkor az egyenes arányosság függvényét kapjuk. Ennek grafikonja egy, az origón átmenő egyenes.
A következő elsőfokú függvény paraméterei: a=-0.5 (meredekség), b=+3
Ennek megfelelően a függvény szabálya: f(x)=-0.5x+3.
Így a függvény grafikonja:
Az f(x)=-0.5x+3 elsőfokú függvény jellemzése:
| Értelmezési tartomány: | x∈ℝ. |
| Értékkészlet: | y=-0.5x+3∈ℝ. |
| Zérushelye: | A -0.5x+3=0 elsőfokú egyenlet megoldása: Z(6;0). |
| Menete: | Szigorúan monoton csökken a teljes értelmezési tartományon. |
| Szélsőértéke: | Nincs. |
| Korlátos: | Nem. |
| Páros vagy páratlan: | Egyik sem. |
| Periodikus: | Nem. |
| Konvex/konkáv: | Egyik sem. |
| Folytonos: | Igen. |
| Inverz függvénye: | Van. Szintén lineáris függvény. f(x)=-2x+6. |
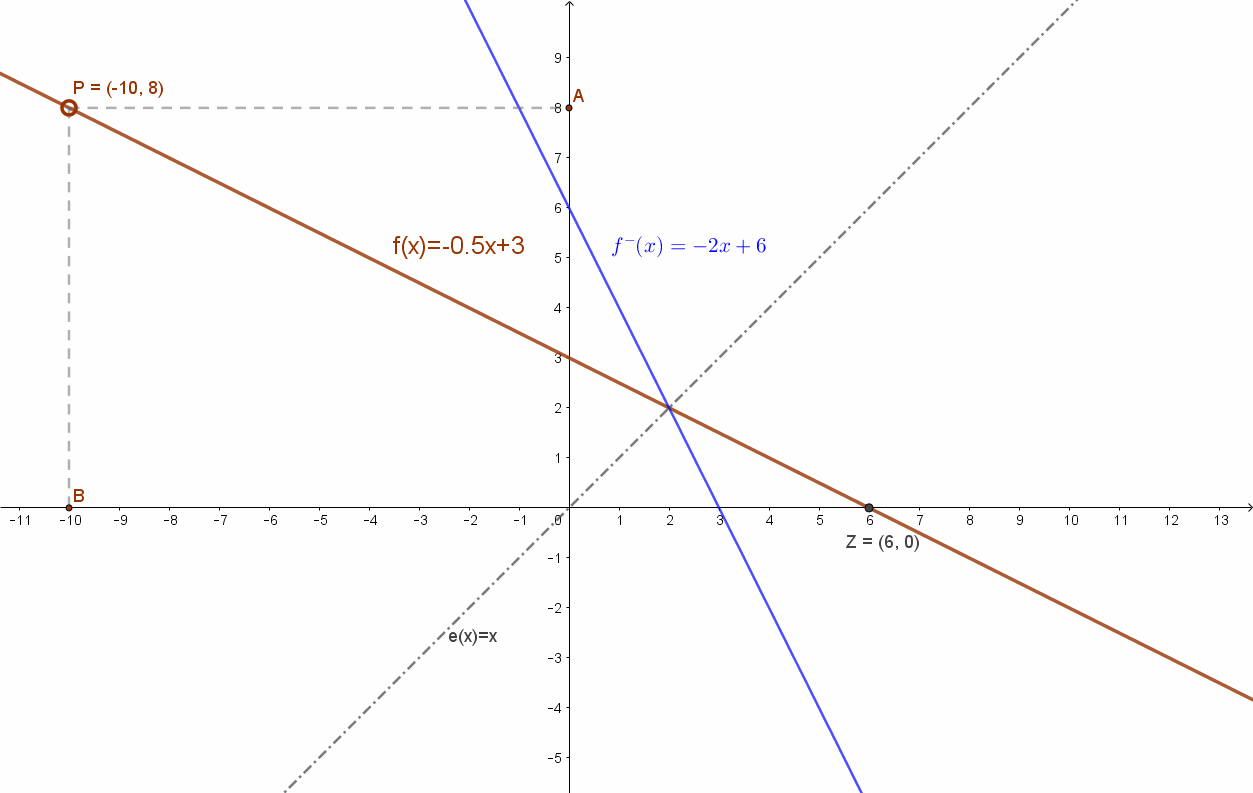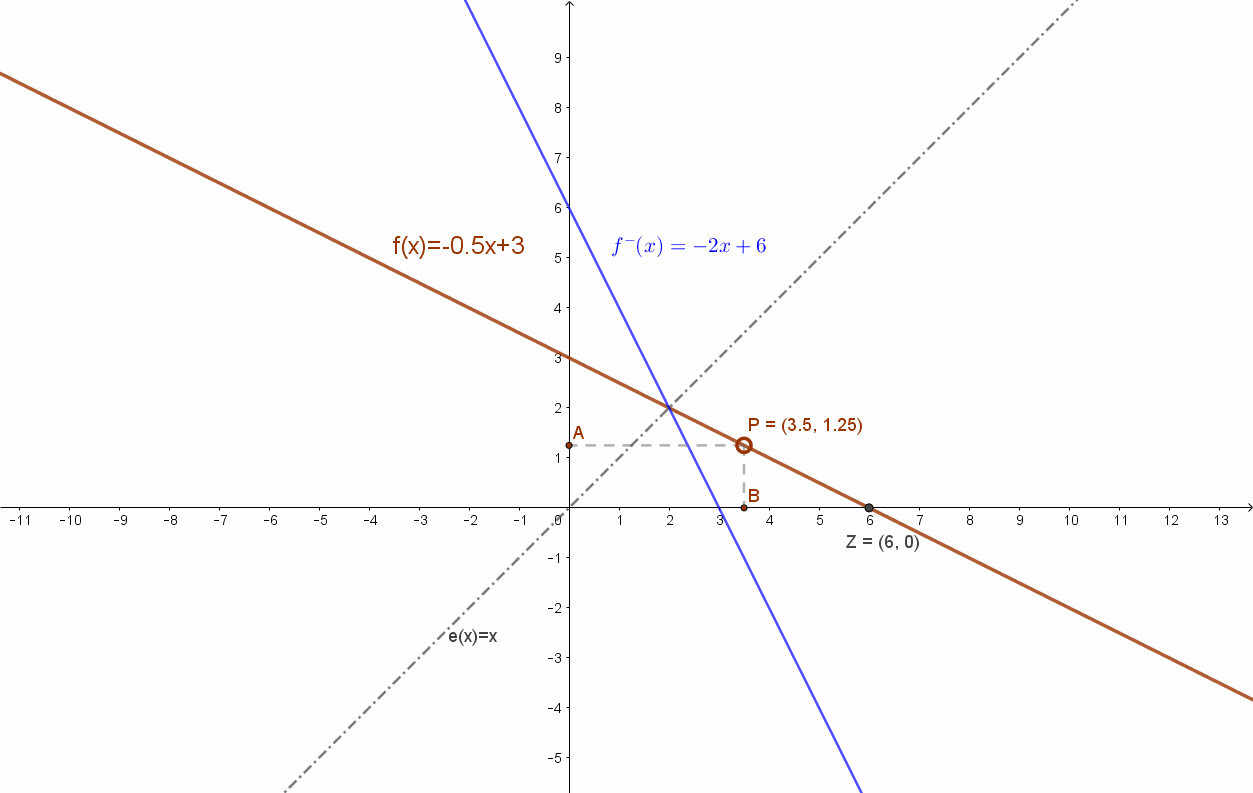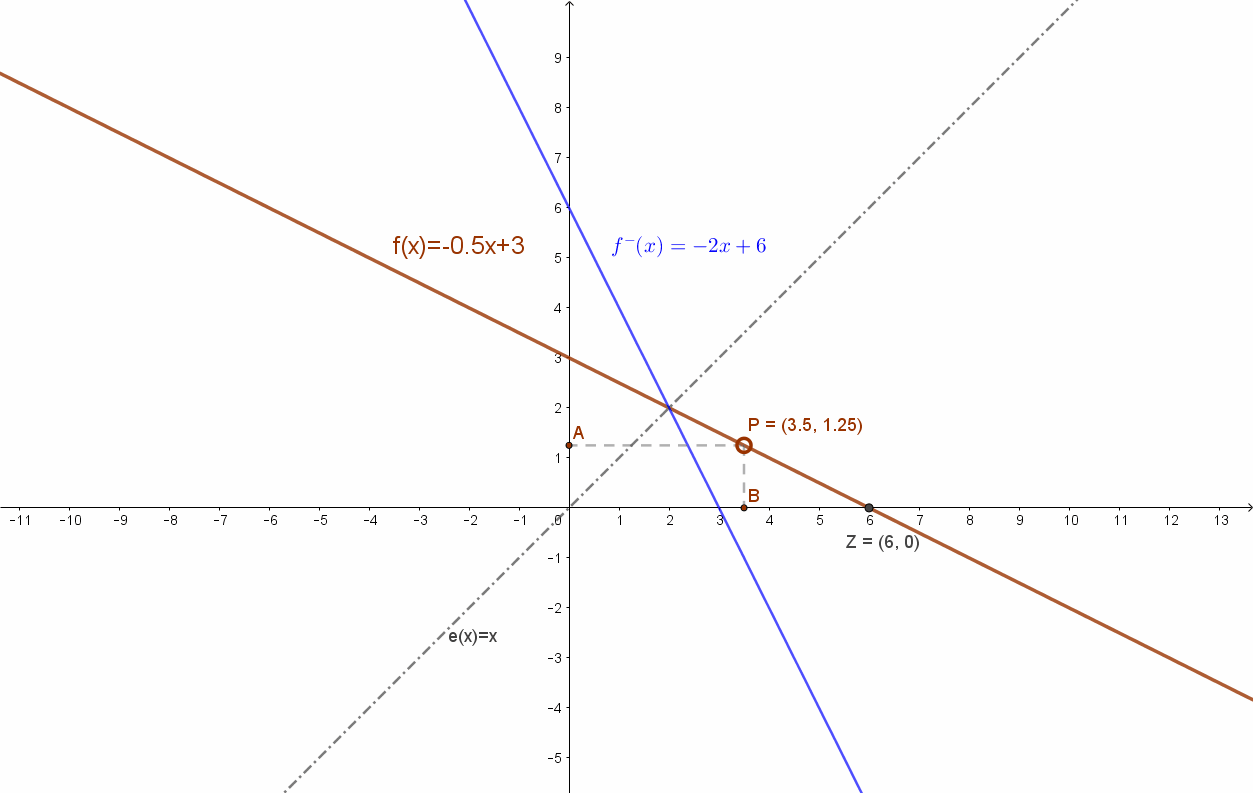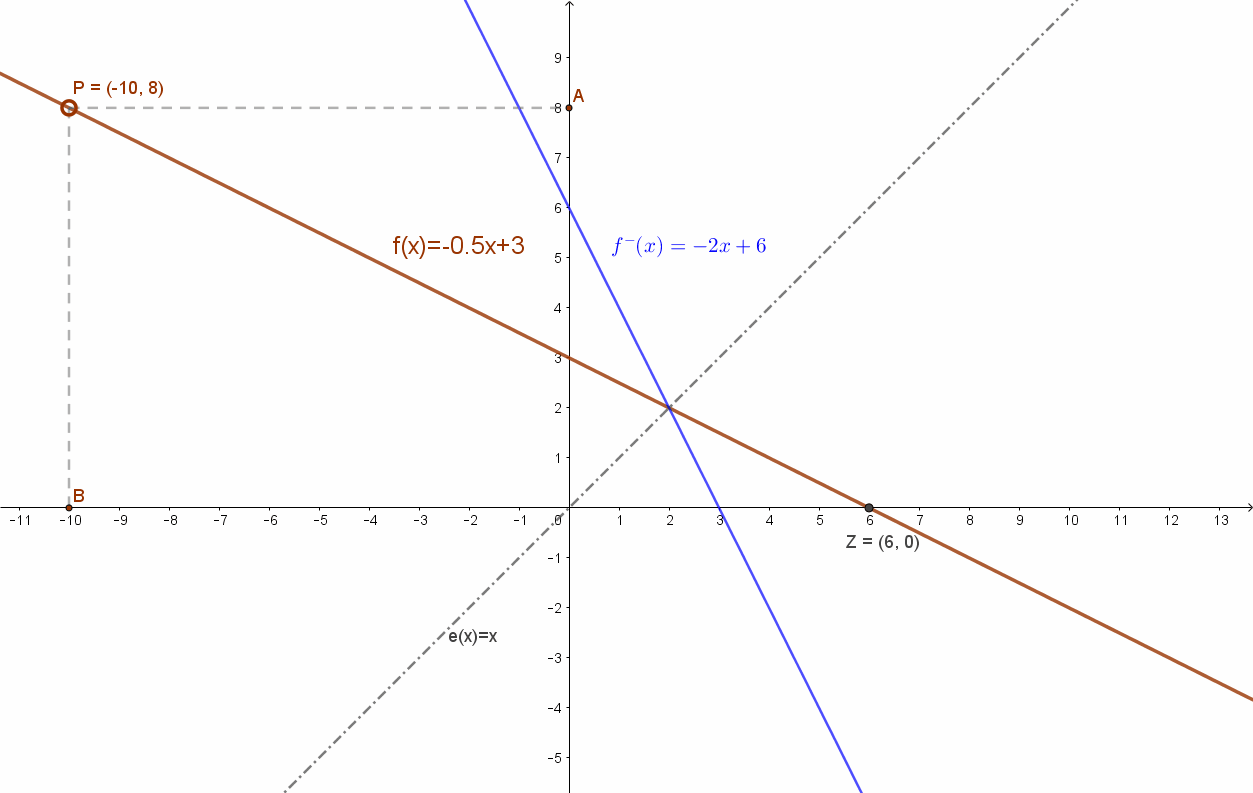
Az eredeti f(x)=-0.5x+3 függvény és az inverze, az f–(x)= -2x+6 függvények grafikonjai. Szimmetrikusak az e(x)=x egyenesre.
Megjegyzés:
Hiszen az eredeti függvény egyenletében (y=-0.5x+3) felcserélve az”x” -t az „y”-nal kapjuk. x=-0.5y+3. Ezt y-ra rendezve: y=-2x+6.
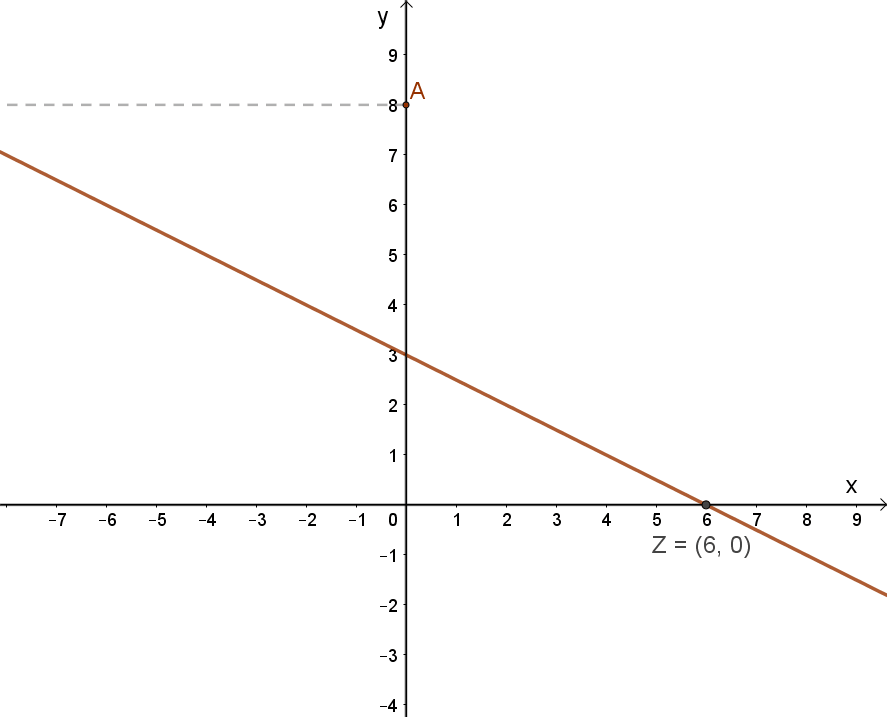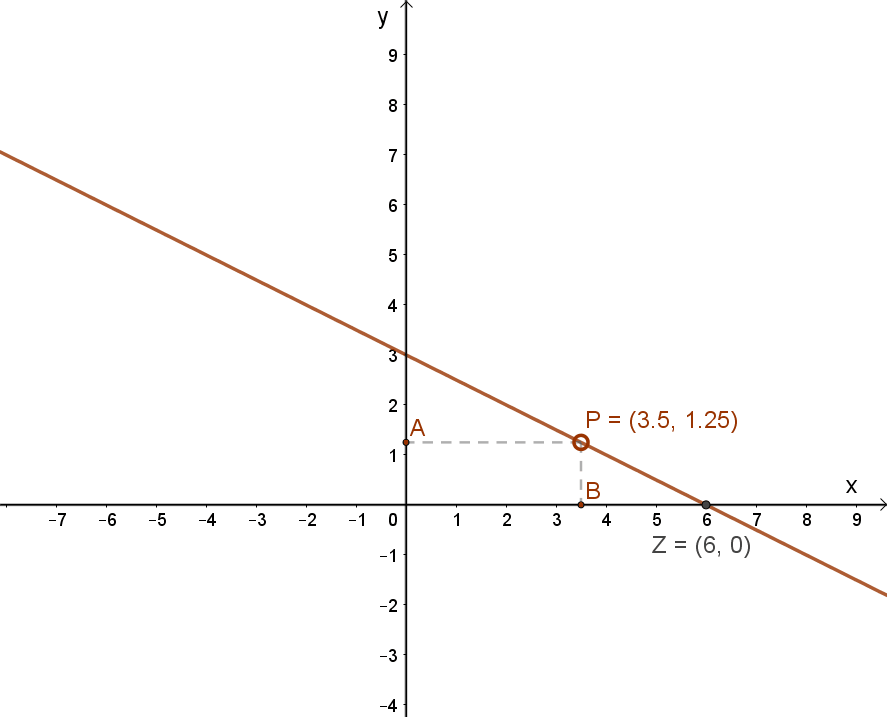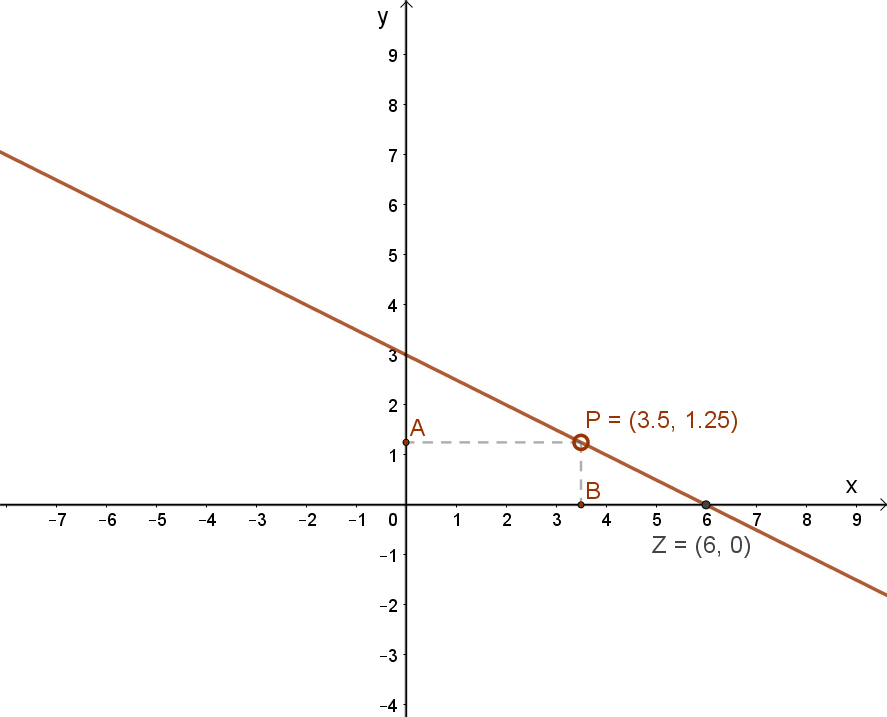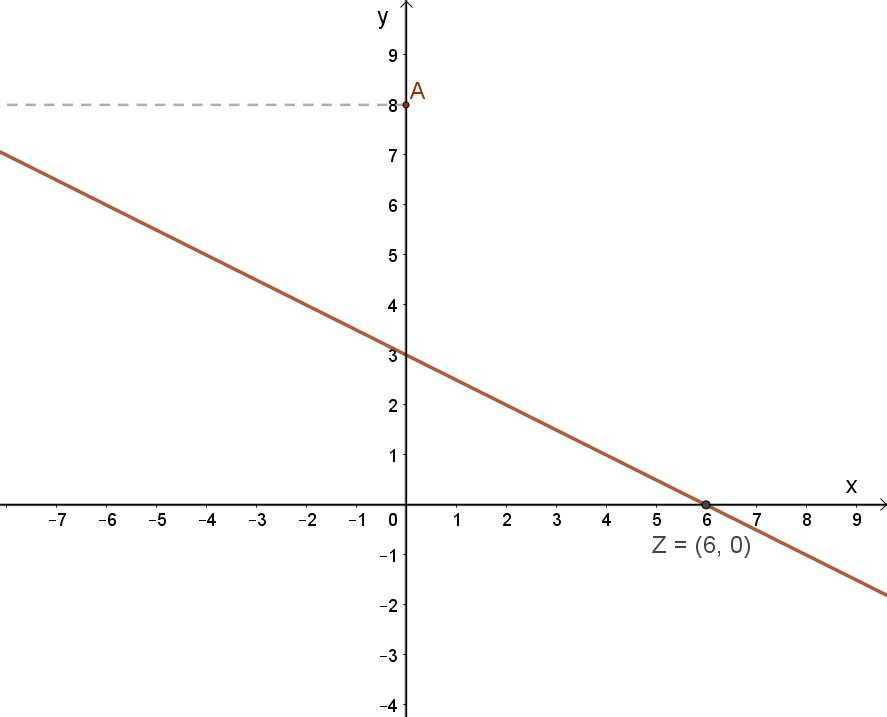


Comments are closed, but trackbacks and pingbacks are open.