A parabola egyenletének meghatározásához induljunk ki a parabola definíciójából!
Definíció:
A parabola azoknak a pontoknak az összessége (mértani helye) a síkban, amelyek a sík egy adott egyenesétől (vezéregyenes) és a sík egy adott (a vezéregyenesre nem illeszkedő) pontjától (fókusz) egyenlő távolságra vannak.
A fókuszpont és a vezéregyenes távolsága a parabola paramétere. (p).
Formulával: parabola={P|d(P,v)=d(P,F).
Nézzük azt a parabolát, amely úgy helyezkedik el a derékszögű koordináta rendszerben, hogy a parabola tengelye az y tengely (ordinátatengely), tengelypontja pedig a koordinátarendszer kezdőpontja az origó és a parabola fókusz pontja az y tengely pozitív felére esik.
A feltétel szerint a parabola fókusza: \( F\left( 0;\frac{p}{2} \right) \), akkor a parabola vezéregyenesének (v) az egyenlete: \( y=-\frac{p}{2} \).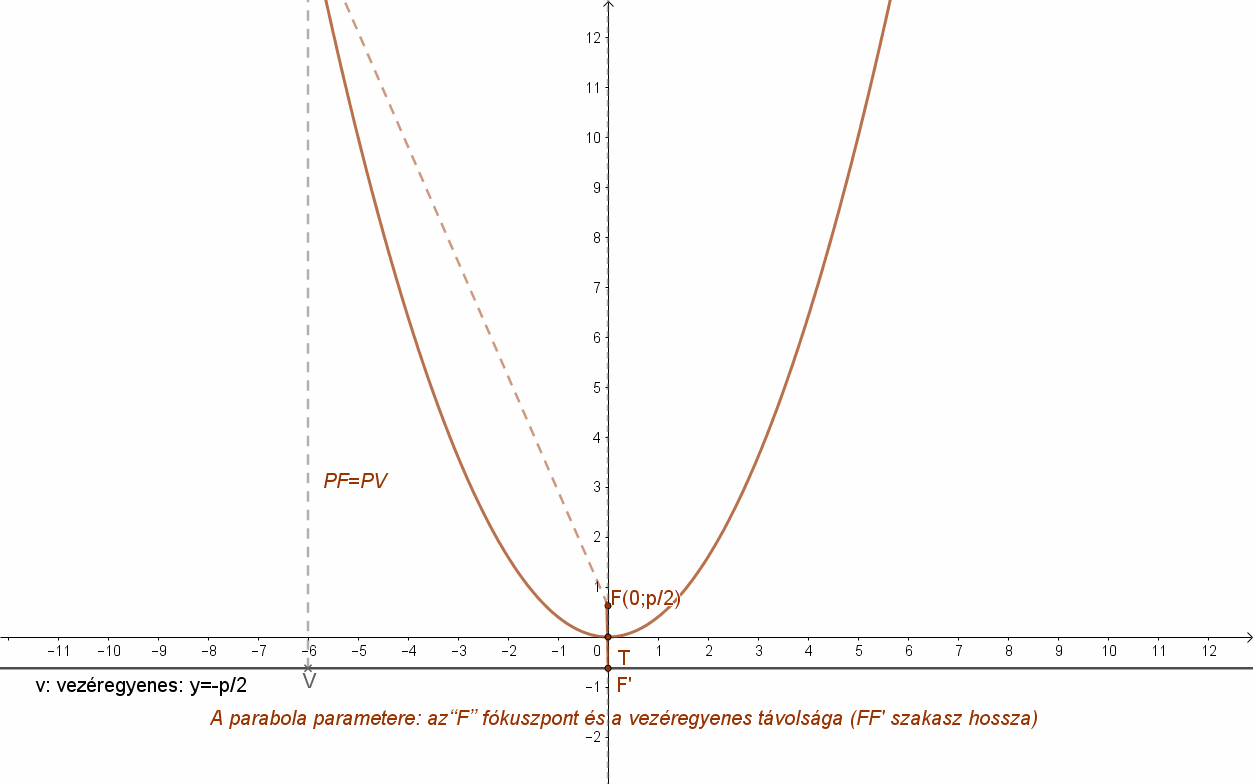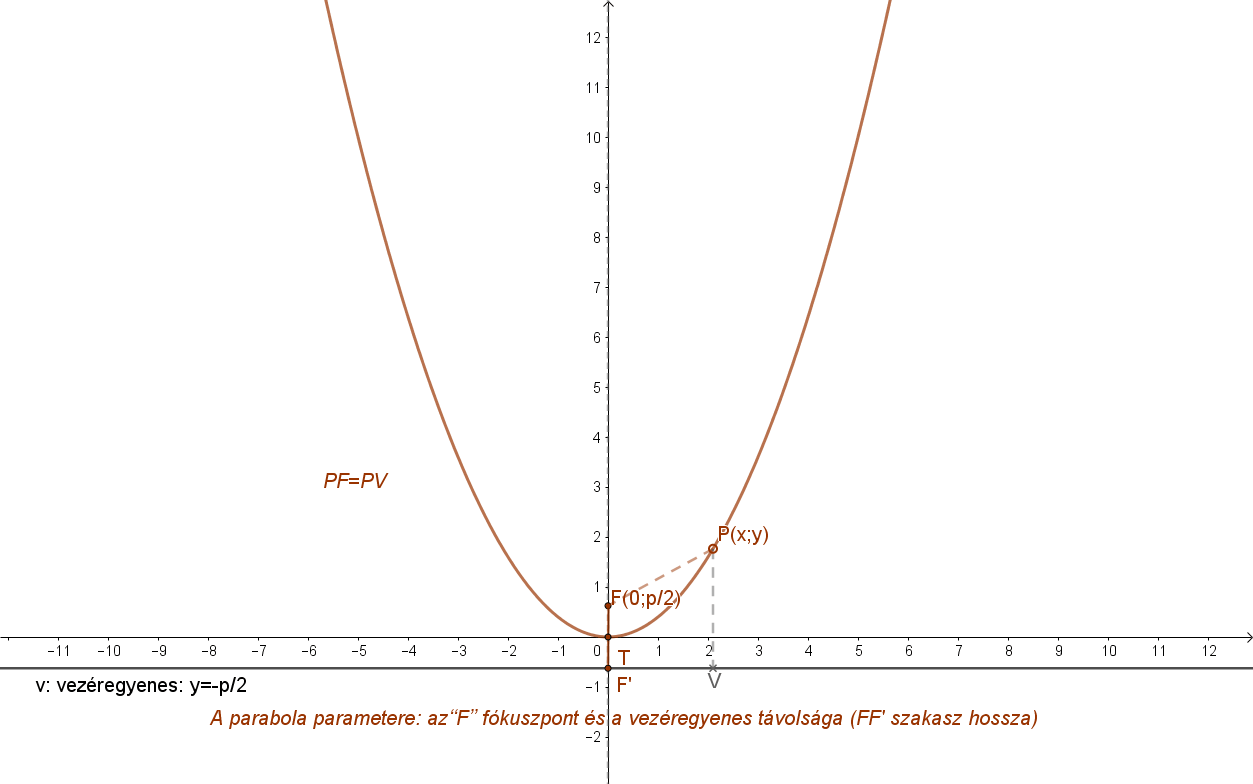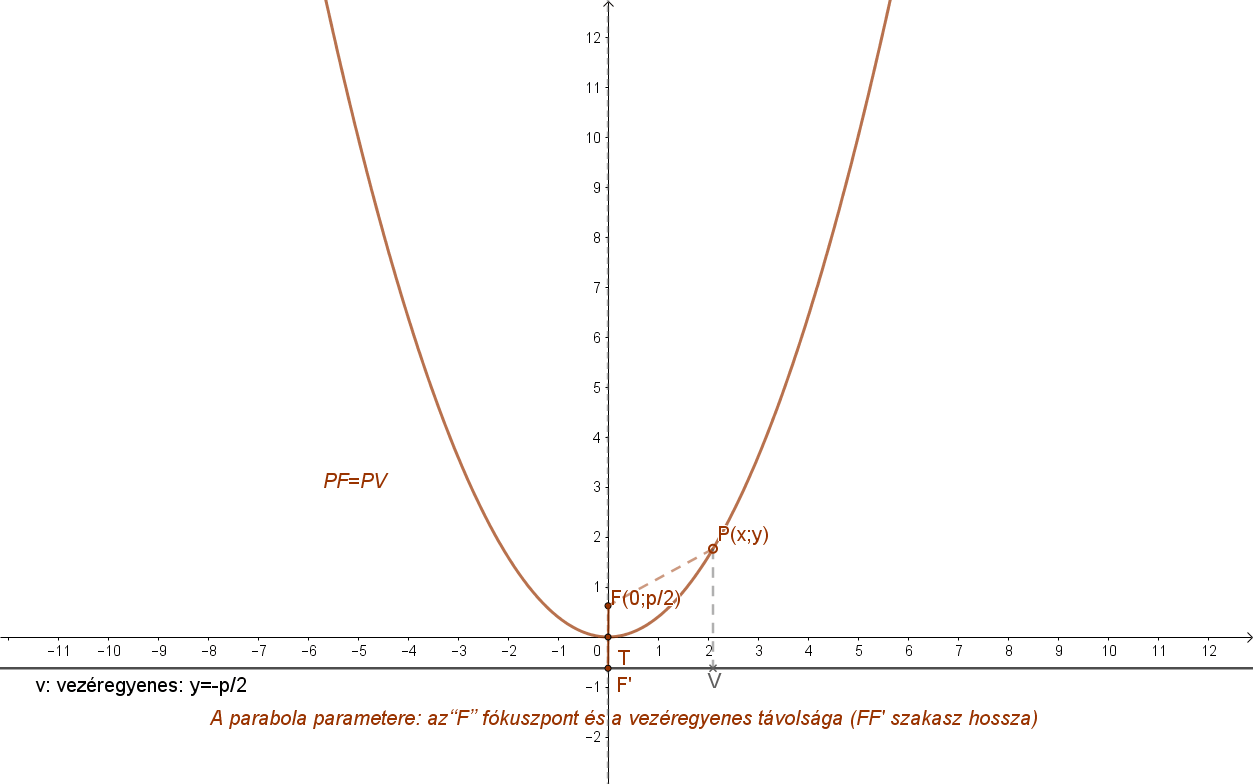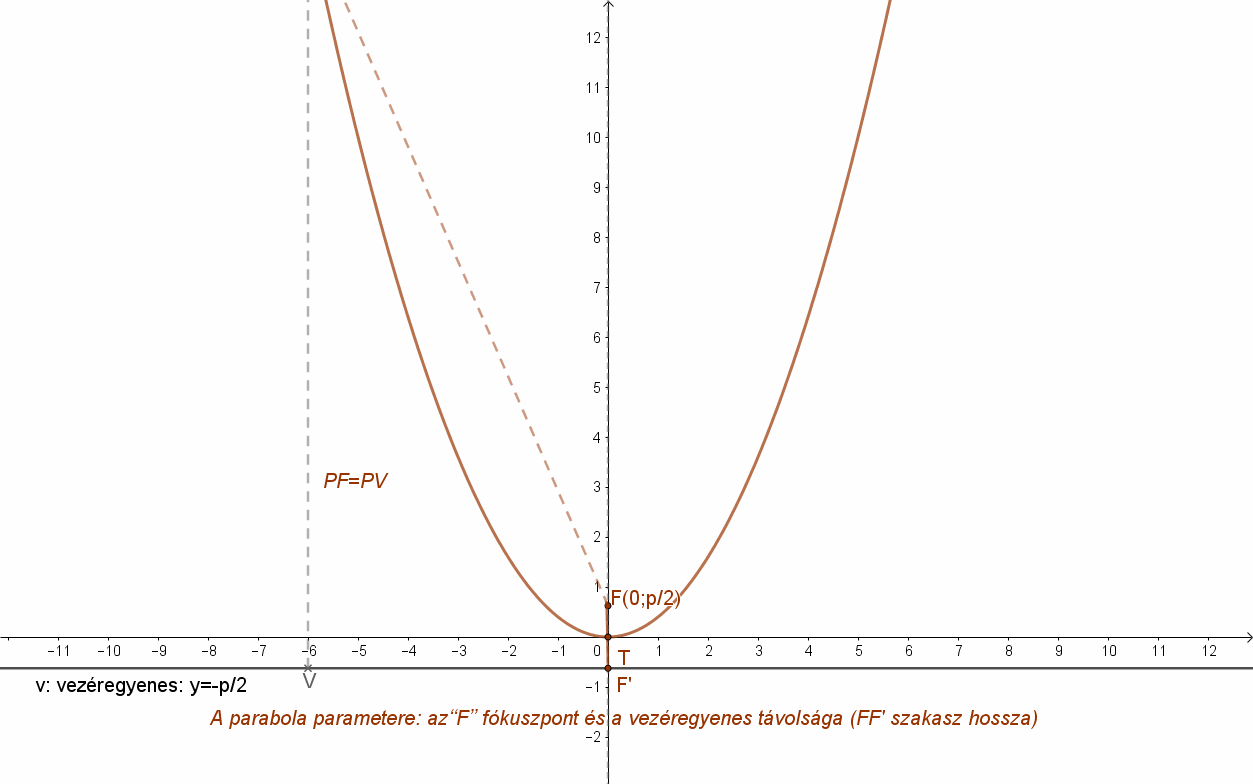
Megjegyzés:
A parabola definíciójának megfelelően fel kell írni a P pontnak a távolságát a v vezéregyenestől és a P pont távolságát az F fókusztól. Ennek a két távolságnak az egyenlőségéből kapjuk majd a parabola egyenletét.
1. P(x;y) pont távolsága a vezéregyenestől: d(P;v).
Ez a távolság két részből adódik össze:
A pontnak az x tengelytől (abszcisszatengely) való távolsága. (ez az y koordináta értéke).
Az x tengelynek a vezéregyenestől való távolsága.
Így tehát \( d(p;v)=\left|y+\frac{p}{2} \right| \), hiszen távolság nem lehet negatív.
2. P(x;y) pont távolsága a fókusztól: d(P;F).
Itt felhasználjuk a két pont távolságára tanult összefüggést: \( d(P;F)=\sqrt{x^2+\left(y-\frac{p}{2}\right)^2 } \)
A két távolságnak a parabola definíciója szerint meg kell egyeznie: d(P;v)=d(P;F).
Azaz: 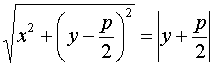
Az egyenletet négyzetre emelve:
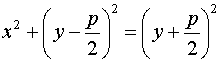
Mindkét oldalon felbontva a zárójeleket: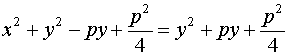
Az egyenlet mindkét oldalán megegyező tagok kiesnek: x2-py=py.
Az egyenletet rendezve: x2=2py.
És ezt kellett bizonyítani.
Kiegészítés
Ha a parabola tengelye párhuzamos az y tengellyel és tengelypontja nem az origó, hanem T(u;v) koordinátájú pont, akkor a parabola egyenlete: \( y=\frac{1}{2p}(x-u)^2+v \).
Legyen például a parabola paramétere: p=2, a tengelypontja: T(3;-1).
Így fókusza: F(3;0), egyenlete: \( y=\frac{1}{4}(x-3)^2-1 \). Ennek grafikonja:
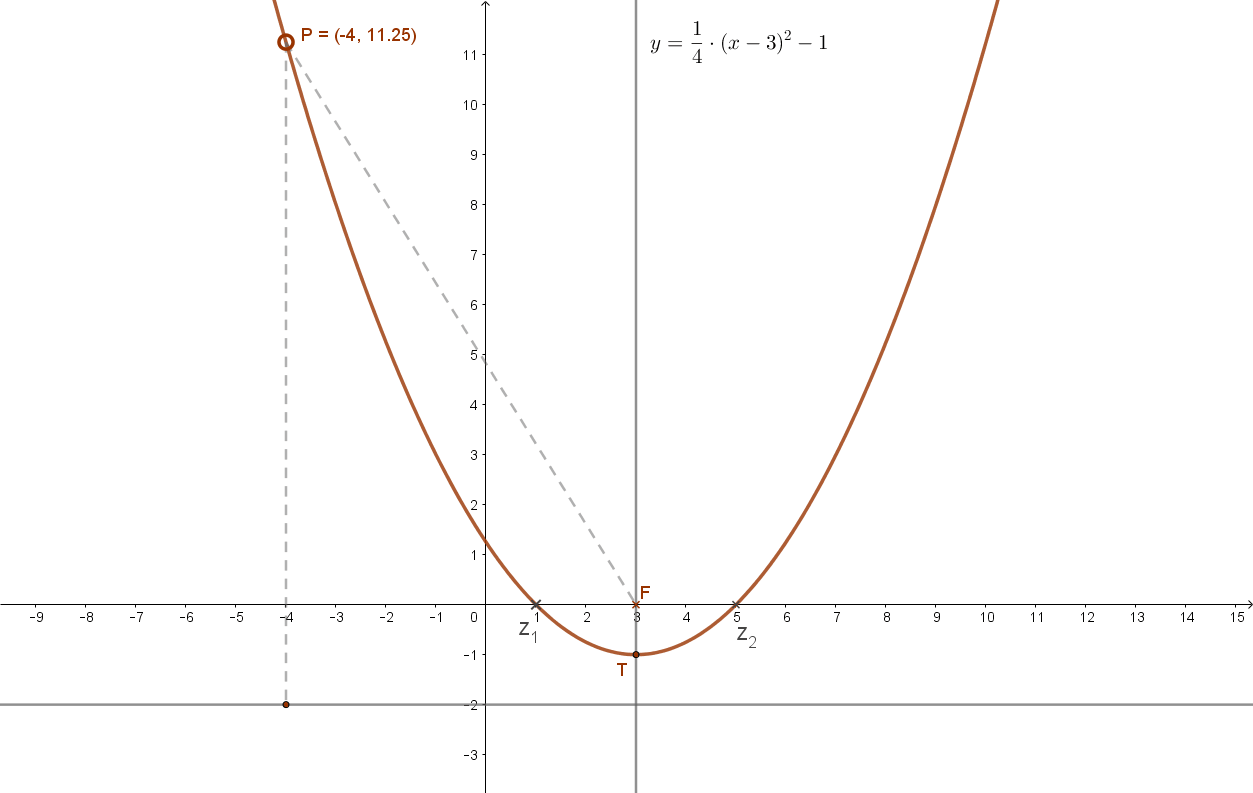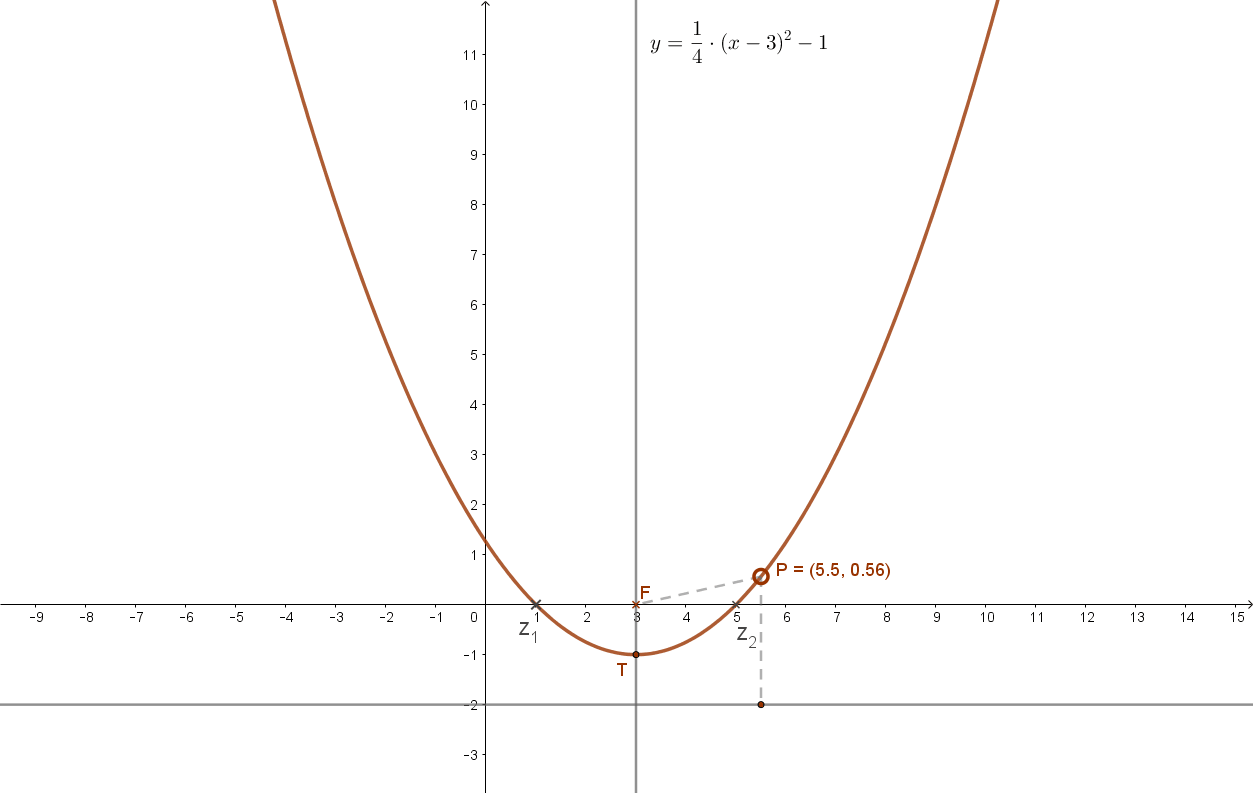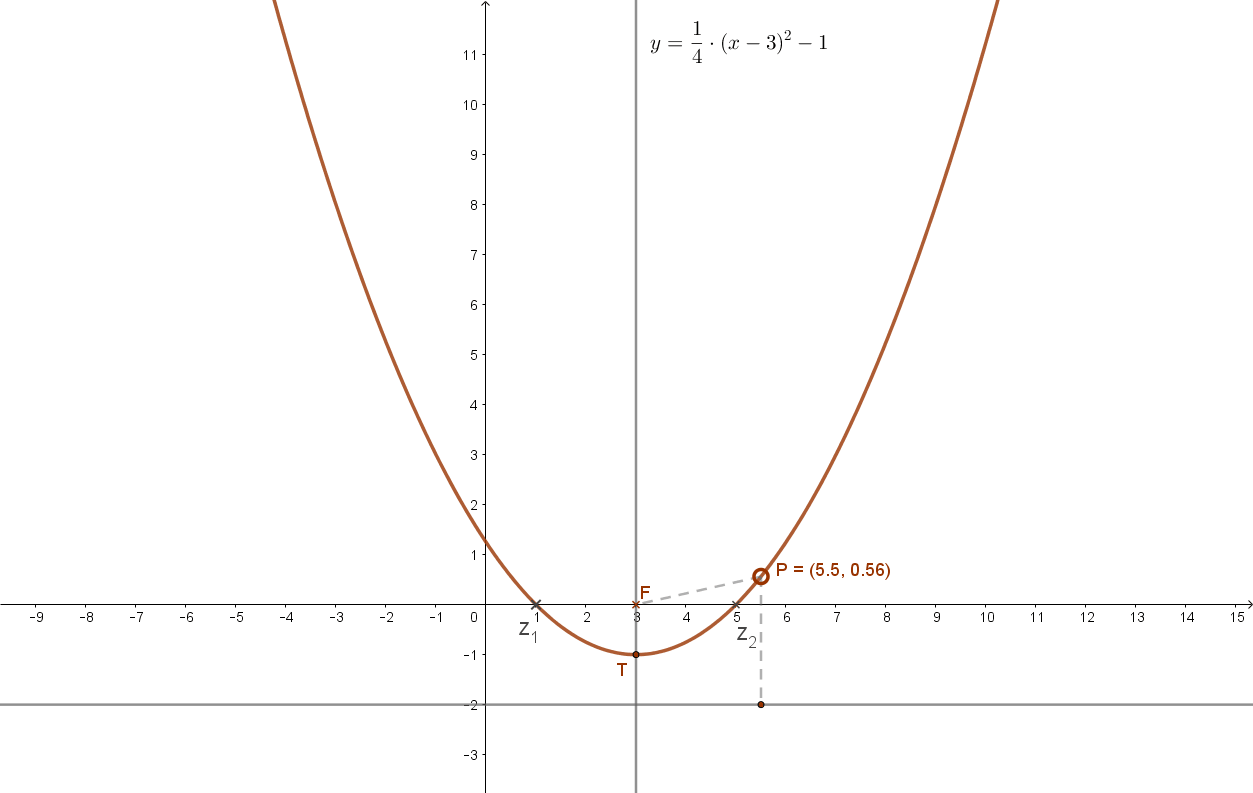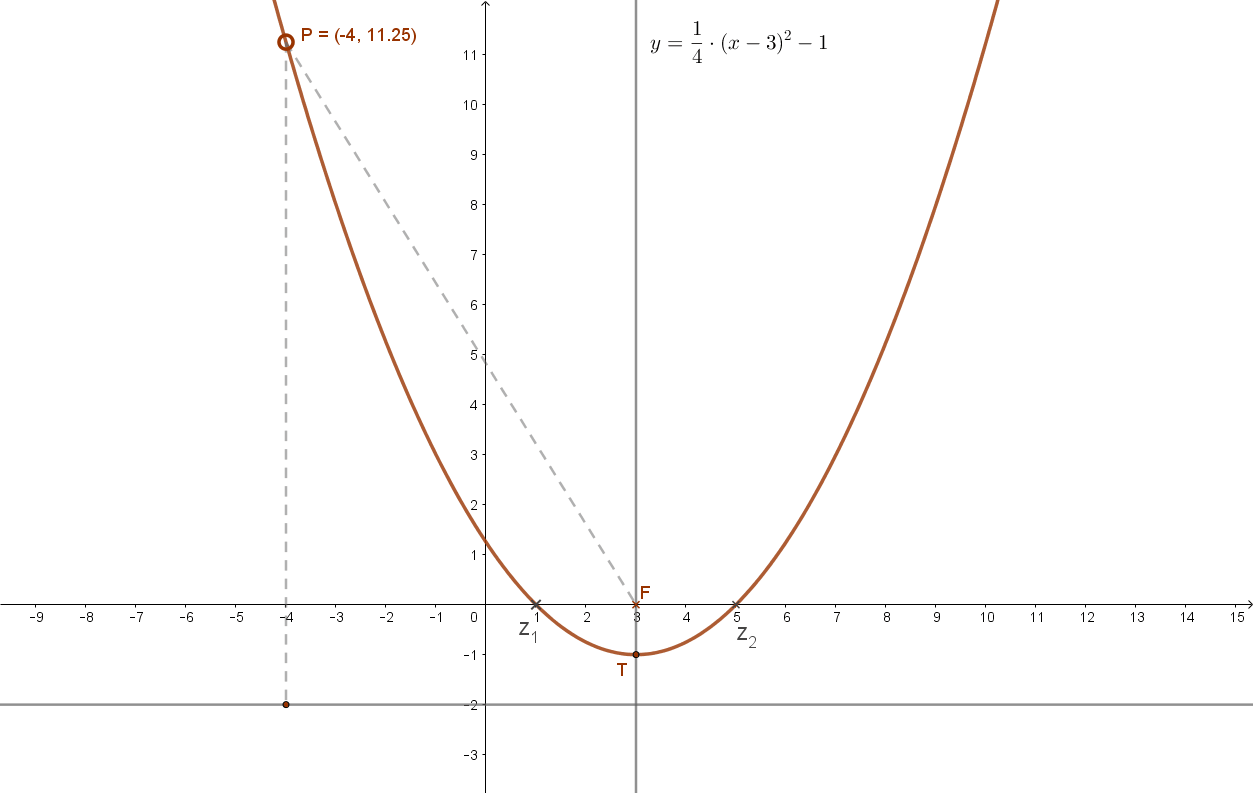
Megjegyzés:
Szokás a fenti egyenletet y-ra rendezve a következő alakba írni: \( y=\frac{1}{2p}x^2 \). Itt az \( \frac{1}{2p} \) együtthatóból a parabola meredeksége következik.
Nézzük most a legegyszerűbb másodfokú függvényt, az f(x)=x2 függvény grafikonjának az egyenletét. Ez y=x2 alakú.
A mellékelt ábrán az y=x2 egyenletű parabolát láthatjuk.
Ennek a parabolának a paraméterére a fentiek értelmében a következőt kapjuk: \( \frac{1}{2p}=1 \). Ebből pedig \( p=\frac{1}{2} \).
Így a fókuszpont koordinátái: \( F\left( 0;\frac{1}{4} \right) \).
Ezen parabola vezéregyenesének egyenlete: \( y=-\frac{1}{4} \).
Feladat:
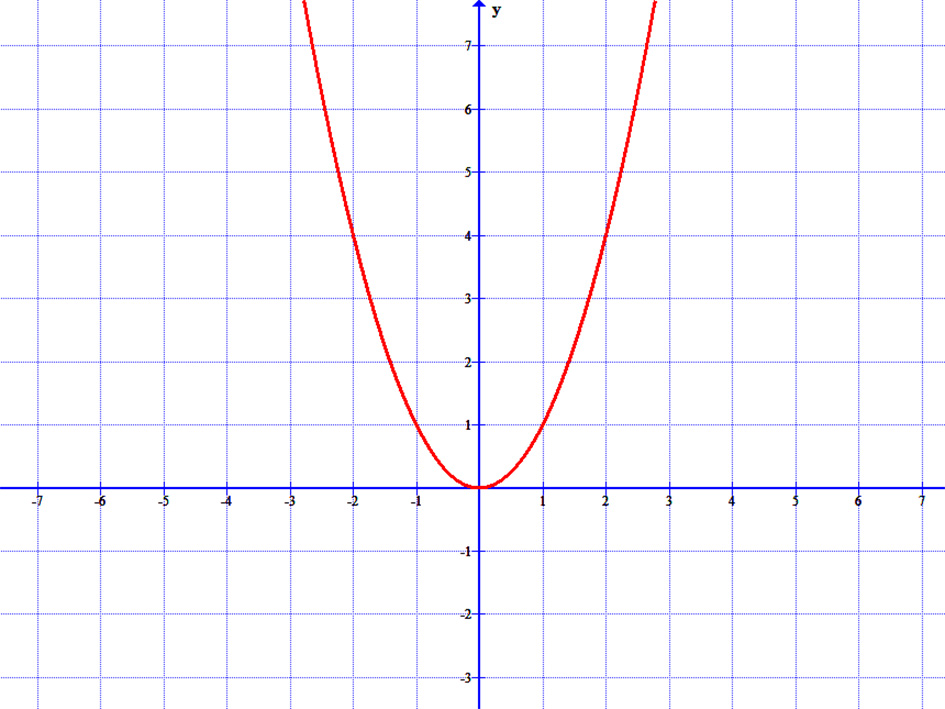
Írja fel annak a parabolának az egyenletét, amelynek tengelye az y tengely, tengelypontja az origó és fókusza a (0;3) pont.
(Összefoglaló feladatgyűjtemény 3398. feladat.)
Megoldás:
A feltételeknek megfelelő helyzetű p paraméterű parabola fókusza: \( F\left( 0;\frac{p}{2} \right) \).
A feltétel szerint viszont F(0;3). Ebből p=6 következik.
Így a parabola általános \( y=\frac{1}{2p}·x^2 \) egyenletét felhasználva: \( y=\frac{1}{12}·x^2 \) adódik.
Ennek grafikonja:
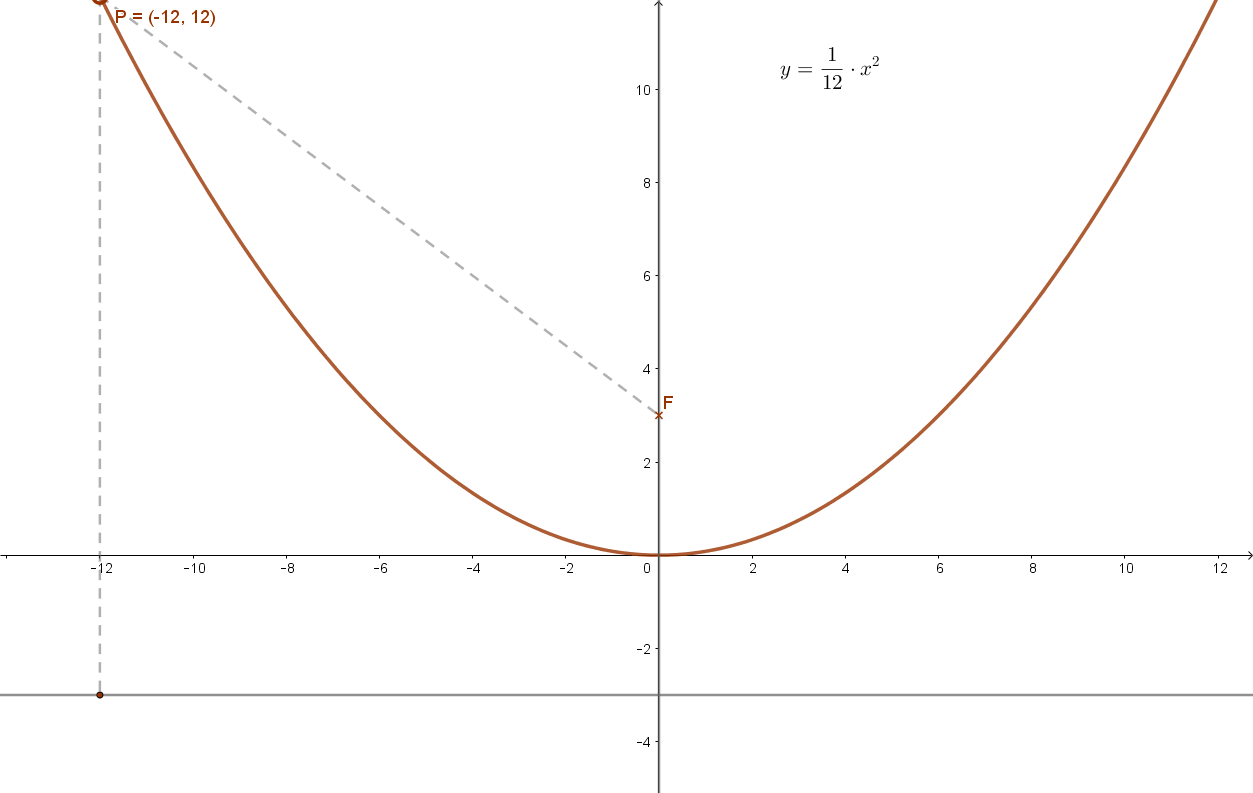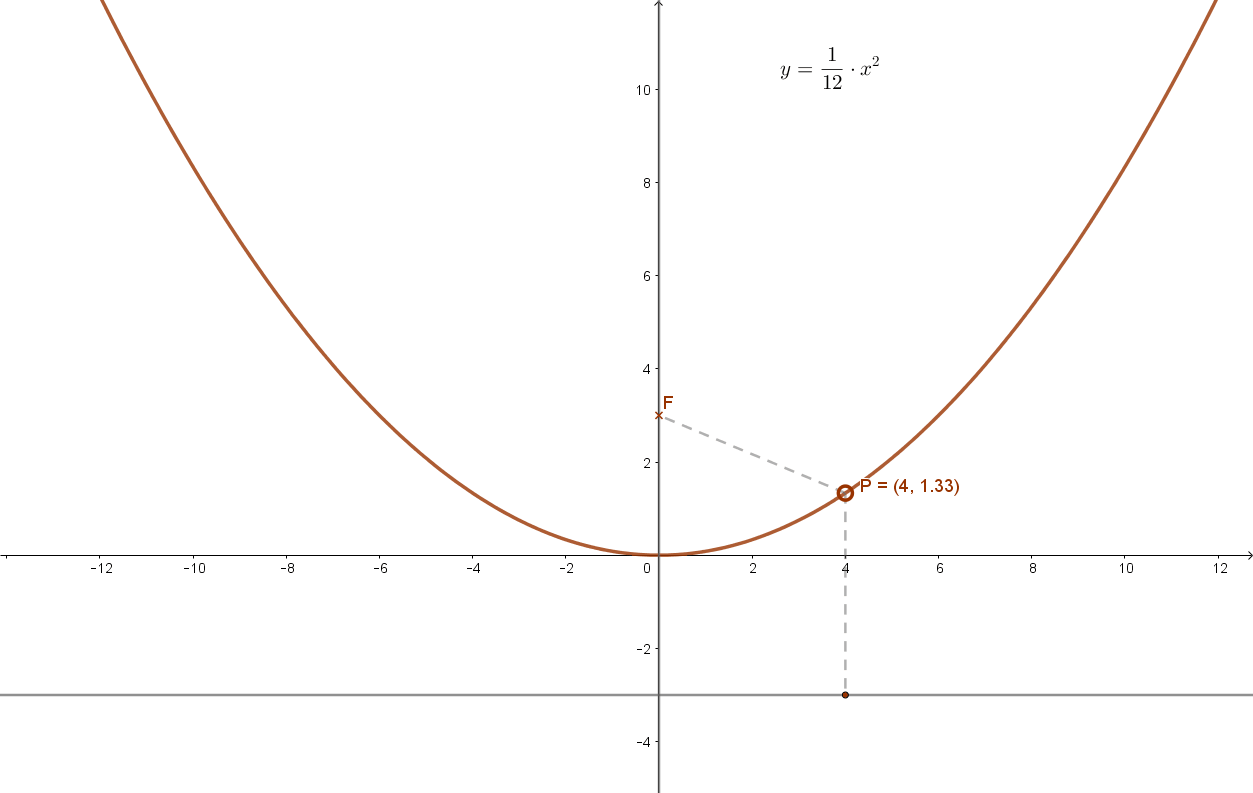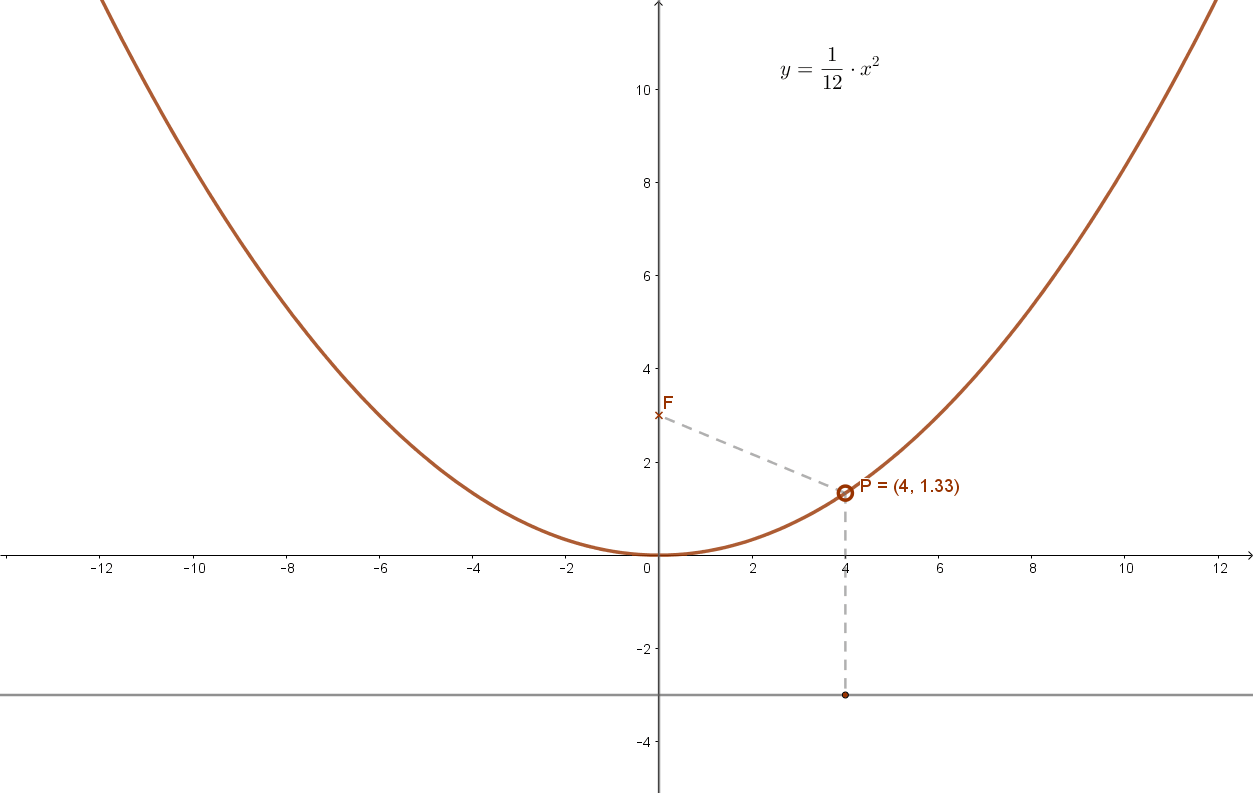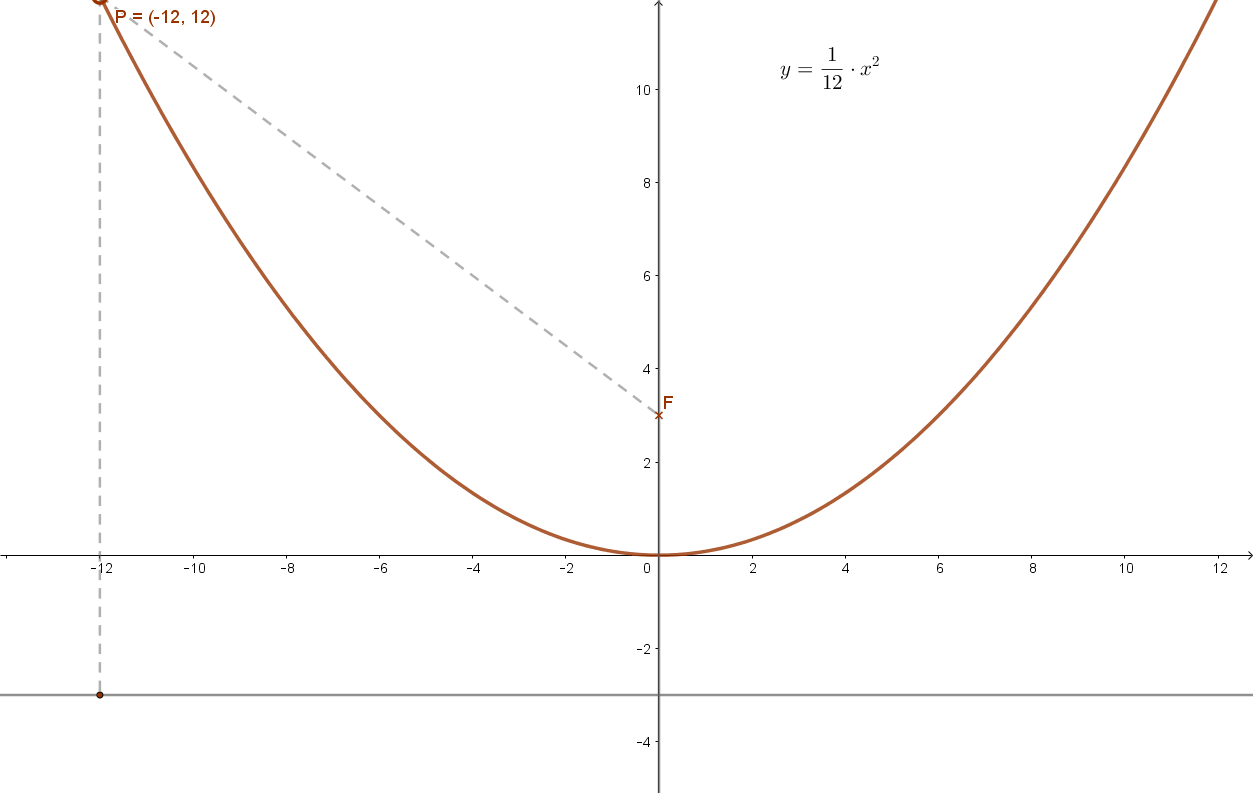


Comments are closed, but trackbacks and pingbacks are open.