Definíció:
A parabola azoknak a pontoknak az összessége (mértani helye) a síkban, amelyek a sík egy adott egyenesétől (vezéregyenes) és a sík egy adott (a vezéregyenesre nem illeszkedő) pontjától (fókusz) egyenlő távolságra vannak.
Formulával: parabola={P|d(P,v)=d(P,F)}.
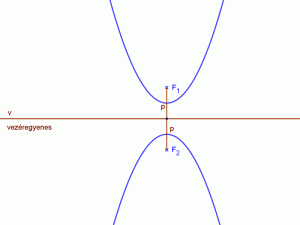
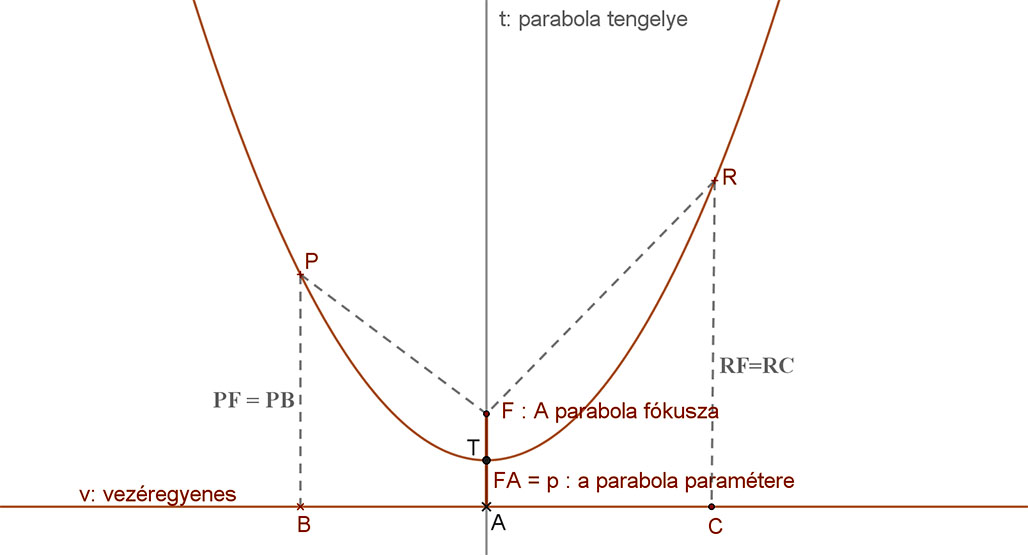A mellékelt ábra jelölései szerint:
v: vezéregyenes, F: fókuszpont.
p: fókuszpont és vezéregyenes távolsága, a parabola paramétere.
P: a parabola egy tetszőleges pontja.
t: a parabola tengelye.
T: a parabola tengelypontja.
A parabolát adott fókuszpont és adott vezéregyenes egyértelműen meghatározza.
Az alábbi animáció esetén a fókuszpont és a vezéregyenes távolsága, a parabola paramétere: FF’= 1.25, azaz 5/4.
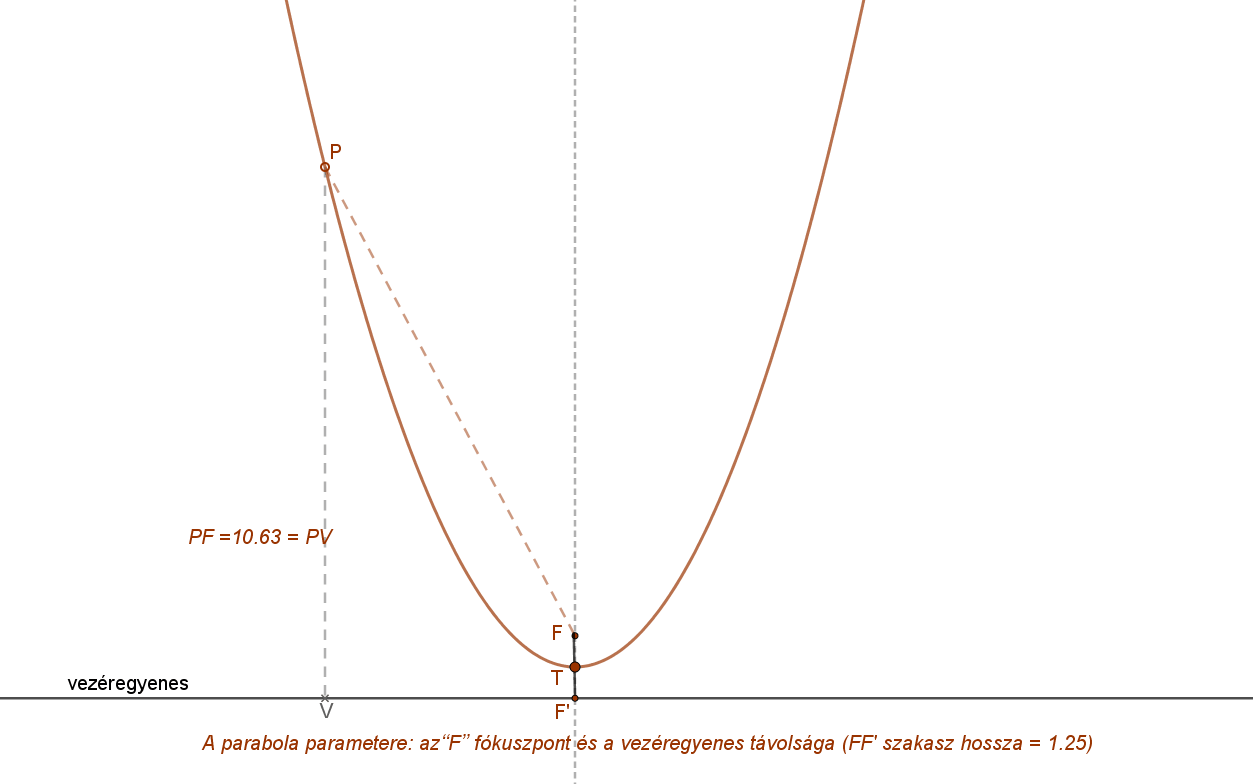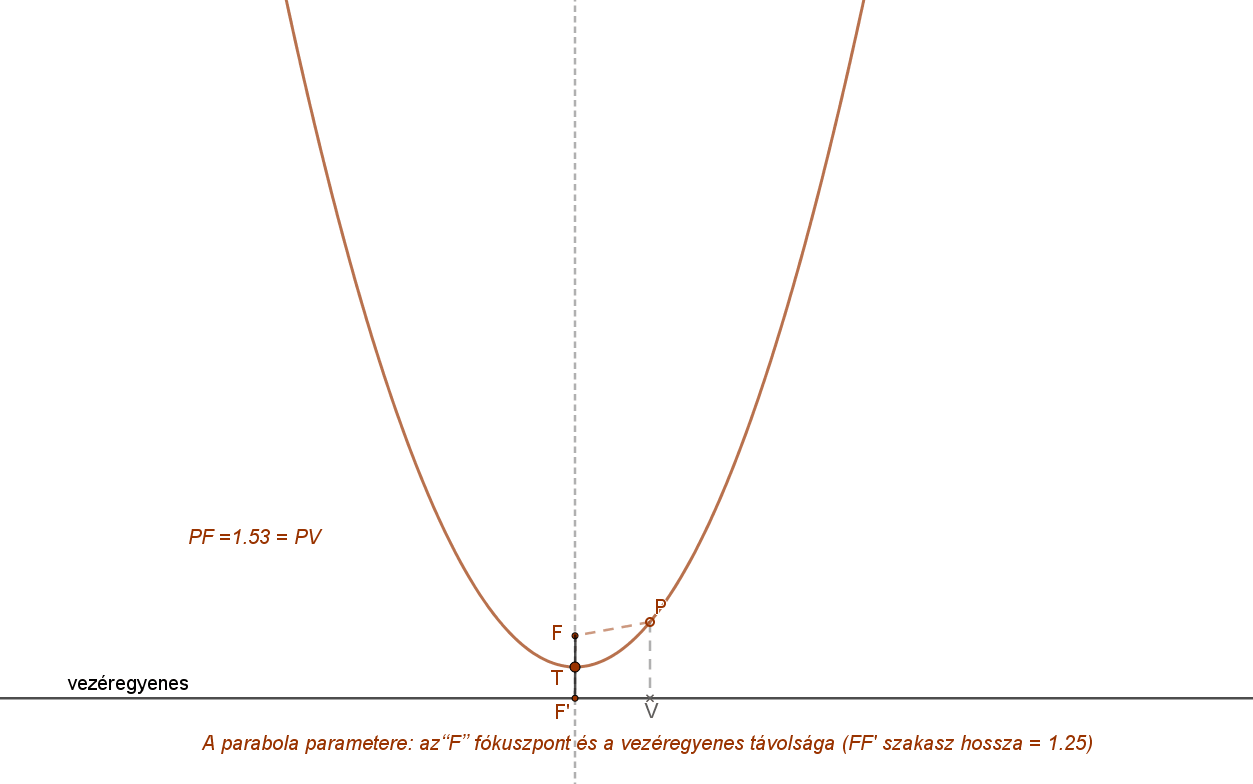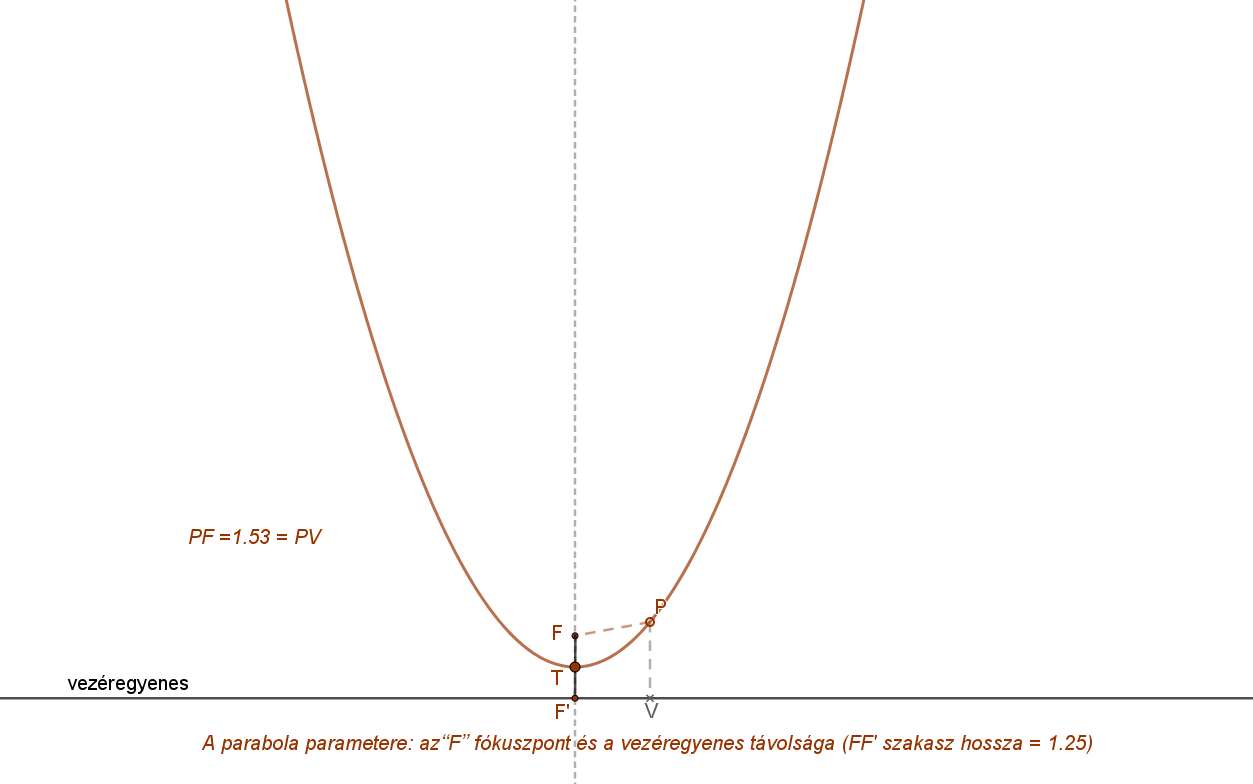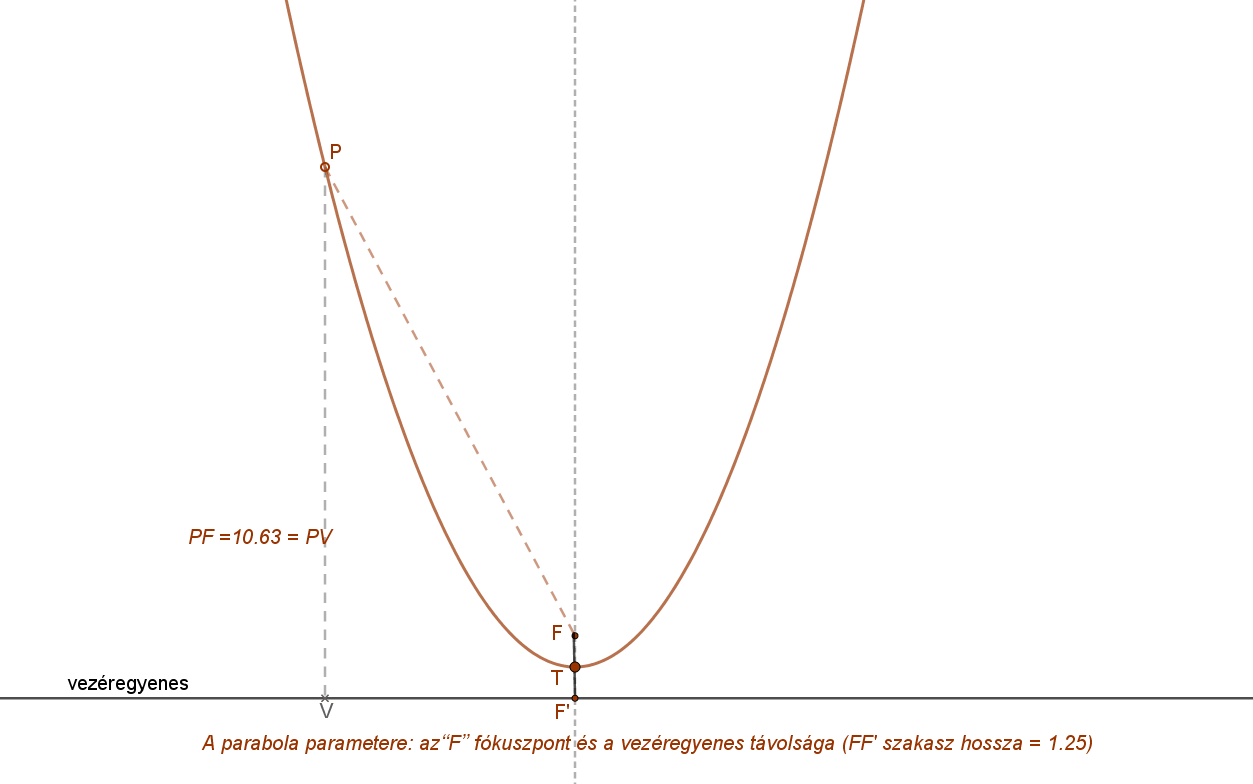
Adott vezéregyenes mellett egy adott paraméter érték azonban nem egyértelmű definíció.
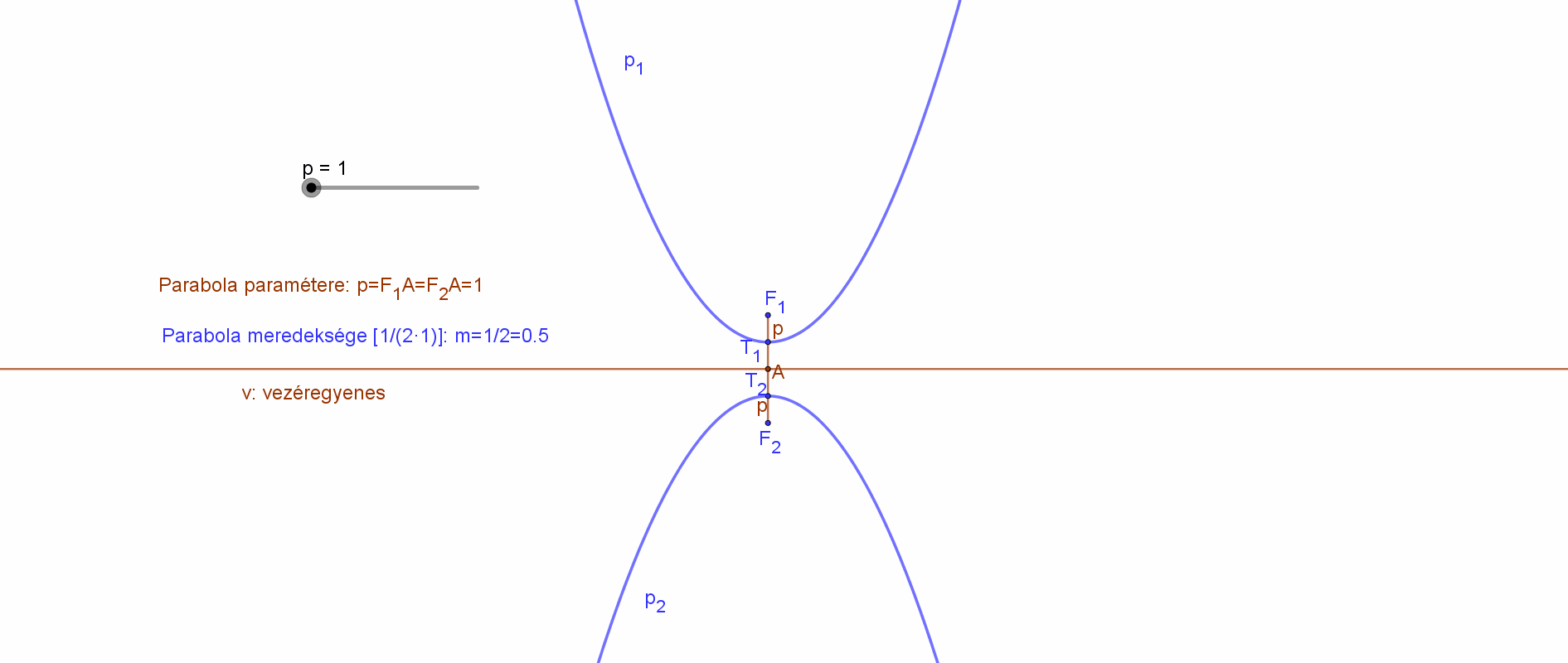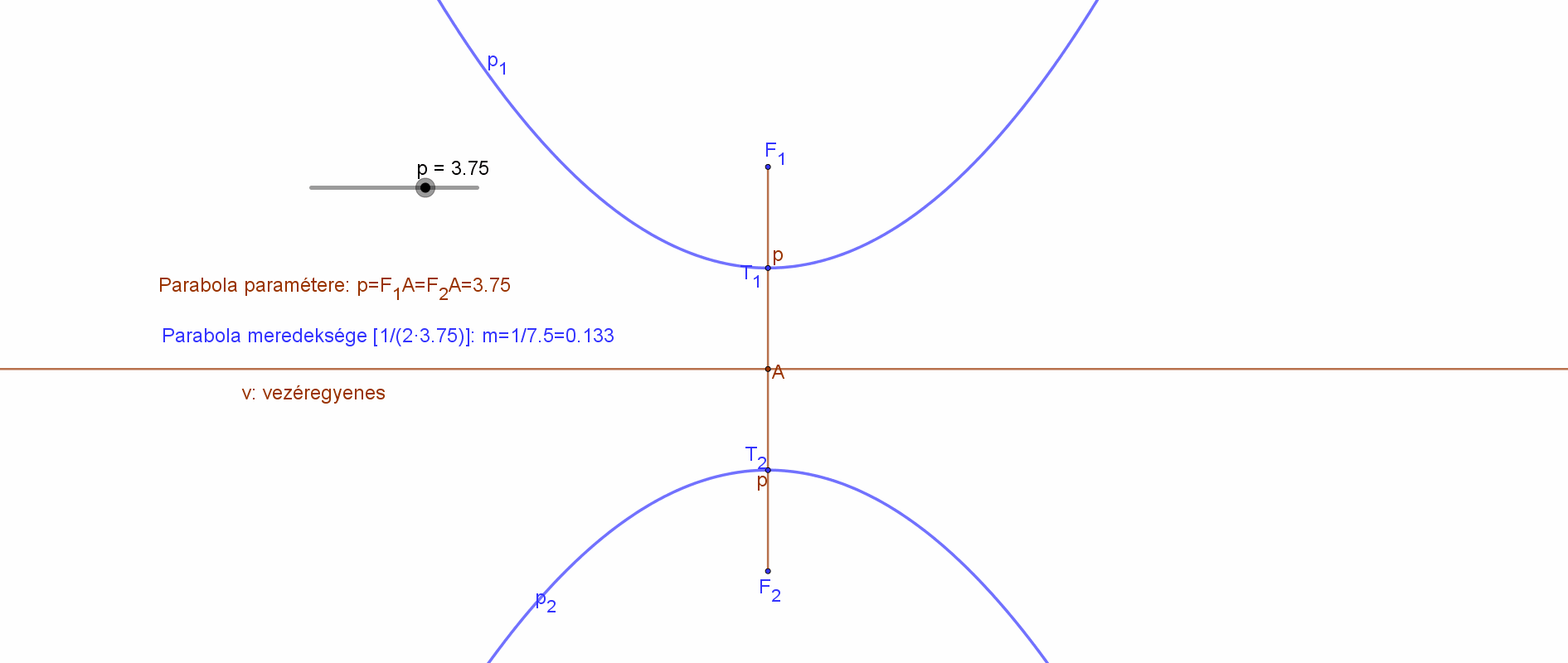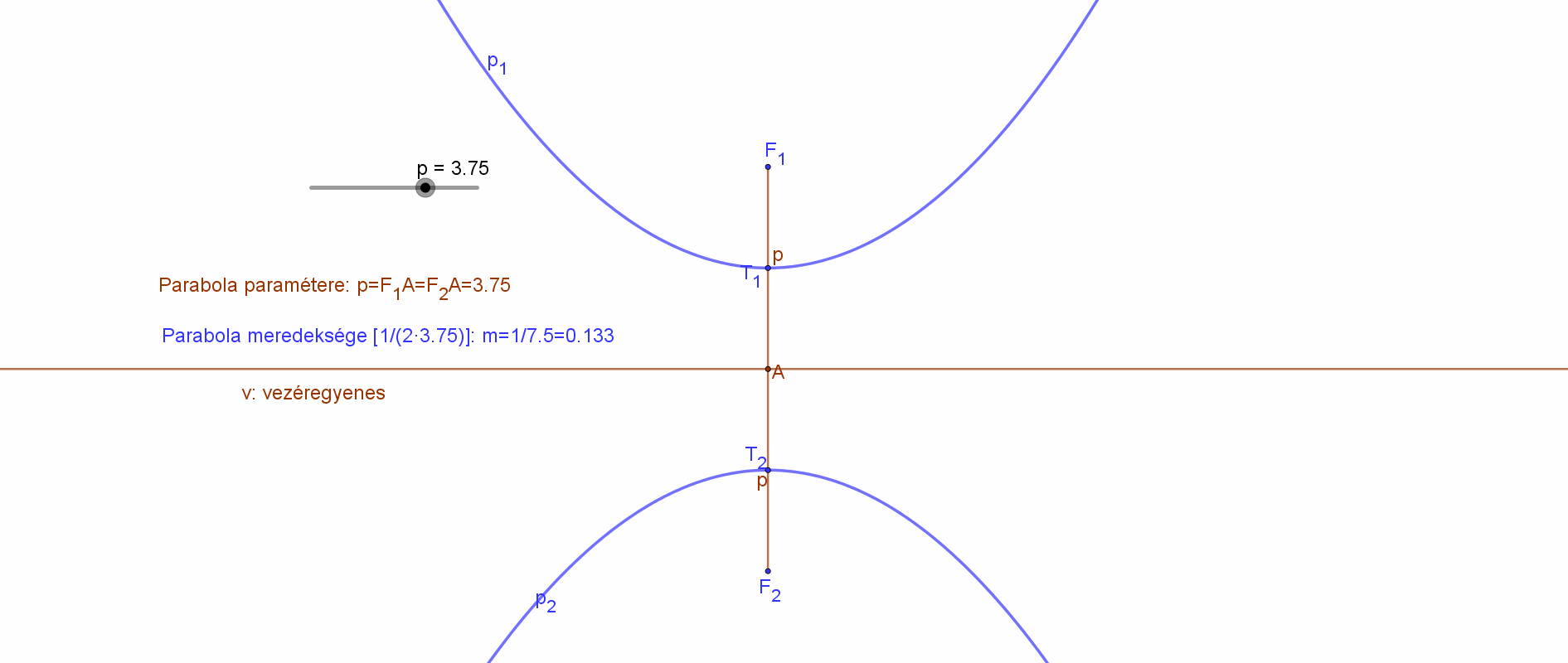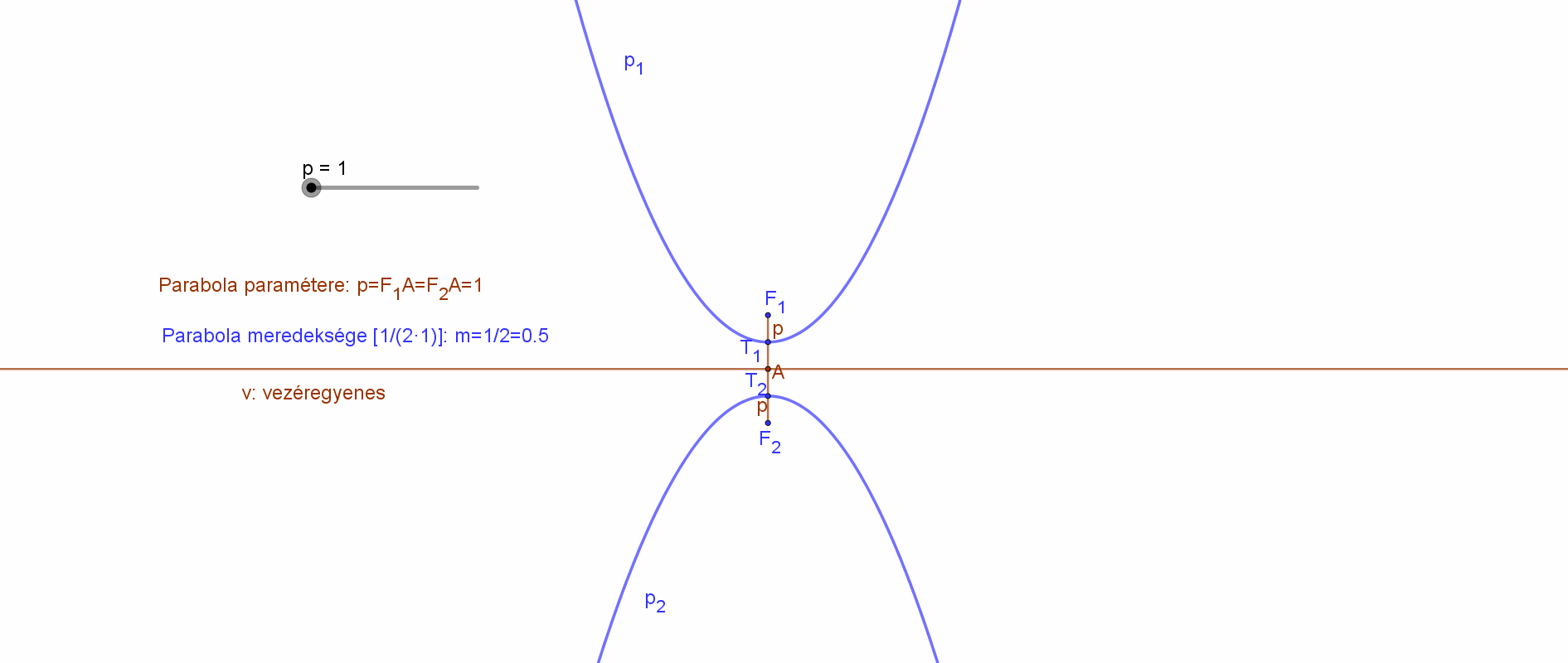
Hiszen a paraméter egy távolság, amely pozitív érték. Így ebben az esetben két parabola (két fókuszpont) is megfelel az adott vezéregyeneshez és a megadott paraméterhez. A parabola fókusza lehet a vezéregyenes egyik vagy másik oldalán. A két parabola így tengelyesen szimmetrikus a vezéregyenesre.
Az alábbi animáció azt mutatja, hogyan függ a parabola (azaz a fókuszpont) vezéregyeneshez viszonyított helyzete és a parabola meredeksége a paraméter függvényében.
A parabola vonala euklideszi értelemben nem szerkeszthető, de véges számú pontja igen. Legyen adott a parabola vezéregyenese és fókusza.
Ennek birtokában a következőképpen végezhetjük el a parabola egy-egy pontjának a szerkesztését: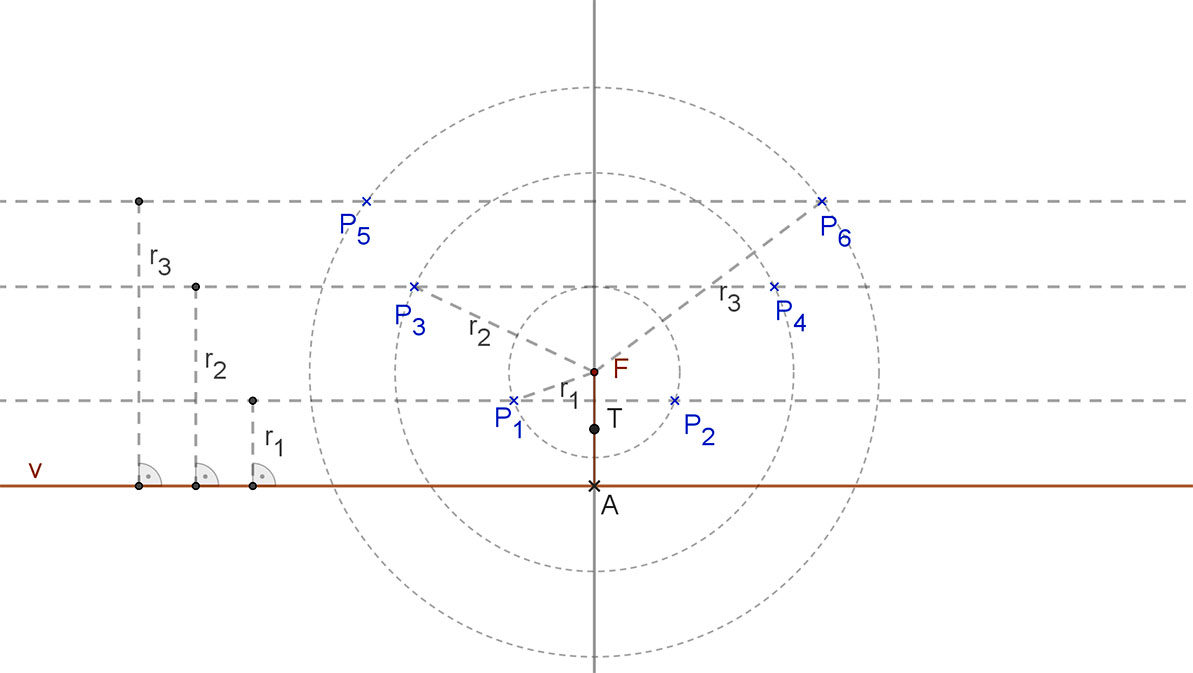
A parabola T tengelypontjának szerkesztése a legegyszerűbb, hiszen az F fókusz és a v vezéregyenes távolságának a felező pontja.
A parabola további pontjainak a fókusztól és a vezéregyenestől való távolsága már nagyobb kell legyen, mint a parabola p paraméterének a fele.
A parabola további pontjainak a fókusztól és a vezéregyenestől való távolsága már nagyobb kell legyen, mint a parabola p paraméterének a fele.
Legyenek ezek a távolságok r1, r2, r3, stb. Az F fókusztól ilyen távolságra lévő pontok összessége a fókusz körül az adott távolsággal húzott körív.
A v vezéregyenestől ezen távolságra lévő pontok összessége a vezéregyenessel az adott távolságban húzott párhuzamos egyenesek.
Ahol a párhuzamosok a köríveket metszik, azok lesznek a parabola pontjai. (r1 távolság esetén P1, P2, r2 távolság esetén P3, P4 és r3 távolsággal P5, P6.
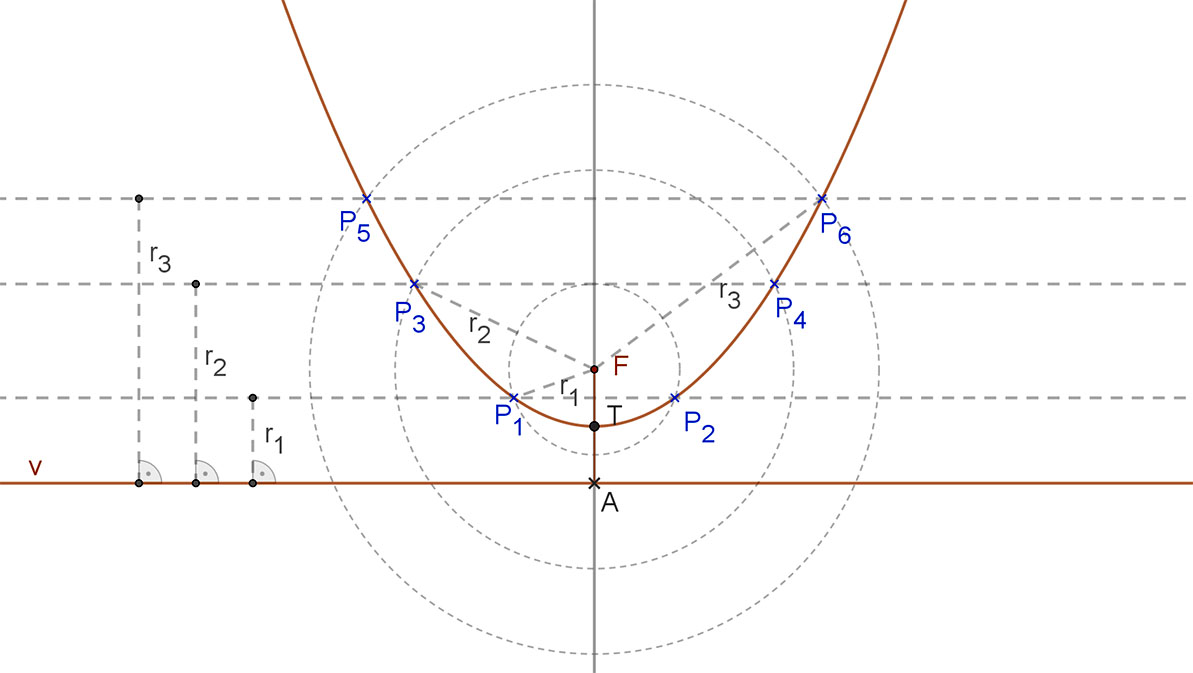A fenti módon tehát a parabola tetszőleges, de véges számú diszkrét pontja szerkeszthető. Az így megszerkesztett pontokra a parabola íve jó közelítéssel illeszthető.
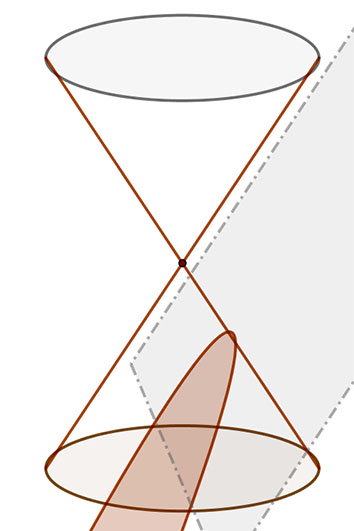A parabolát azonban mint kúpszeletet is definiálhatjuk.
Parabolát kapunk akkor is, ha egy forgáskúpot olyan síkkal metsszünk, amely nem megy át a kúp csúcspontján, és a metsző sík egy alkotóval párhuzamos.
A derékszögű koordináta rendszer alkalmaz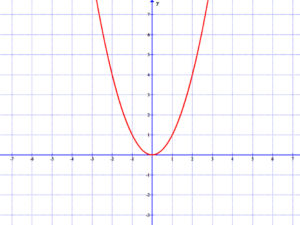
ása lehetővé tette a parabola analitikus tárgyalását.
A másodfokú függvény grafikonja is parabola.
A mellékelt ábrán szereplő függvény képlete: f(x)=x2. Ennek egyenlete: y=x2.
Comments are closed, but trackbacks and pingbacks are open.