Adott tulajdonságú pontok összességét mértani helynek mondjuk.
Az alábbiakban a következő mértani helyekről lesz szó:
- Két ponttól egyenlő távol lenni. (szakaszfelező merőleges)
- Két egyenestől egyenlő távol lenni. (szögfelező, illetve a középpárhuzamos)
- Adott ponttól adott távolságra lenni. (kör, illetve a gömb)
- Két adott pontól való állandó távolságösszeg. (az ellipszis)
- Két adott pontól való állandó távolságkülönbség. (a hiperbola)
- Adott ponttól és adott egyenestől egyenlő távol lenni. (parabola)
- Két adott ponttól való távolságok aránya állandó. (Apollóniosz-kör)
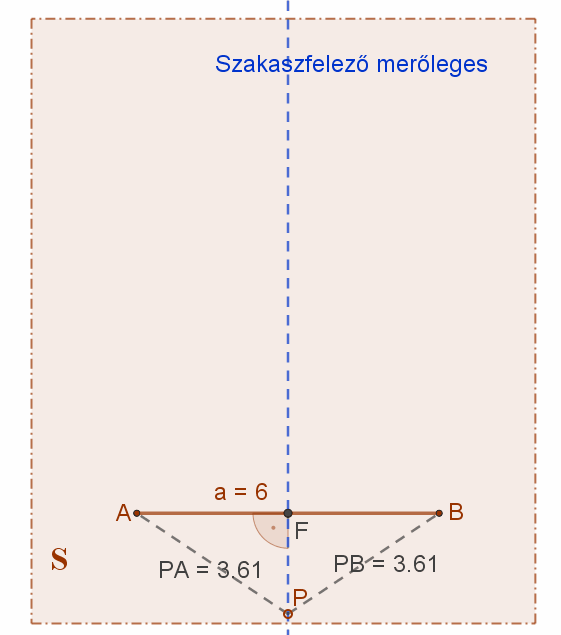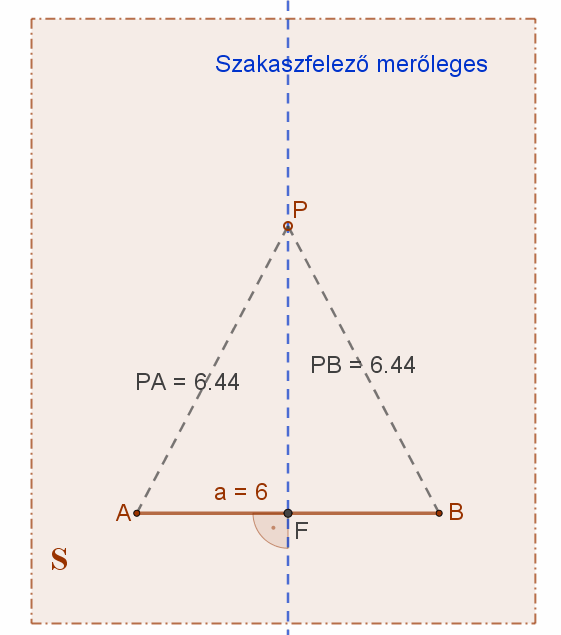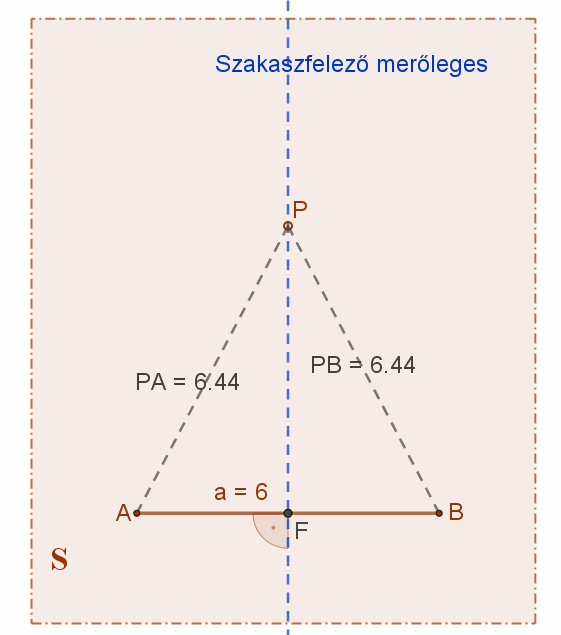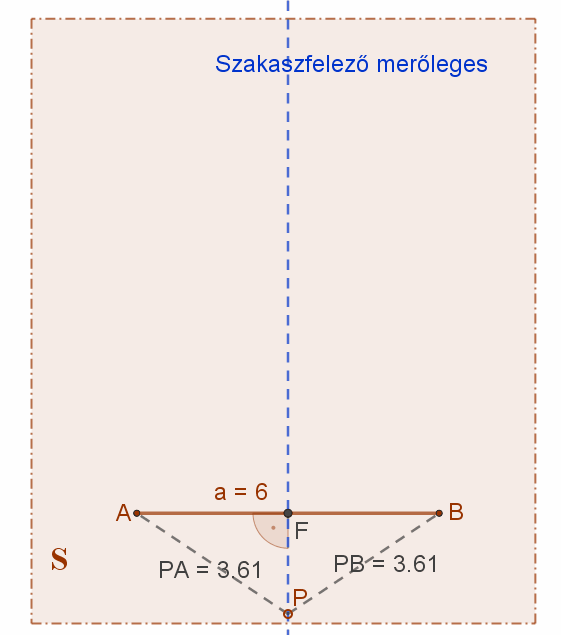
1. Két ponttól egyenlő távolságra lévő pontok halmaza a síkban: ez a szakaszfelező merőleges egyenes.
Két adott, de különböző (A és B) pontoktól egyenlő távolságra lévő pontok halmaza a síkban az adott pontok által meghatározott (AB) szakasznak az adott (S) síkra illeszkedő felező merőleges egyenese (f).
Két ponttól egyenlő távolságra lévő pontok halmaza a térben: ez a szakaszfelező merőleges sík.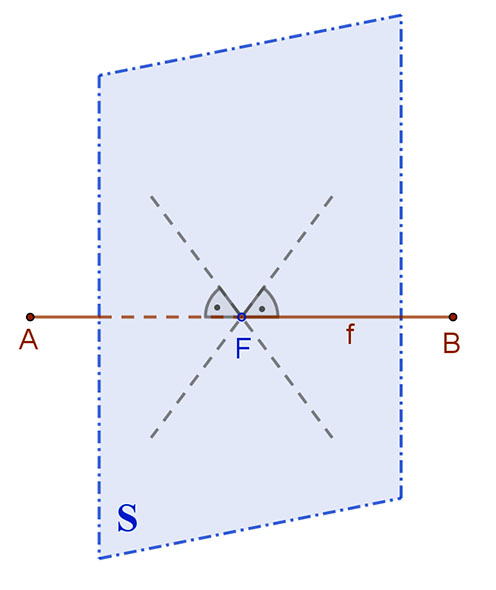
Két adott, de különböző (A és B) pontoktól egyenlő távolságra lévő pontok halmaza a térben az adott pontok által meghatározott (AB) szakasz felezőmerőleges síkja (S).
2. Két adott, de különböző egyenestől egyenlő távolságra lévő pontok halmaza a síkban.
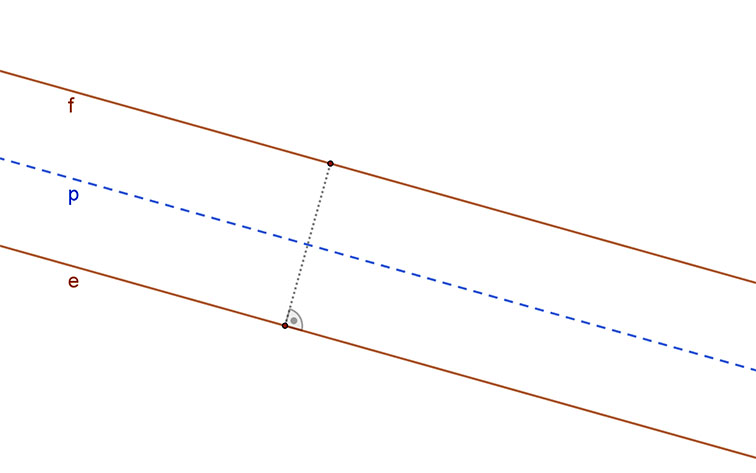1. Két adott (e és f) párhuzamos egyenestől egyenlő távolságra lévő pontok halmaza az adott egyenesek síkjában az a (p) egyenes, amelyik az adott egyenesekkel párhuzamos és a távolságukat felezi. (középpárhuzamos egyenes)
2. Két adott (a és b) metsző egyenestől egyenlő távolságra lévő pontok halmaza az adott egyenesek síkjában az egyenesek által bezárt szögek szögfelező egyenesei (f1, f2). A két szögfelező merőleges egymásra.
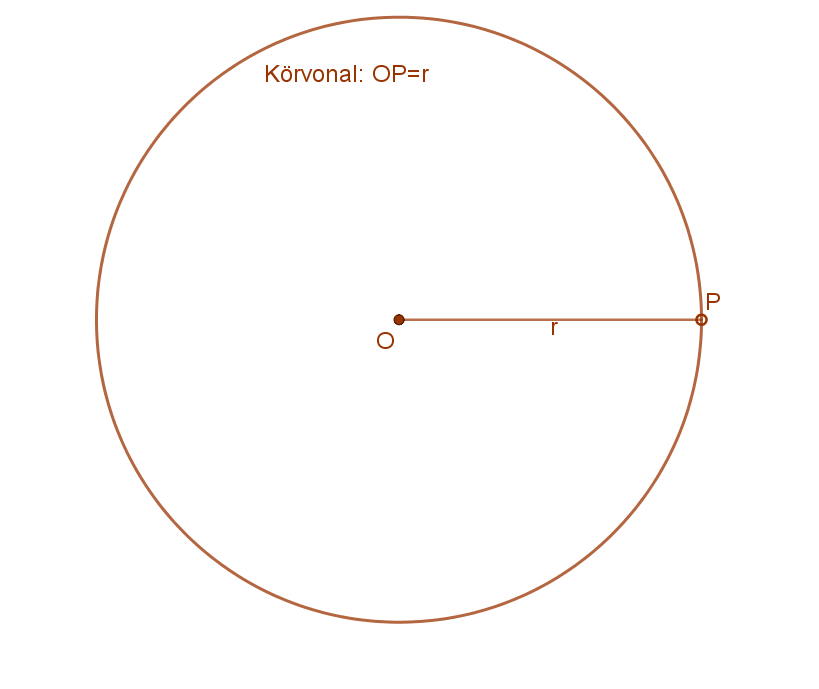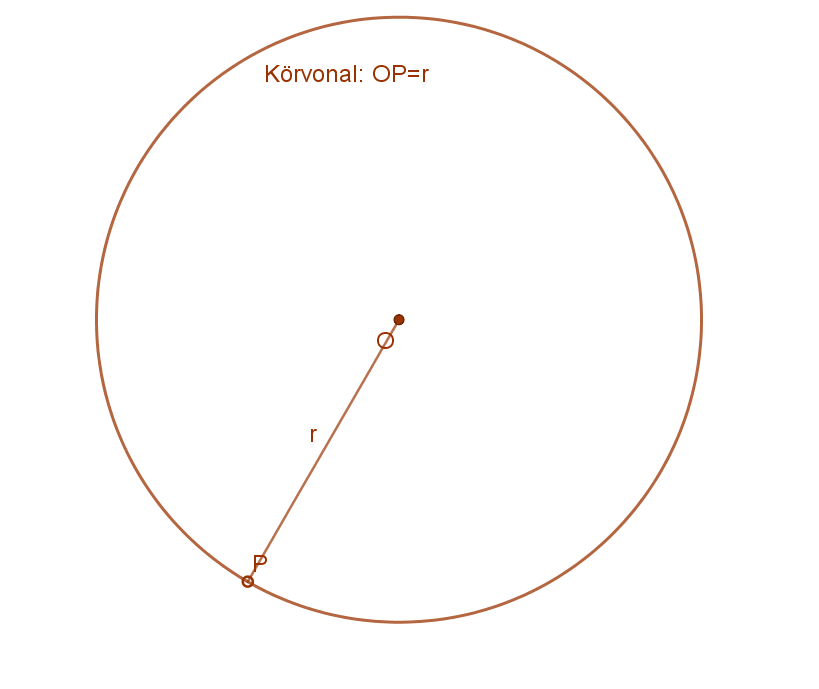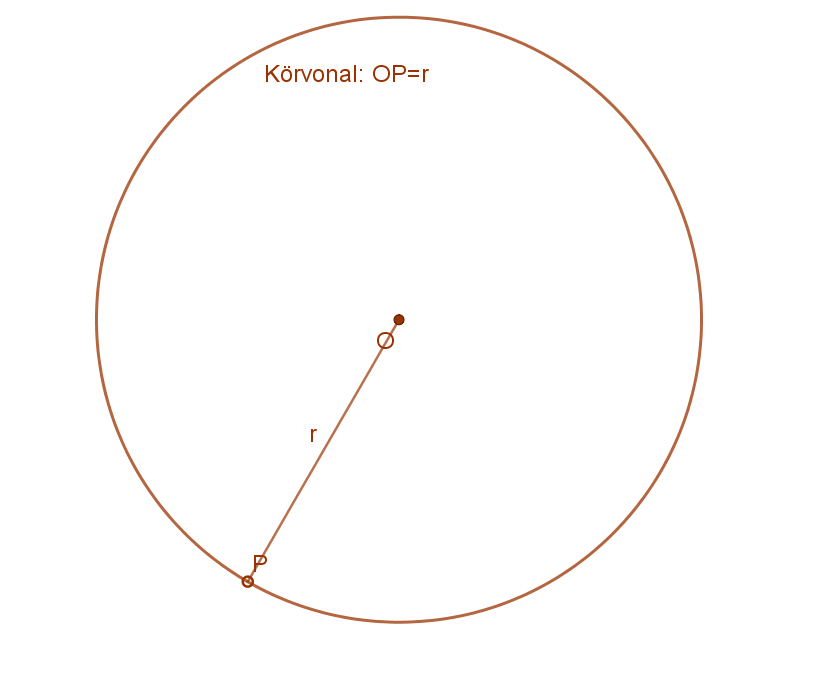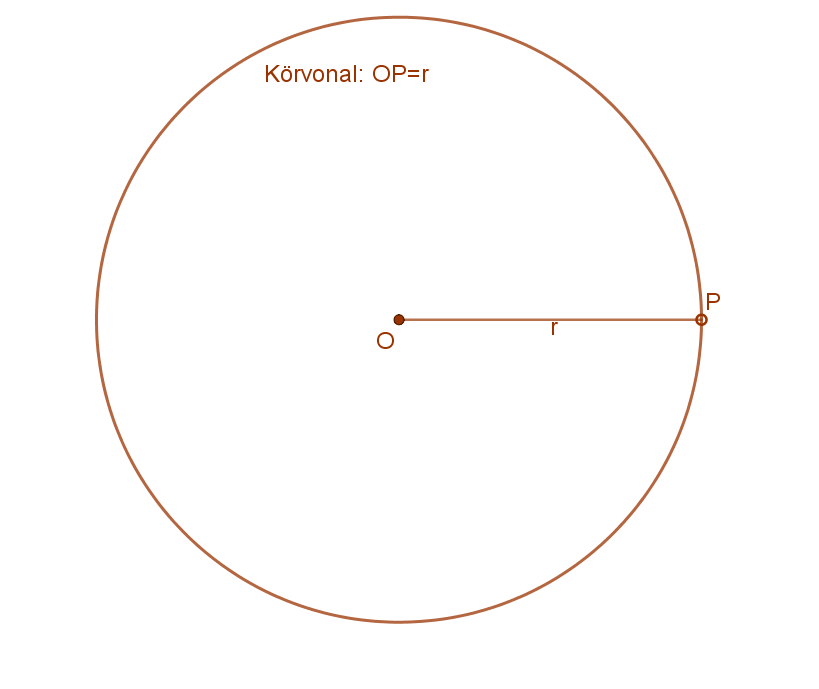
3. Adott ponttól adott távolságra lévő pontok halmaza a síkban: ez a körvonal.
Definíció:
A körvonal azoknak a pontoknak az összessége (mértani helye) a síkban, amelyek egy adott ponttól, a kör K középpontjától adott távolságra (r sugár) vannak.
Formulával: körvonal={P|d(P;O)=r}.
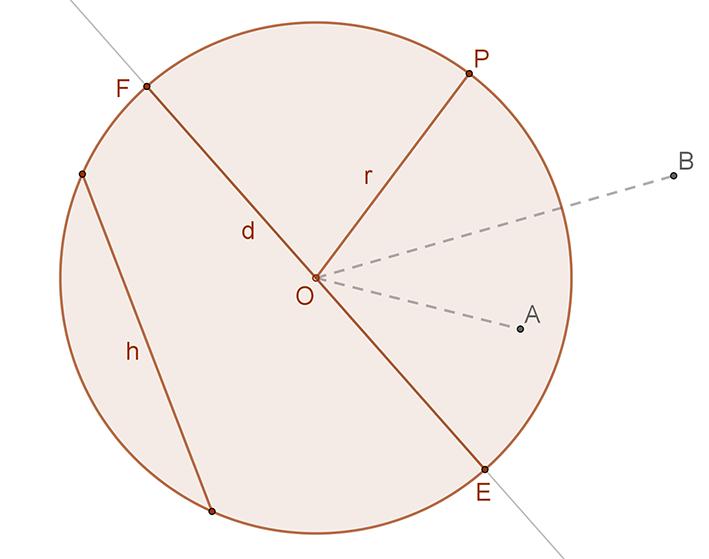A körvonal két pontját összekötő szakasz a kör húrja (h).
A kör középpontján áthaladó húr a kör átmérője (d), amely a sugár kétszerese. (d=2r).
A körvonalon belüli (A) pontok a középponttól a sugárnál kisebb távolságra vannak. d(A;O)<r.
A körvonalon kívüli (B) pontok a középponttól a sugárnál nagyobb távolságra vannak. d(B;O)>r.
Definíciók:
A (zárt) körlemez azoknak a pontoknak az összessége (mértani helye) a síkban, amelyek egy adott ponttól, a kör K középpontjától adott távolságnál (r sugár) nem nagyobb távolságra vannak.
Formulával: Zárt körlemez={P|d(P;O)≤ r}.
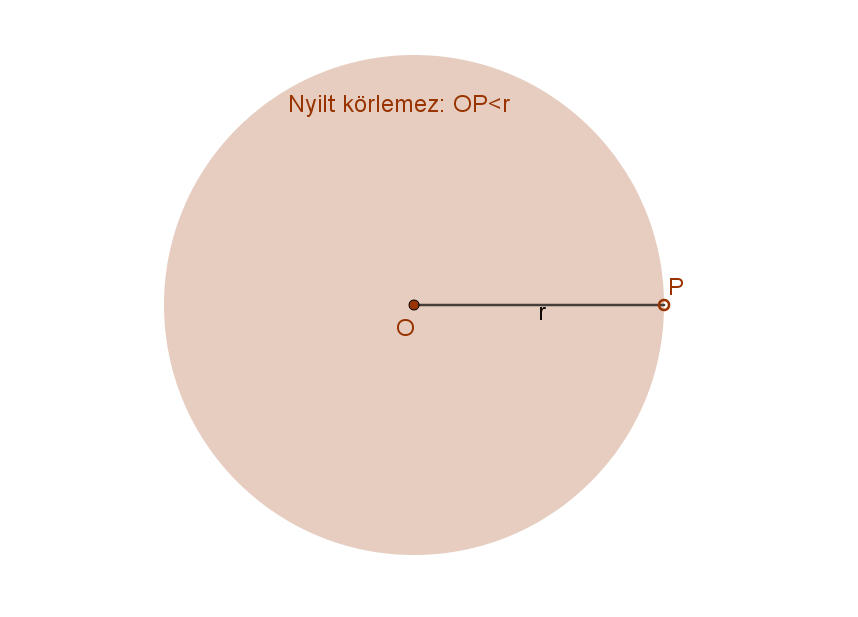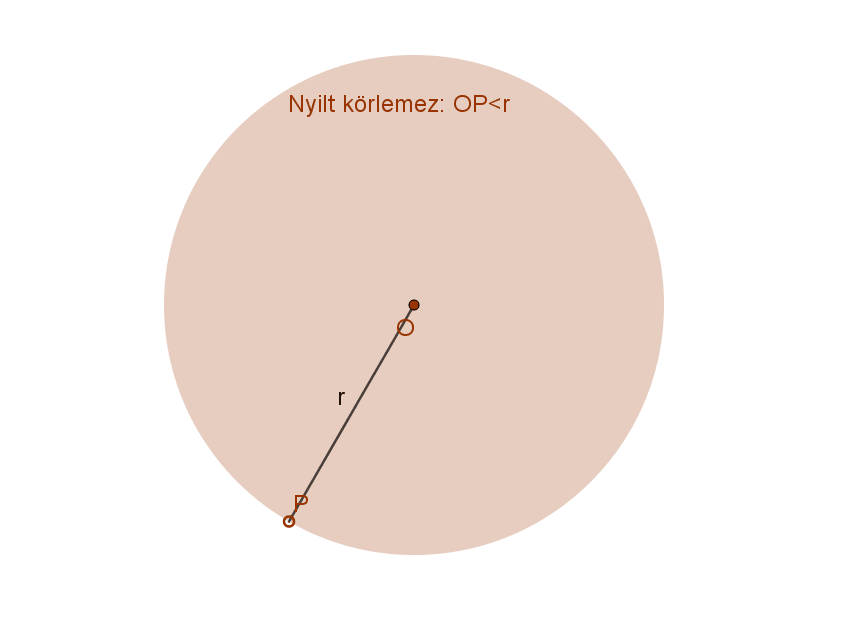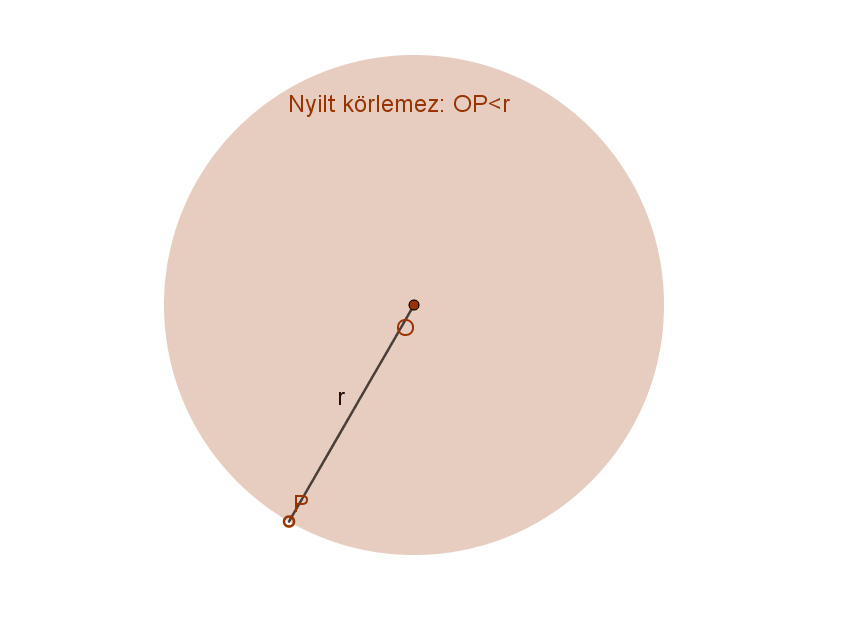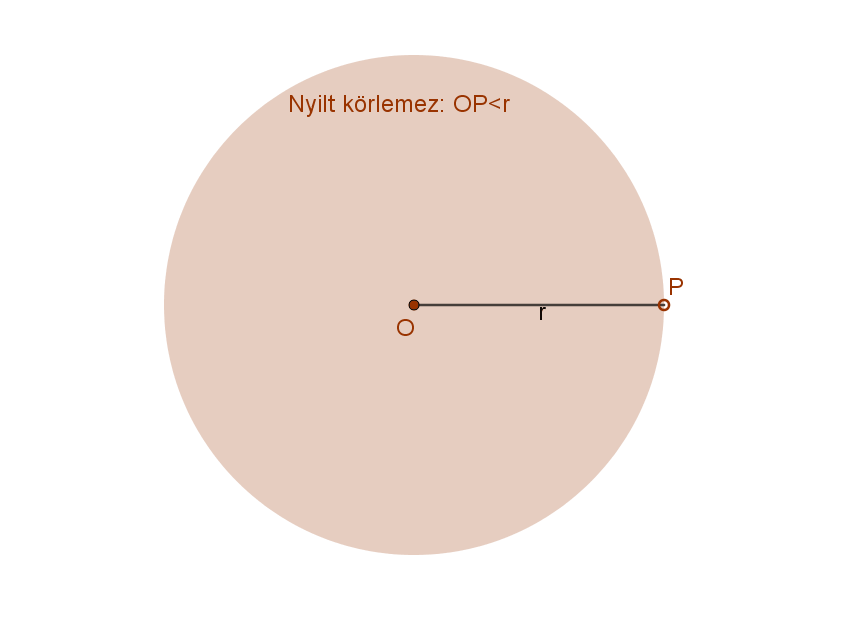
Nyílt körlemez azoknak a pontoknak az összessége (mértani helye) a síkban, amelyek egy adott ponttól, a kör K középpontjától adott távolságnál (r sugár) kisebb távolságra vannak.
Megjegyzés: A zárt és a nyílt körlemezek kerülete és a területeik is egyenlő. Zárt körvonalról leválasztva a körvonal pontjait, sem a kerület, sem a terület nem változik.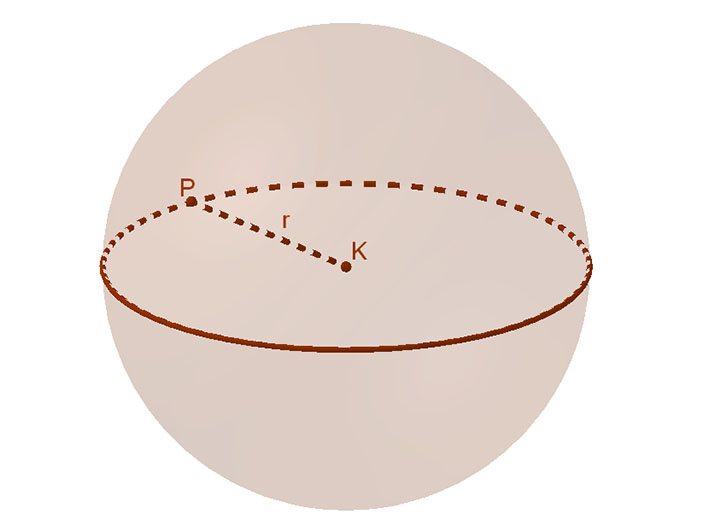
Adott ponttól adott távolságra lévő pontok halmaza a térben: ez a gömbfelület.
Definíció:
A gömbfelület azoknak a pontoknak az összessége a térben, amelyek egy adott ponttól, a gömb K középpontjától adott távolságra (r sugár) vannak.
Formulával: gömbfelület={P|d(P;K)=r}.
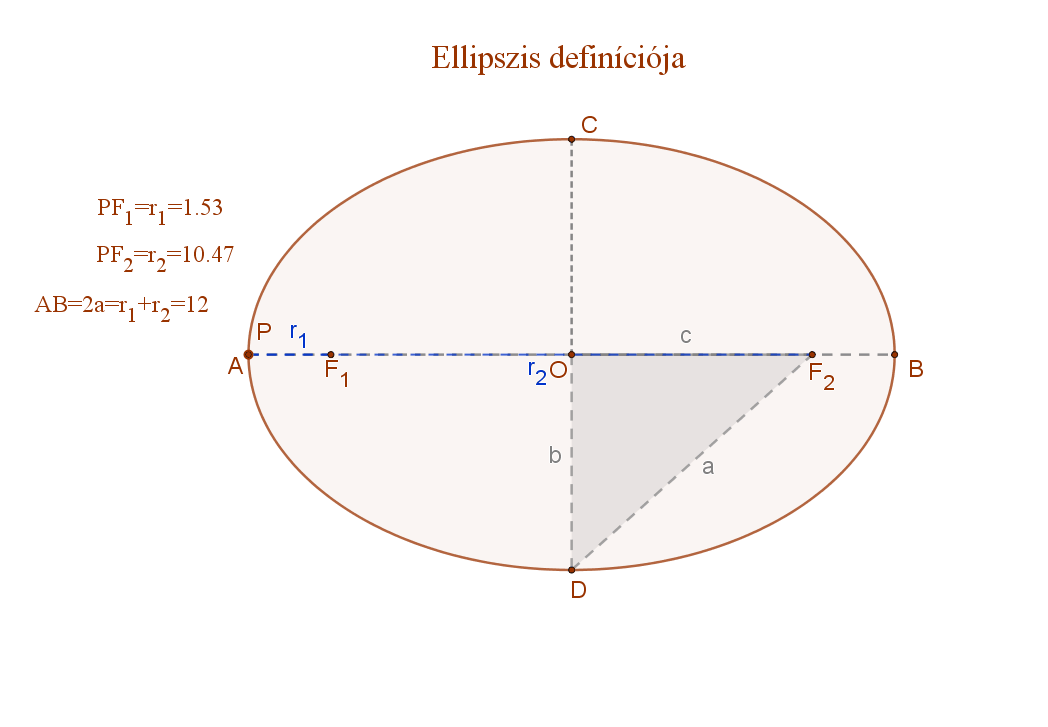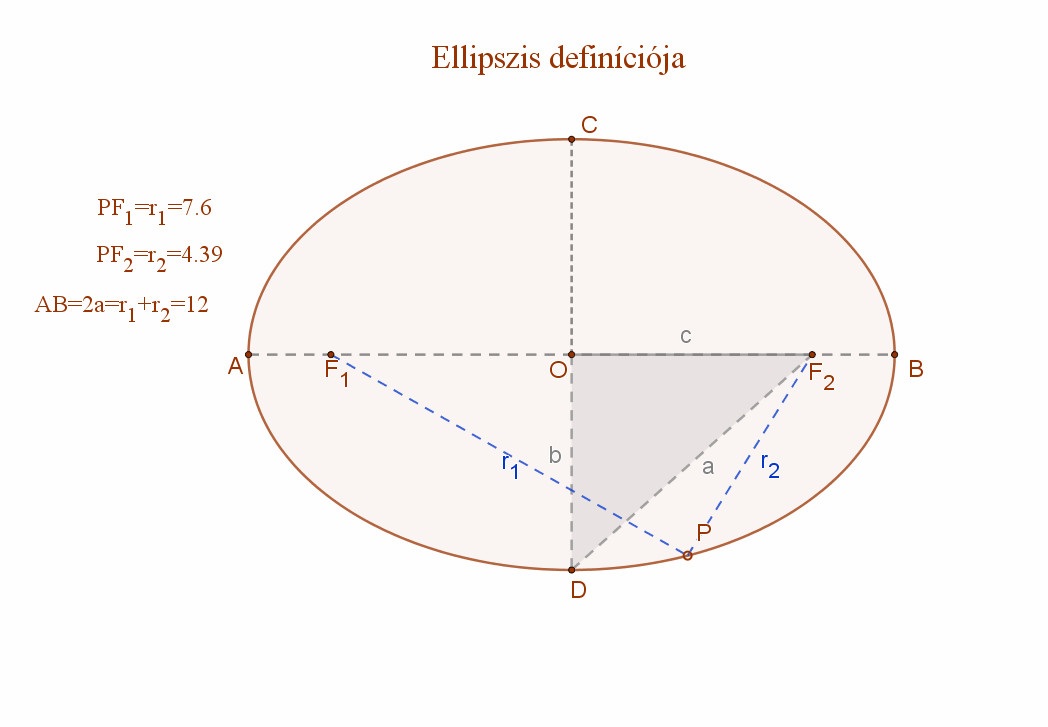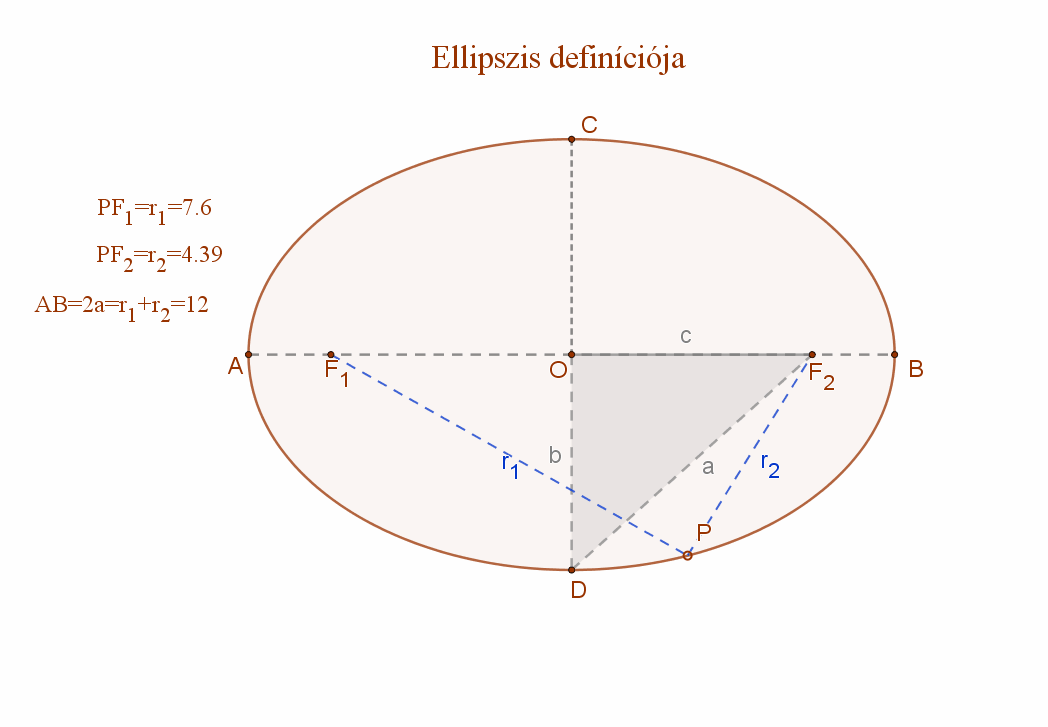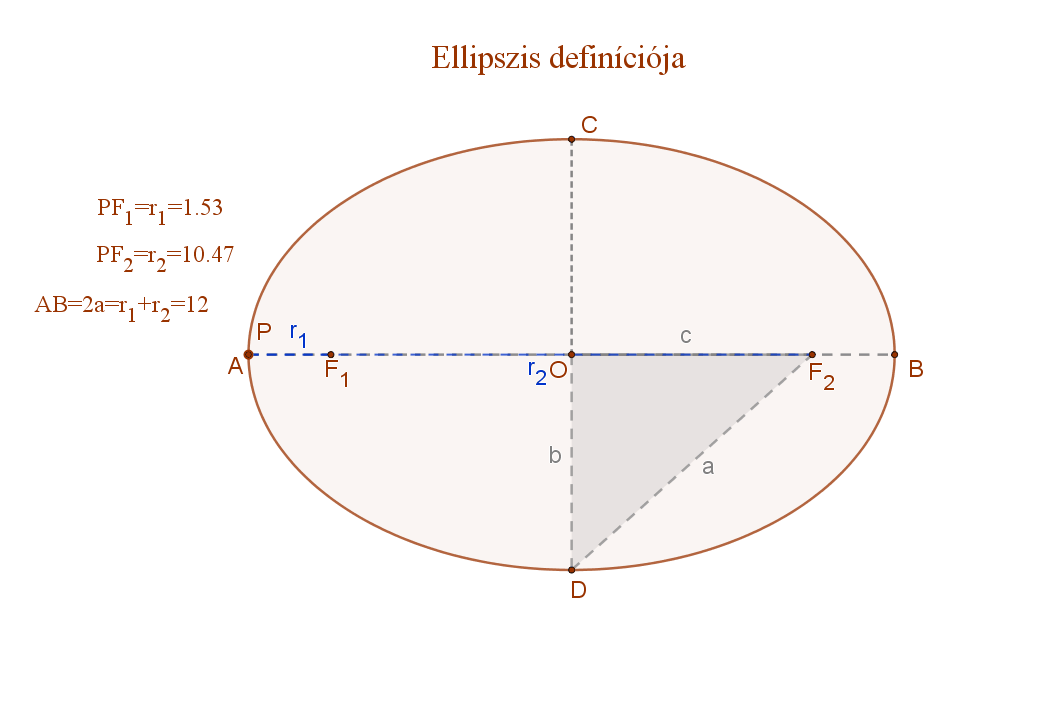
4. Két adott ponttól való távolságuk összege állandó: ez az ellipszis.
Definíció:
Az ellipszis azoknak a P pontoknak az összessége (mértani helye) a síkban, amelyek a sík két adott pontjától, az F1 és F2 fókuszpontoktól való távolságaik (r1, és r2 vezérsugarak) összege állandó (2a).
Ez a távolság nagyobb kell legyen, mint a két fókuszpont távolsága.
Formulával: ellipszis={P|d(P,F1)+d(P,F2)=r1+r2=állandó=2a>d(F1;F2).
Megjegyzés: Ha a két fókusz egybeesik, akkor kört kapunk.
A mellékelt ábra jelölései szerint:
F1 és F2: az ellipszis fókuszpontjai, F1F2=2c
AB=az ellipszis nagytengelye=2a.
P az ellipszis egy tetszőleges pontja. PF1+PF2=2a.
PF1 és PF2 szakaszok: r1 és r2 vezérsugarak.
CD=az ellipszis kistengelye (2b).
Az ellipszis vonala euklideszi értelemben nem szerkeszthető, de véges számú pontja igen.
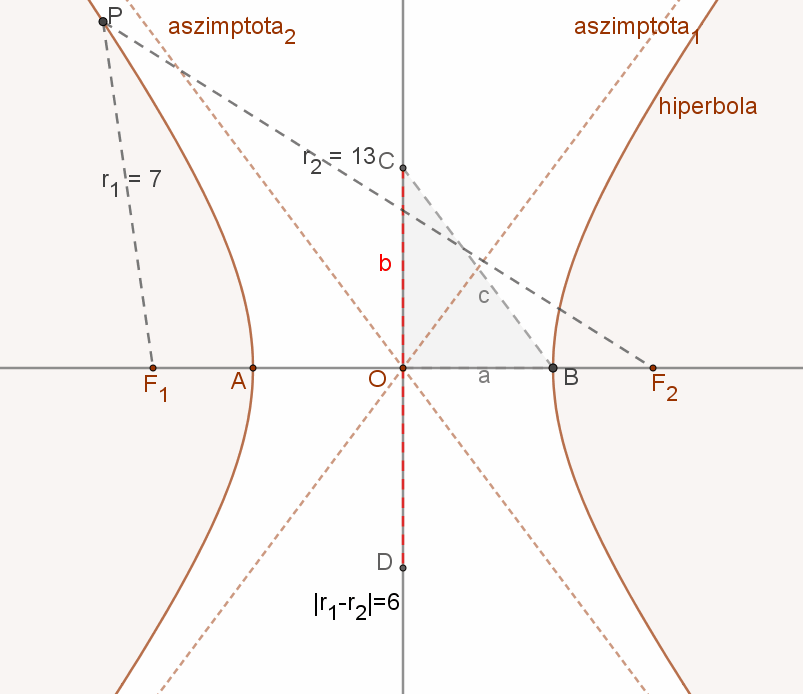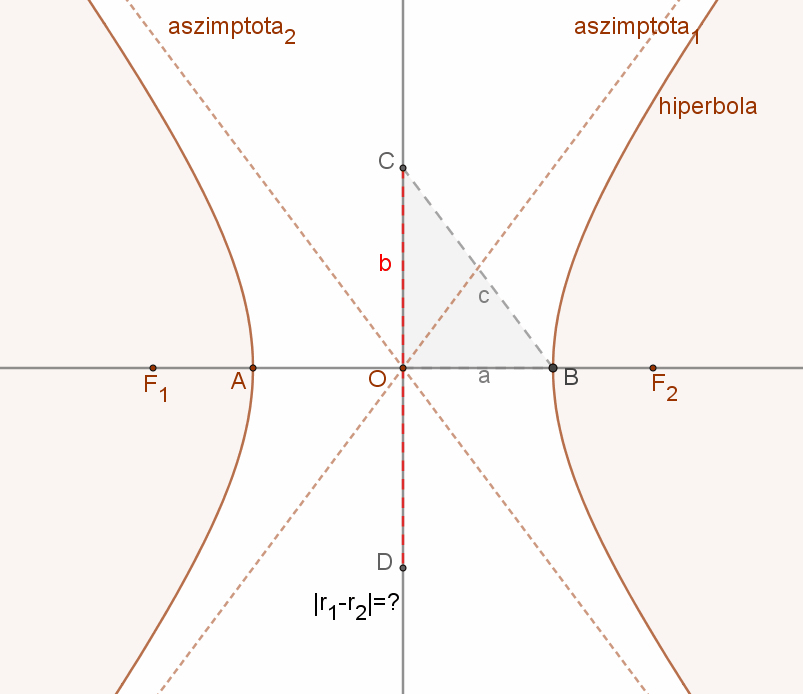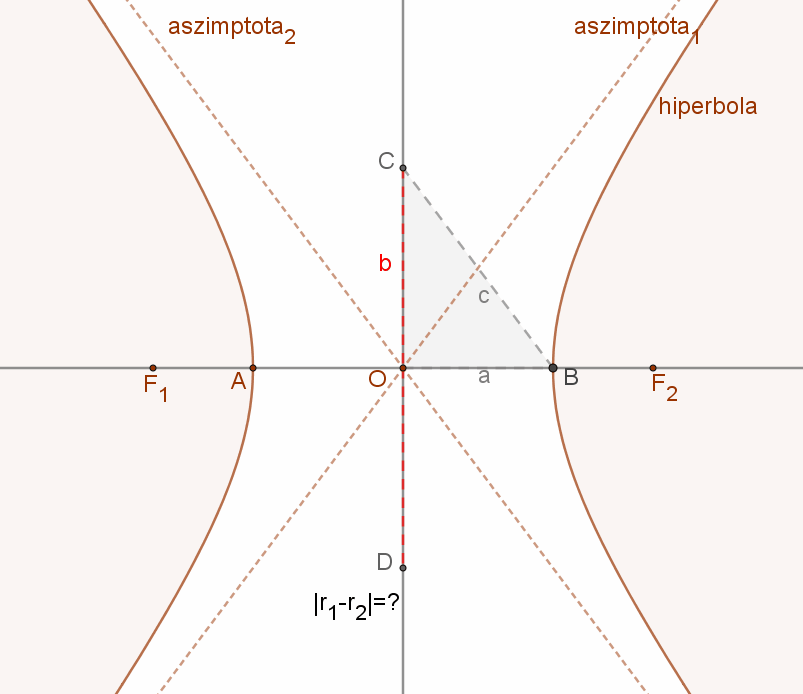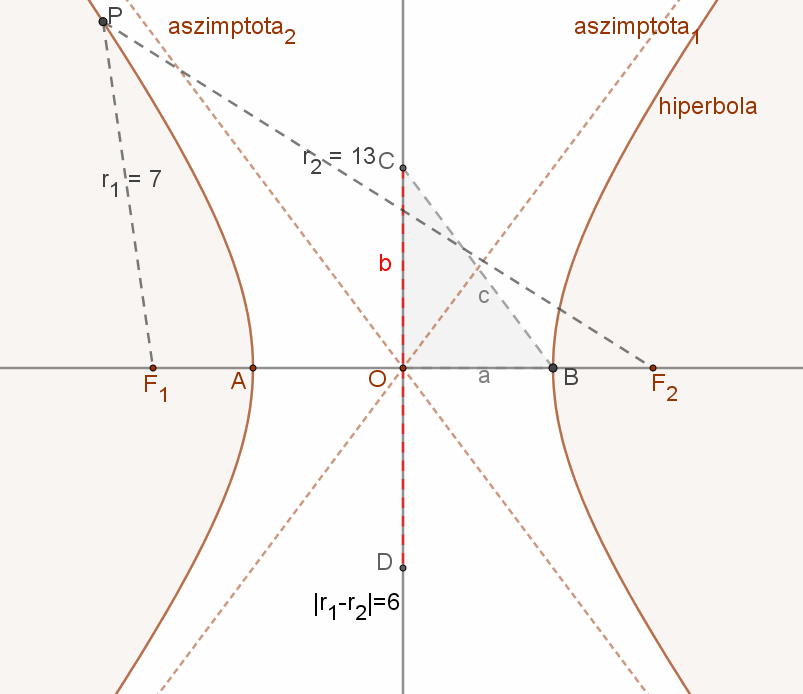
5. Két adott ponttól valós távolságuk különbségének abszolút értéke állandó: ez a hiperbola.
Definíció:
A hiperbola azoknak a P pontoknak az összessége (mértani helye) a síkban, amelyek a sík két adott pontjától, az F1 és F2 fókuszpontoktól való távolságaik (r1, és r2 vezérsugarak) különbségének abszolút értéke állandó (2a).
Ez a távolság kisebb kell legyen, mint a két fókuszpont távolsága.
Formulával: hiperbola={P|(|d(P,F1)-d(P,F2)|)=|r1–r2|=állandó=2a<d(F1;F2).
A mellékelt ábra jelölései szerint:
F1 és F2: a hiperbola fókuszpontjai. F1F2=2c.
AB=a hiperbola valós tengelye=2a.
P a hiperbola egy tetszőleges pontja.
|PF1-PF2|=2a.
PF1 és PF2 szakaszok: r1 és r2 vezérsugarak.
CD=a hiperbola képzetes tengelye=2b.
A hiperbola vonala euklideszi értelemben nem szerkeszthető, de véges számú pontja igen.
6. Adott egyenestől és adott ponttól egyenlő távolságra lévő pontok halmaza: ez a parabola.
Definíció:
A parabola azoknak a pontoknak az összessége (mértani helye) a síkban, amelyek a sík egy adott egyenesétől (vezéregyenes) és a sík egy adott (a vezéregyenesre nem illeszkedő) pontjától (fókusz) egyenlő távolságra vannak.
Formulával: parabola={P|d(P,v)=d(P,F).
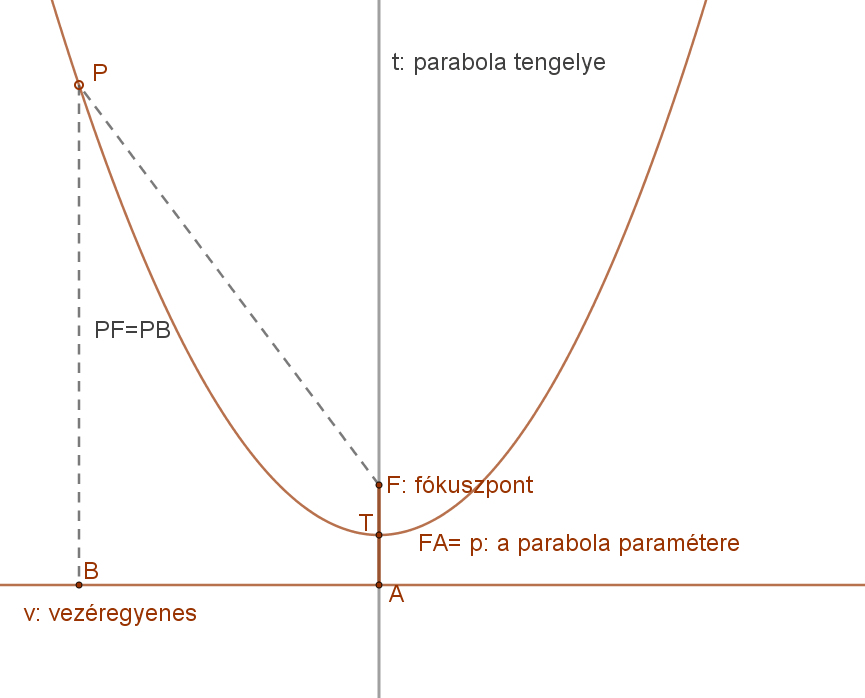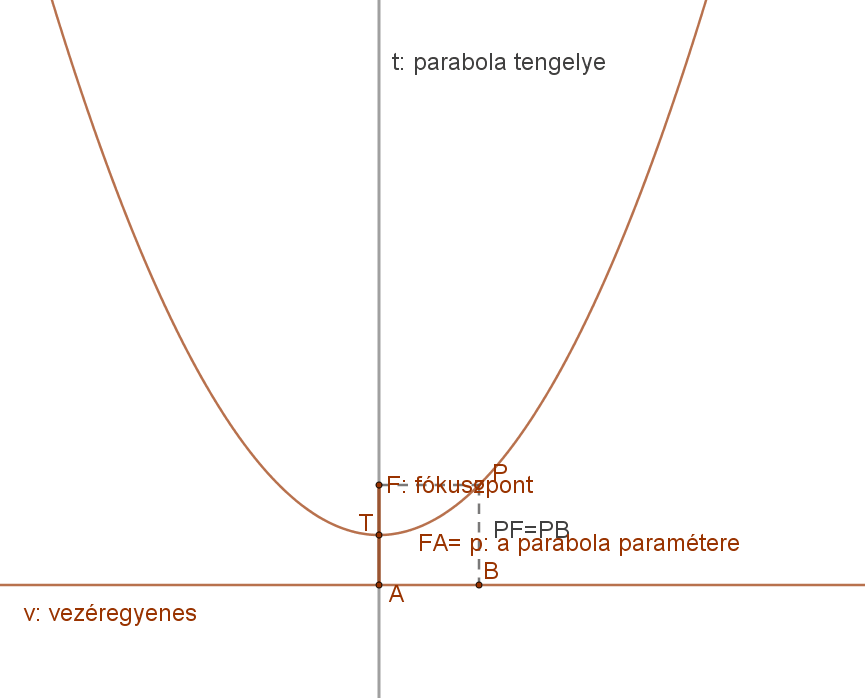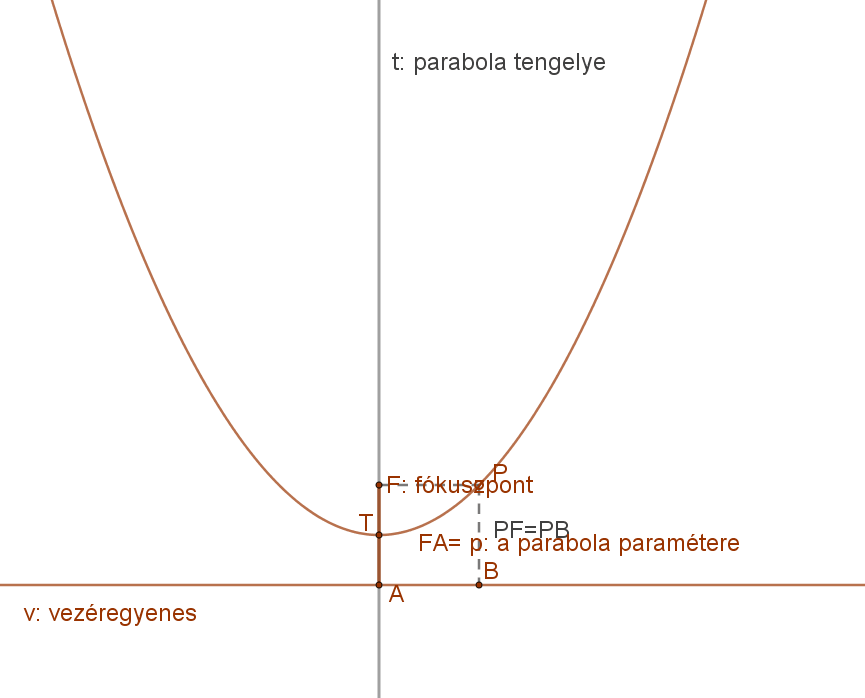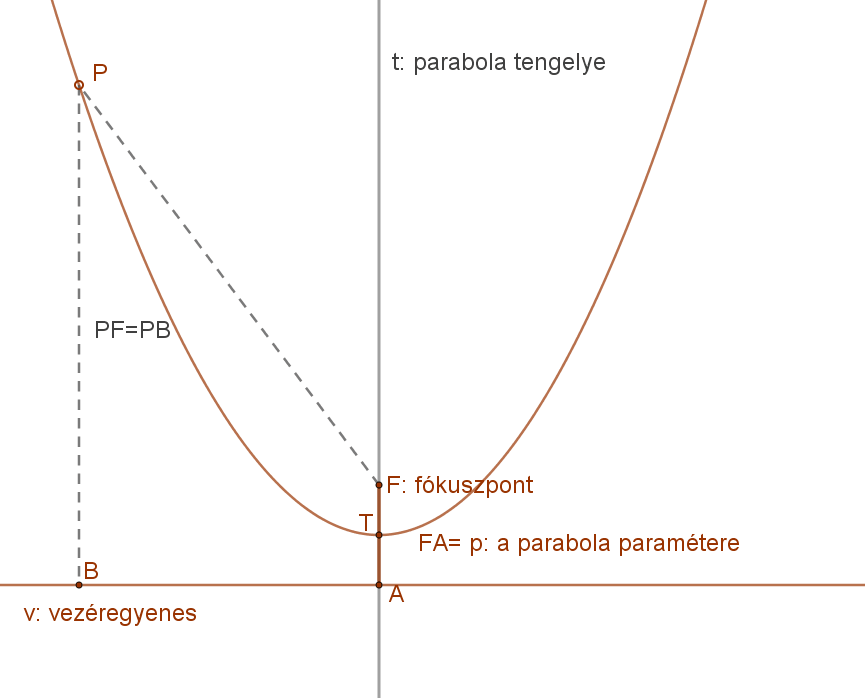A mellékelt ábra jelölései szerint:
v: vezéregyenes,
F: fókuszpont.
p: fókuszpont és vezéregyenes távolsága, a parabola paramétere.
P: a parabola egy tetszőleges pontja.
t: parabola tengelye,
T: parabola tengelypontja.
A parabola euklideszi értelemben nem szerkeszthető, de véges számú pontja igen.
7. Két adott ponttól való távolságuk aránya állandó: ez az Apollóniosz kör.
Definíció:
Apollóniosz kör azon pontok halmaza síkban, amely pontoknak két adott ponttól való távolságainak aránya állandó.
Formulával: Apollóniosz kör={P|AP:BP=m:n}.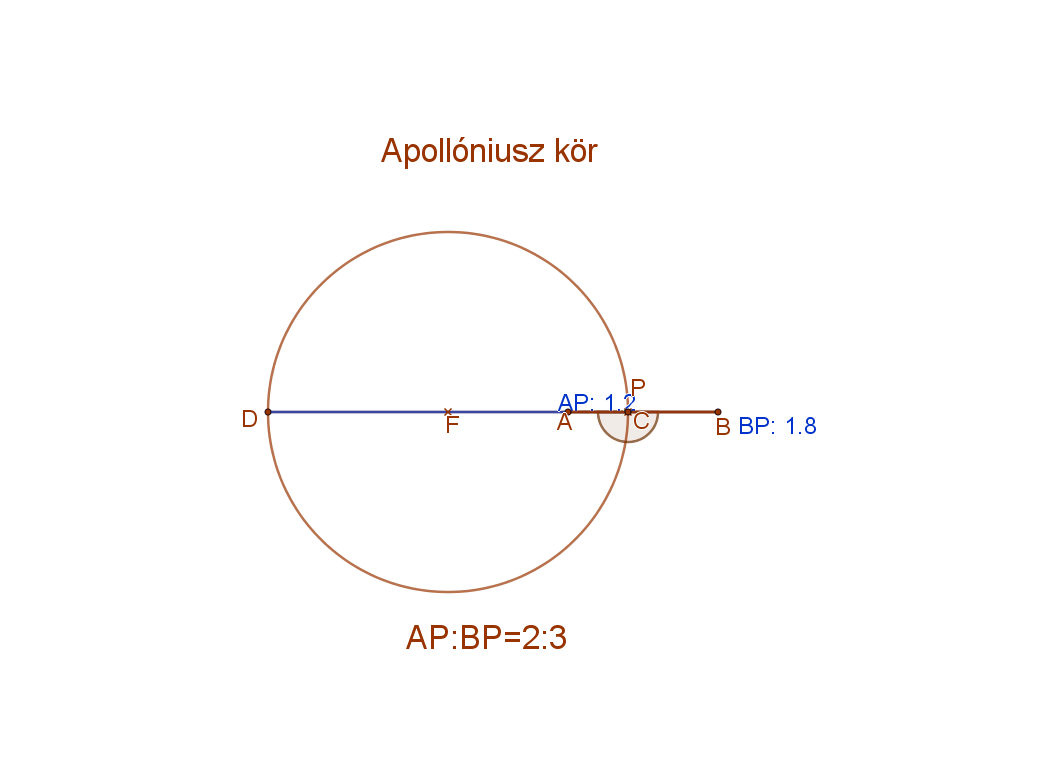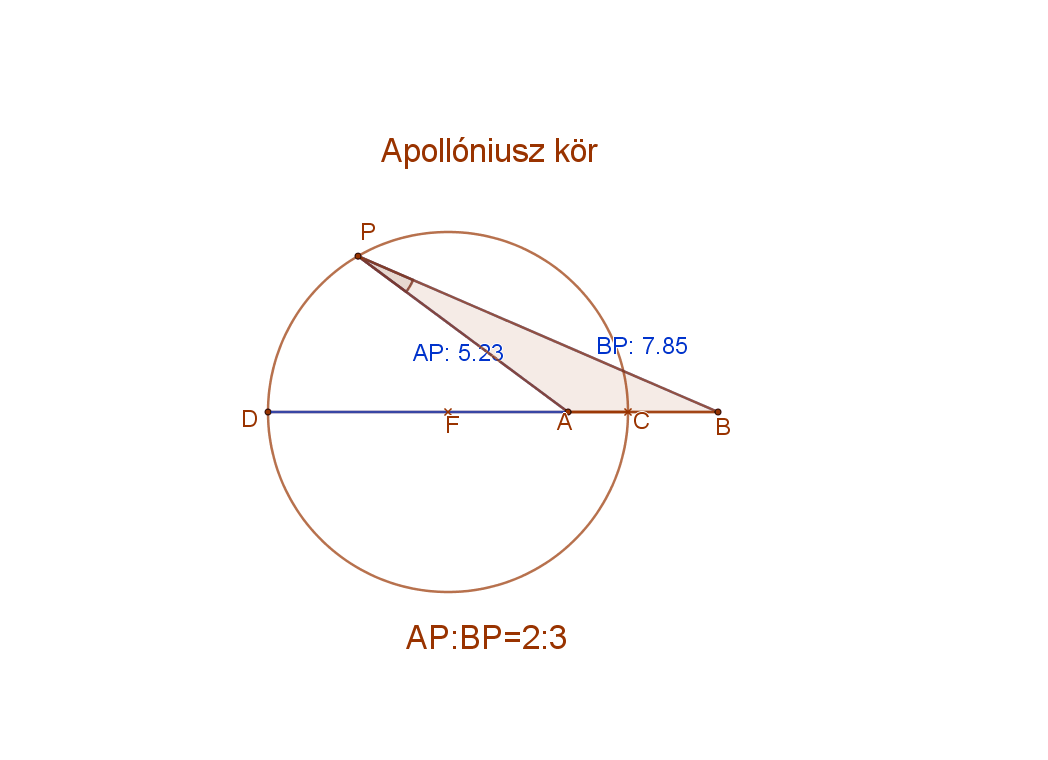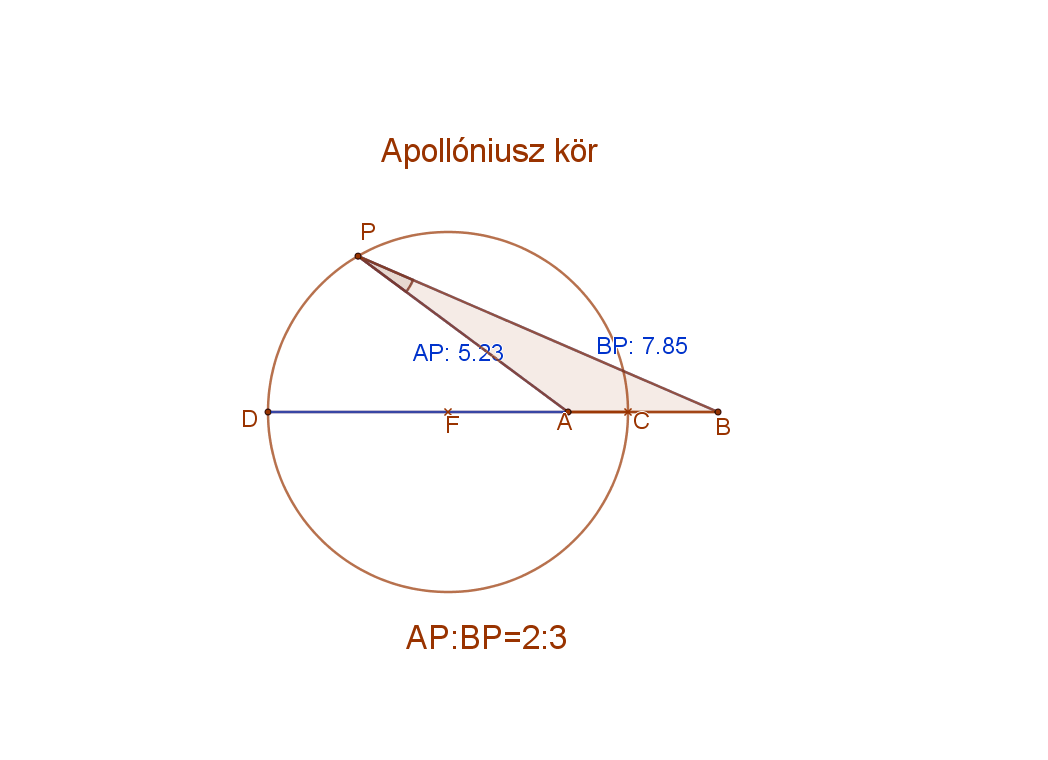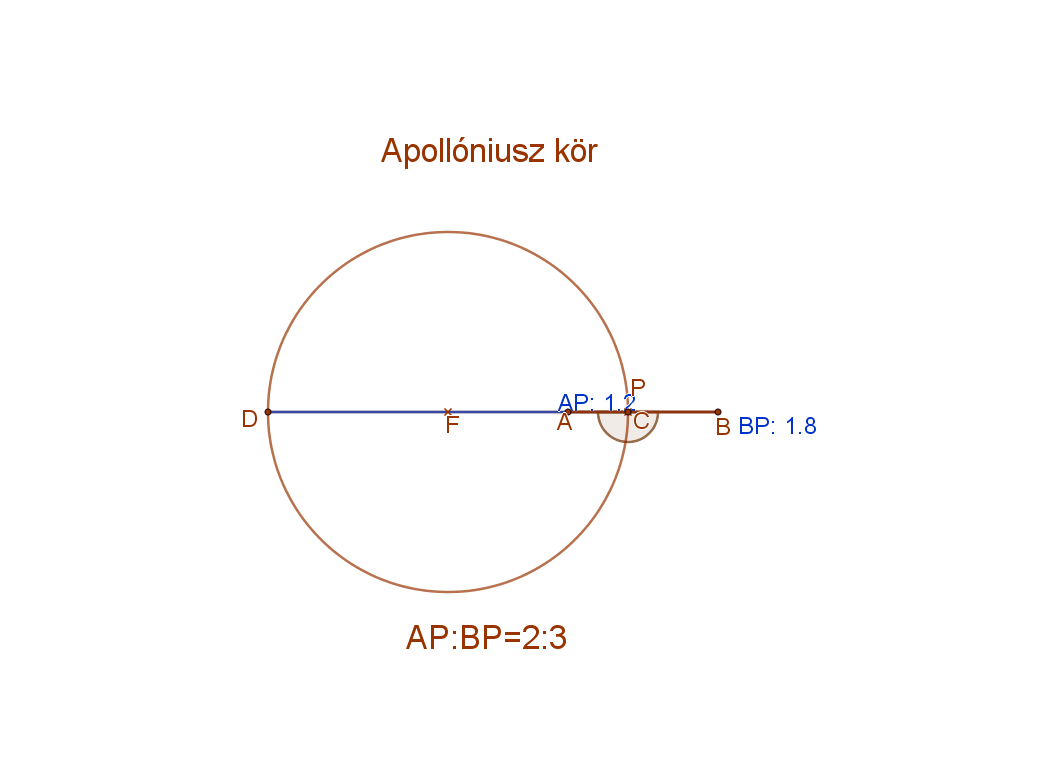
Comments are closed, but trackbacks and pingbacks are open.