Ellipszis, mint adott tulajdonságú pontok halmaza

Definíció: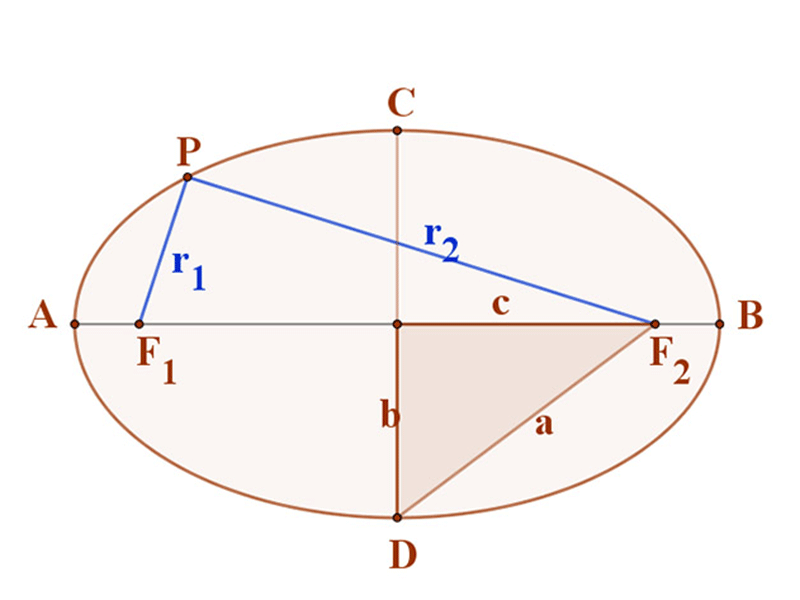

Az ellipszis azoknak a P pontoknak az összessége (mértani helye) a síkban, amelyek a sík két adott pontjától, az F₁ és F₂ fókuszpontoktól való távolságaik (r₁, és r₂ vezérsugarak) összege állandó (2a).
Ez a távolság nagyobb kell legyen, mint a két fókuszpont távolsága (2c).

Formulával: ellipszis={P|d(P,F₁)+d(P,F₂)=r₁+r₂=állandó=2a>d(F₁;F₂)=2c.

Megjegyzés: Ha a két fókusz egybeesik, akkor kört kapunk.

A két fókuszpont egyenese az ellipszis szimmetriatengelye. Ennek a szimmetriatengelynek az ellipszissel két közös pontja van. Ennek a két metszéspontnak a távolsága (2a) az ellipszis nagytengelye. Ennek hossza egyenlő az ellipszis bármely pontjának a fókuszoktól való távolságok (r₁ és r₂ vezérsugarak) összegével. Ez a távolság az adott fókuszpontok mellett jellemző az ellipszisre.

A nagytengely felezőmerőlegese az ellipszis másik szimmetriatengelye. Ez is két pontban metszi az ellipszist. Ennek a két pontnak a távolságát (2b) az ellipszis kistengelyének nevezzük.

A két tengely metszéspontja (O) az ellipszis szimmetria középpontja.

A mellékelt animációs ábra jelölései szerint:

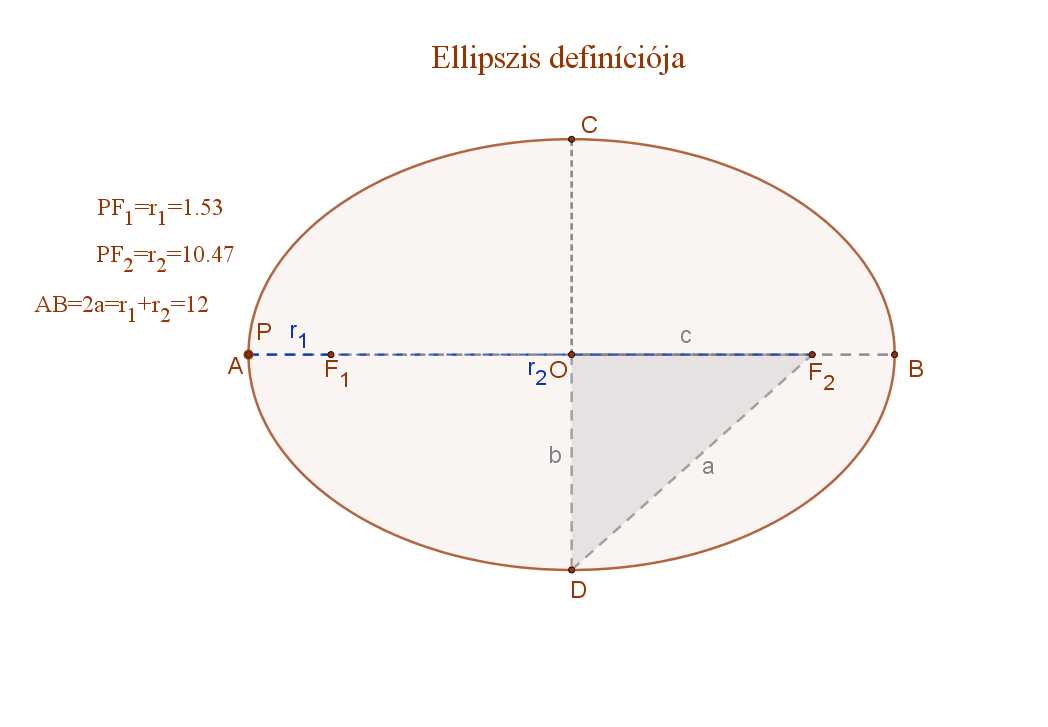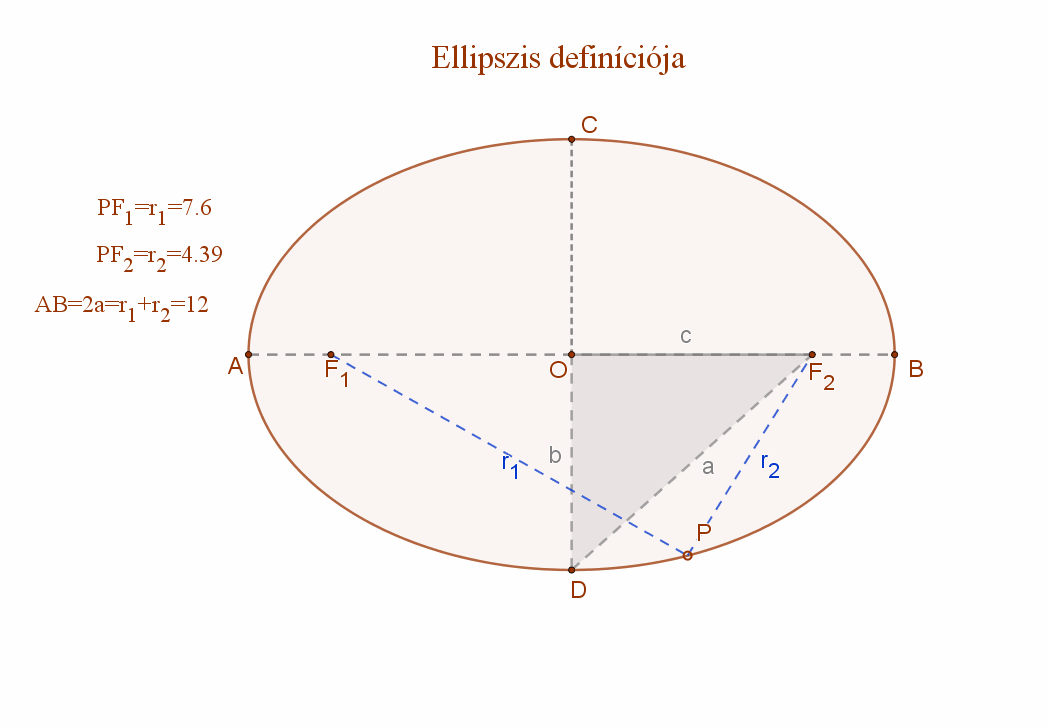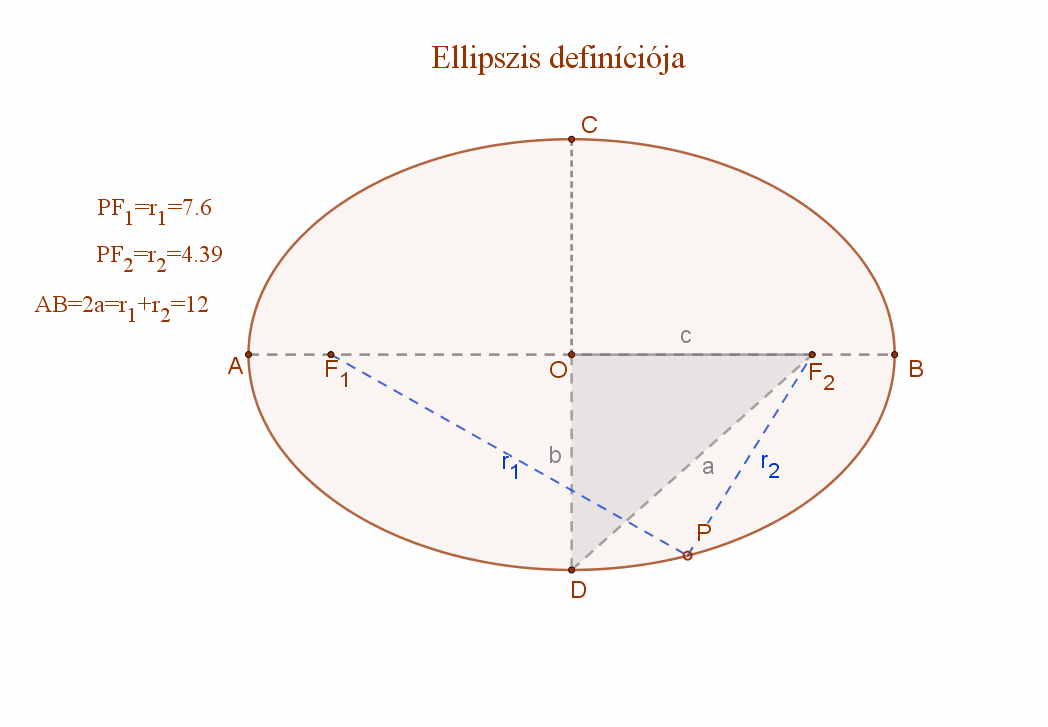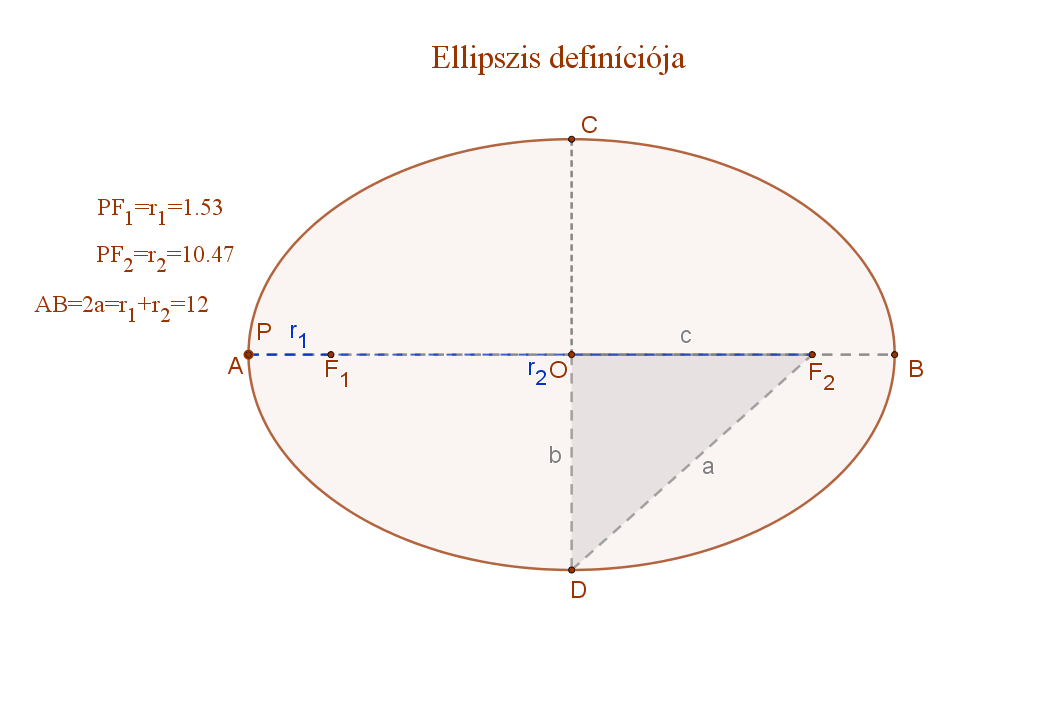
F₁ és F₂: az ellipszis fókuszpontjai.
A két fókuszpont távolsága: F₁F₂=2c.
AB=az ellipszis nagytengelye=2a.
P az ellipszis egy tetszőleges pontja.
PF₁ és PF₂ szakaszok: r₁ és r₂ vezérsugarak.
Definíció szerint: PF₁+PF₂=2a.
CD=az ellipszis kistengelye (2b).

Az ellipszis fókuszpontjai távolságának a fele (c), a nagytengely fele (a) és és kistengely fele (b) között az ODF₂ derékszögű háromszög alapján a következő összefüggés írható fel: a²=b²+c². (Pitagorasz tétele)

Az ellipszist tehát egyértelműen meghatározza:

1. A fókuszpontok távolsága. F₁F₂=2c.
2. Az ellipszisre jellemző állandó távolság összeg (a vezérsugarak összege), a nagytengely hossza: AB=2a.

Megjegyzés: Az  a²=b²+c² képlet segítségével bármelyik kettőből a harmadik számolható.

Ellipszis érintői

Definíció:

Egy ellipszis érintője olyan egyenes a síkon, amelynek egy adott ellipszissel egy és csak egy közös pontja van és minden más pontja külső pont.

Megjegyzés: Az ellipszis esetében elegendő lenne a körnél megismert definíció: Egy ellipszis érintője olyan egyenes a síkon, amelynek egy adott ellipszissel egy és csak egy közös pontja van.

Ellipszis és az érintők kölcsönös helyzete:

Az ellipszis pontjaiba húzott érintők a vezérsugarak által közrefogott szög külső szögének szögfelezője.
Az ellipszis tengelypontjaiban húzott érintők merőlegesek az adott tengelyre.

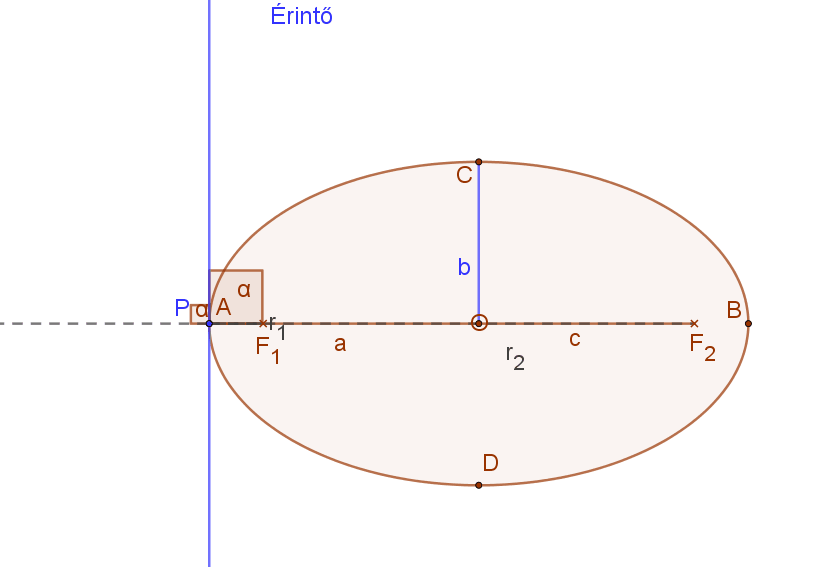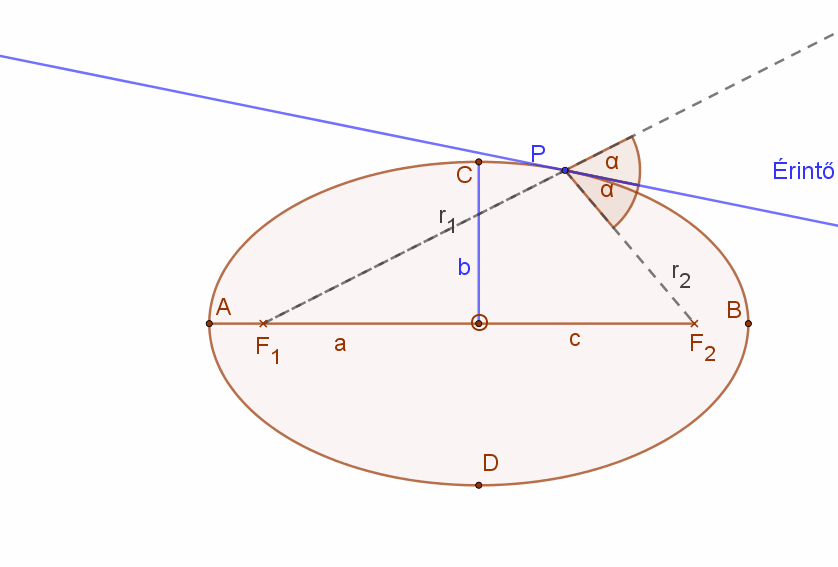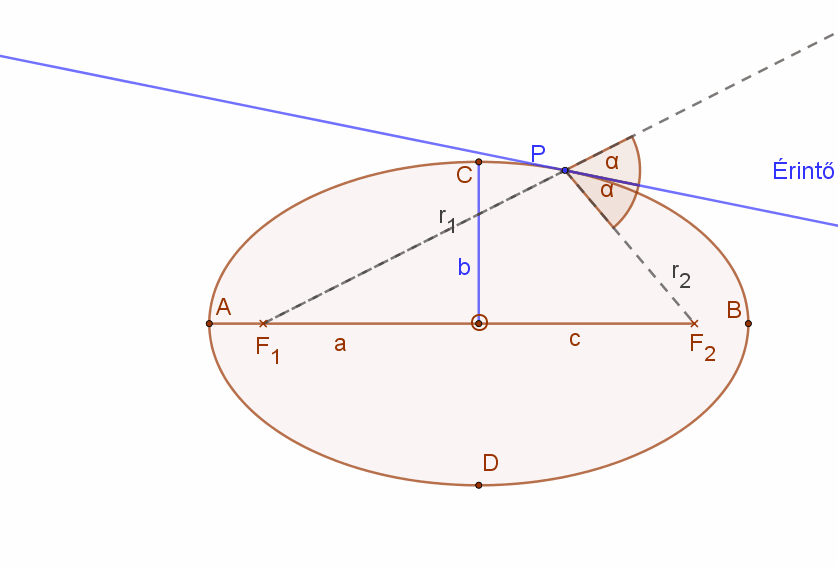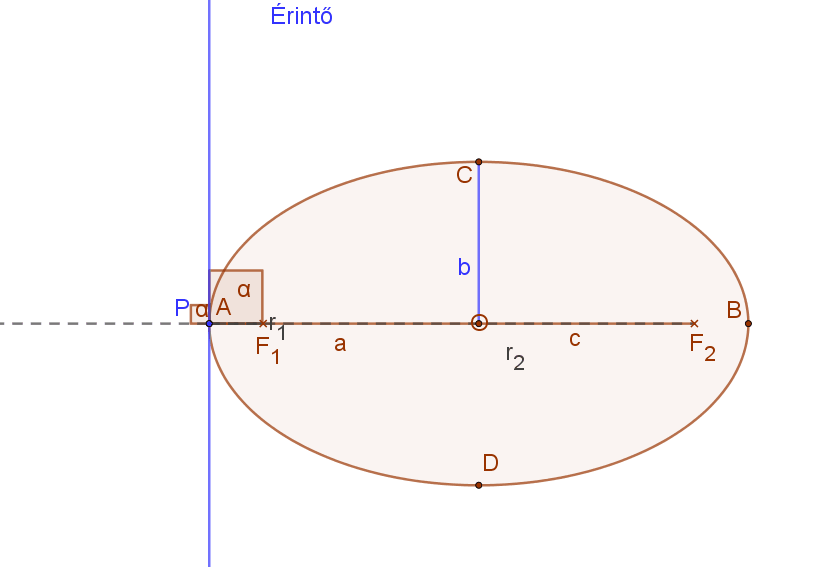
Ellipszishez külső pontból húzott érintők

A körhöz és a parabolához hasonlóan az ellipszishez külső pontból két érintő húzható.

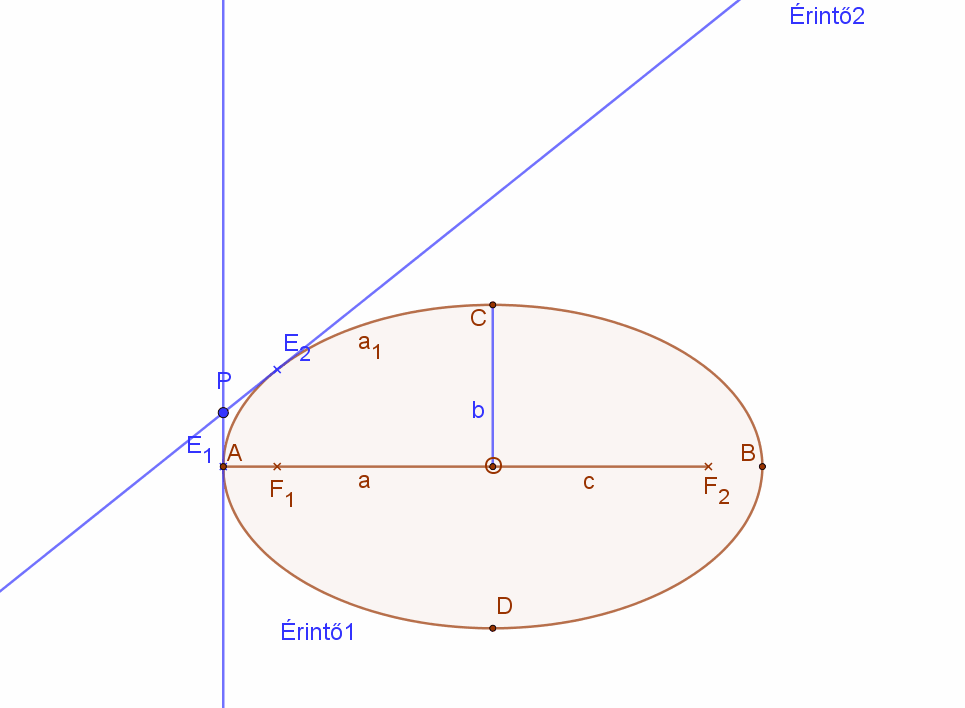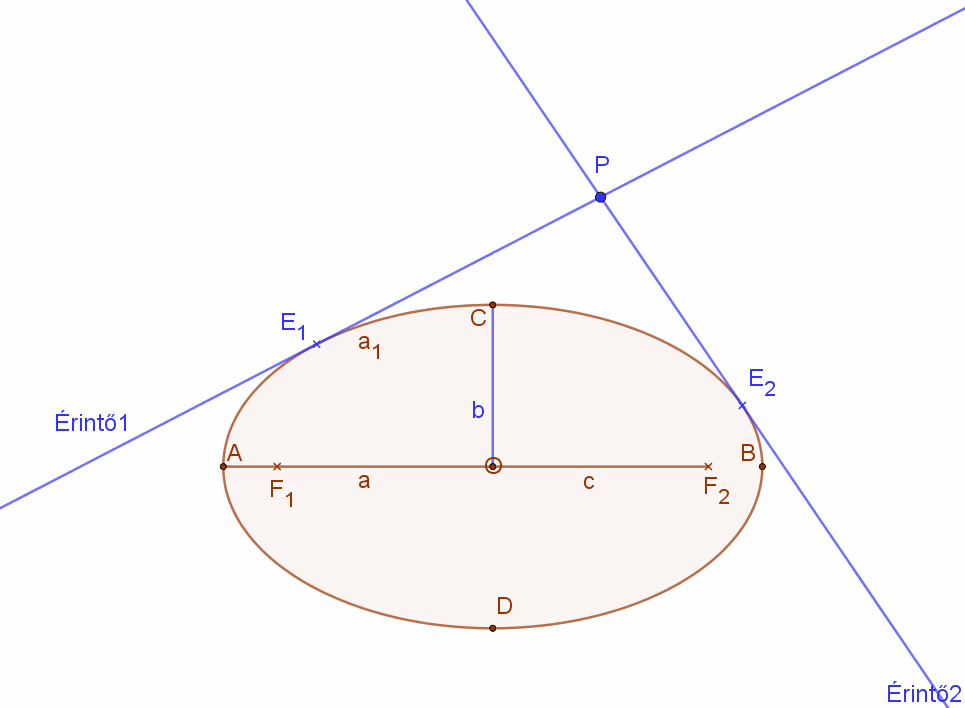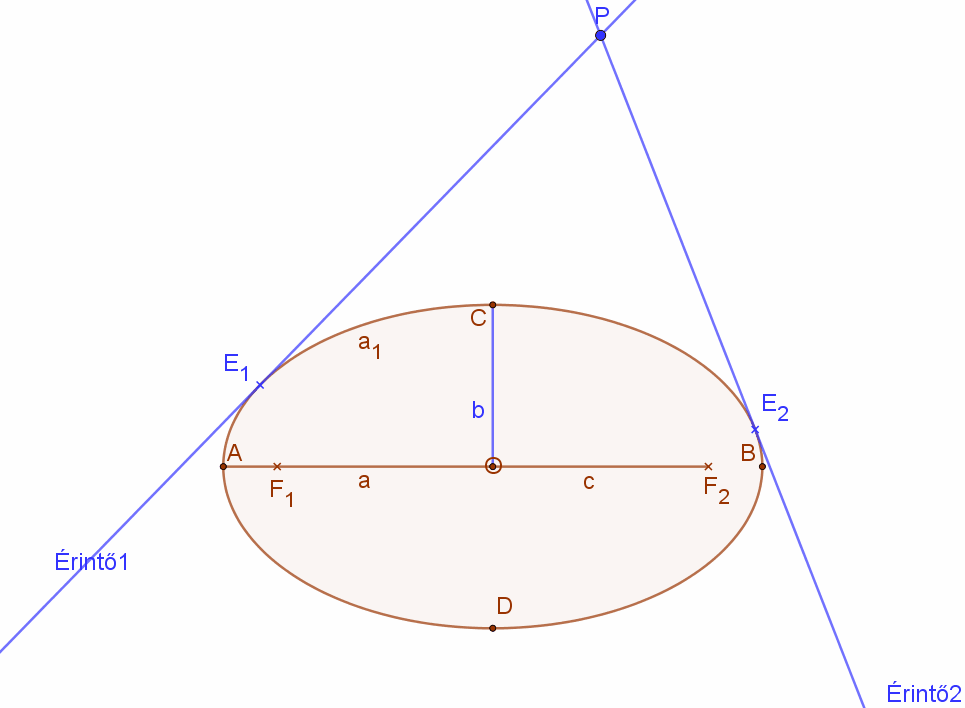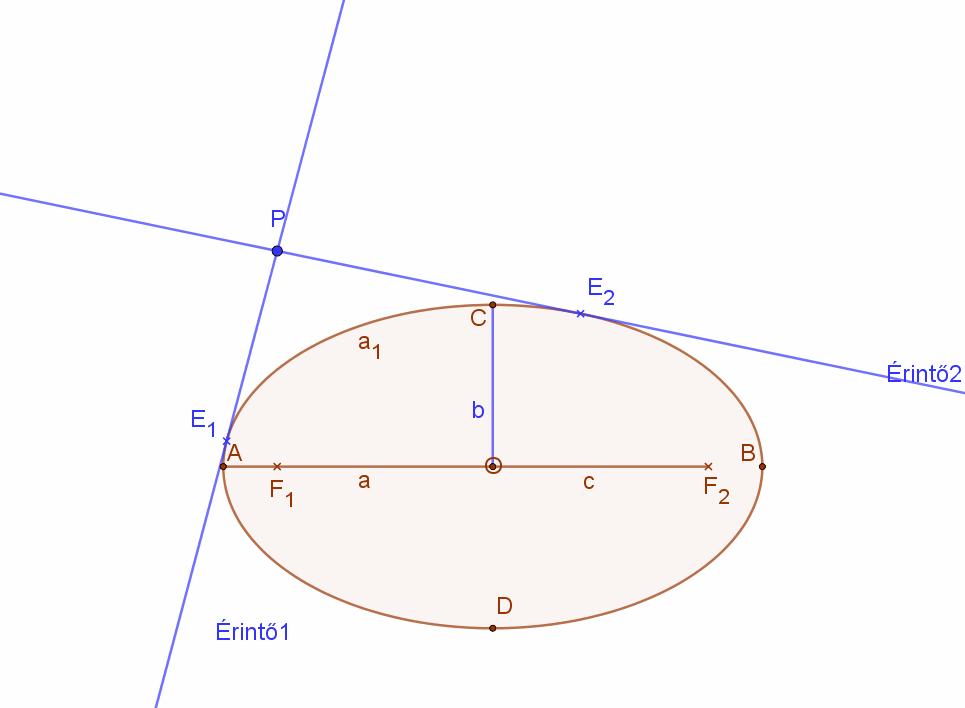
Ellipszishez külső pontból húzott érintők szerkesztése

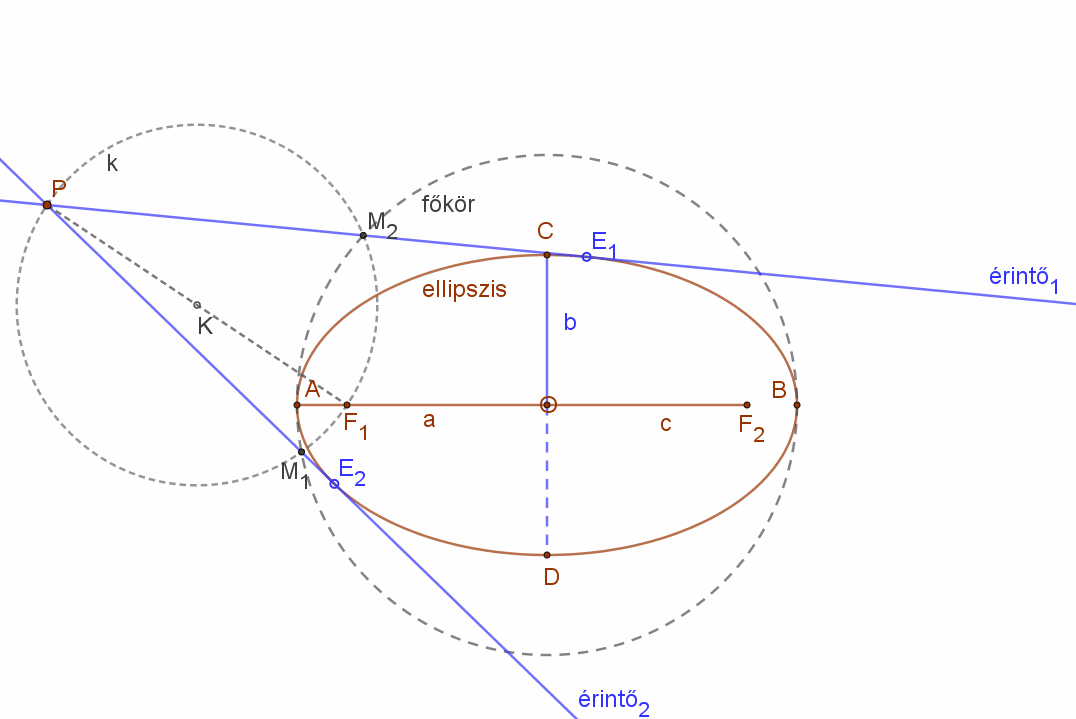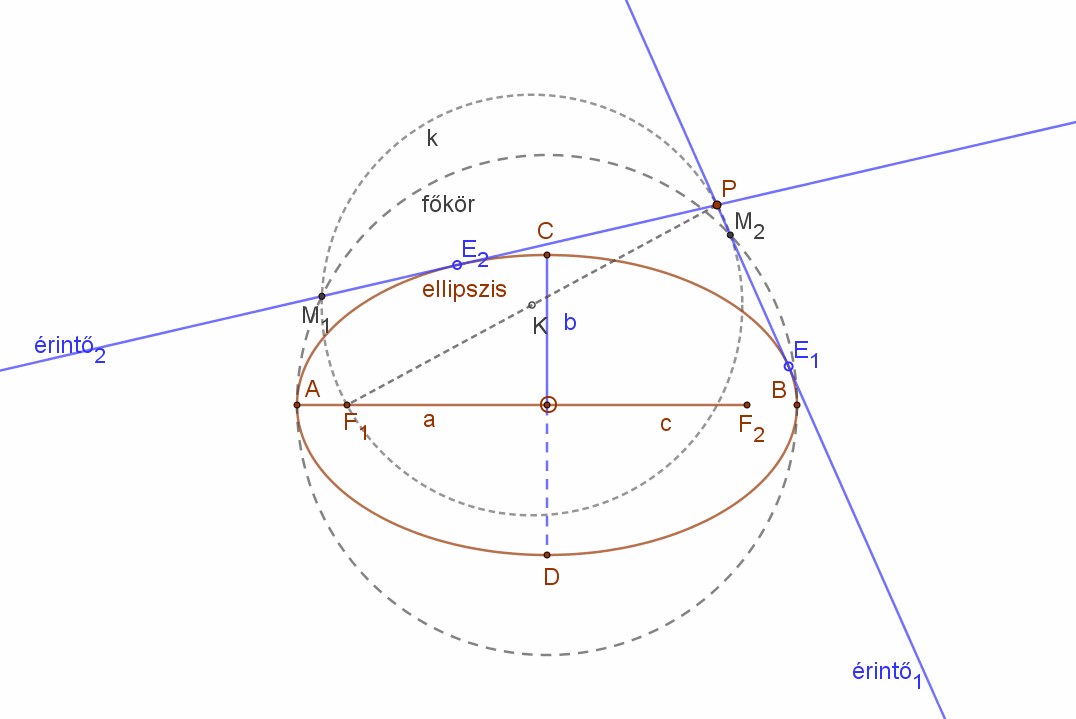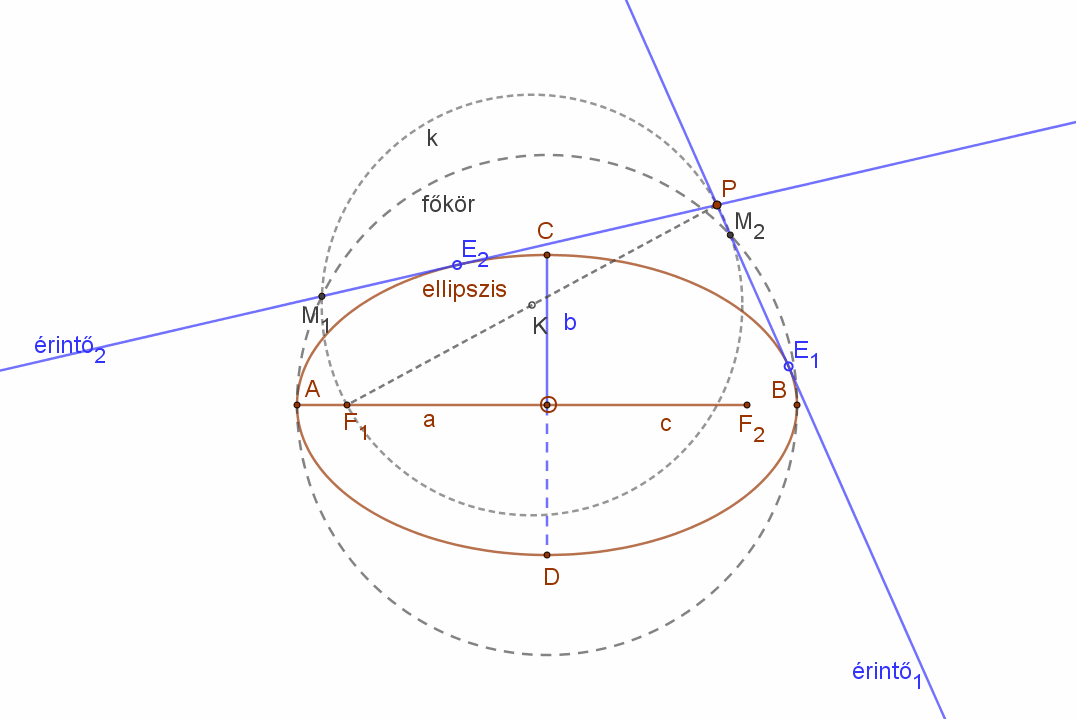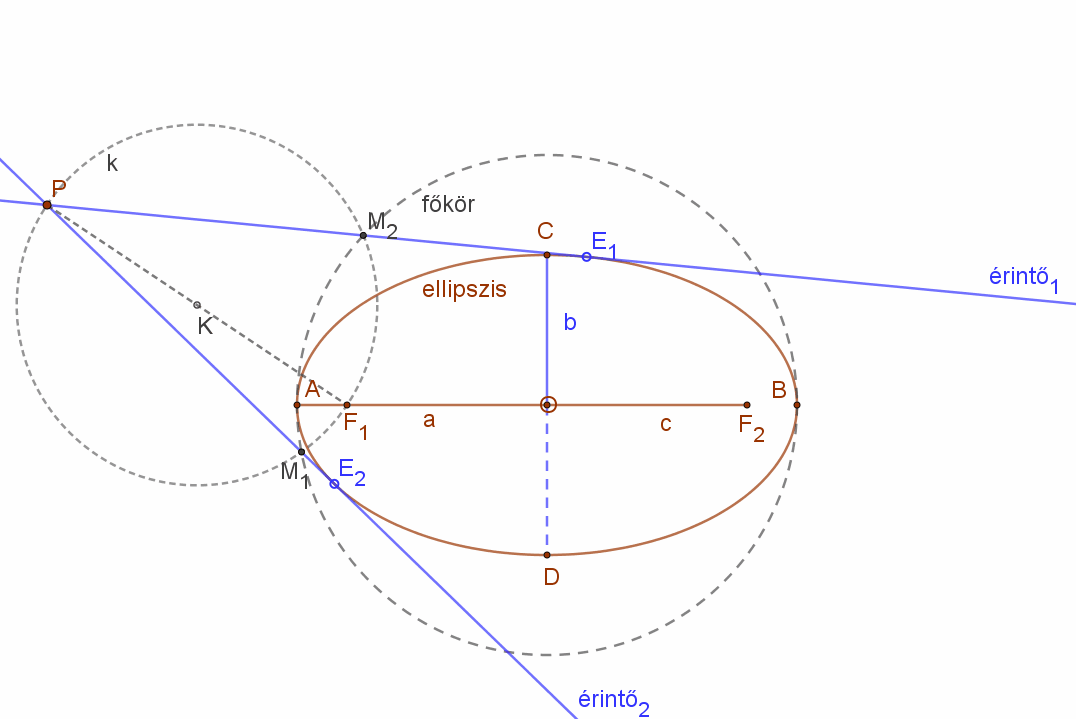
Vegyünk fel egy ellipszist és húzzuk meg az AB nagytengellyel, mint átmérővel az ellipszis un. főkörét. Jelöljünk ki az ellipszis tartományon kívül egy tetszőleges P pontot.
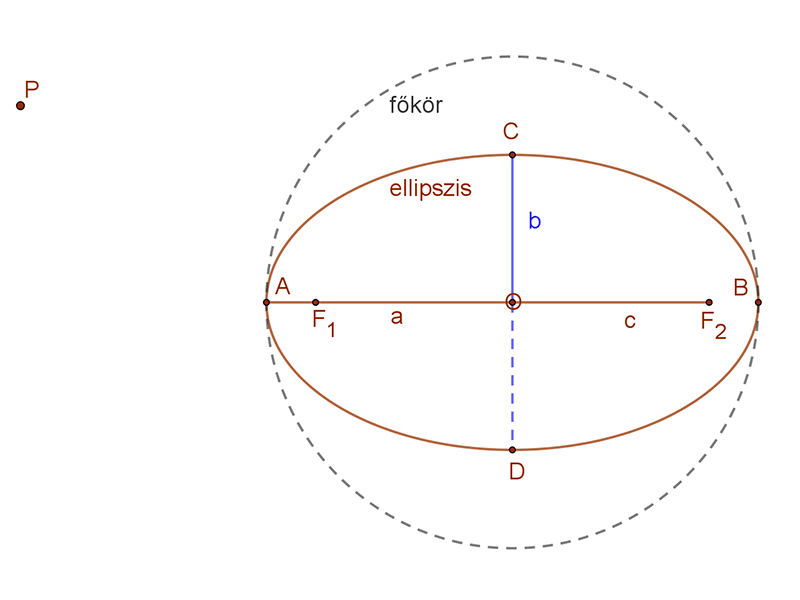Kössük össze a P pontot az ellipszis egyik fókusz pontjával. Ezzel a szakasszal, mint átmérővel húzzunk egy kört (k). Ez a kör két pontban (M1, M2) metszi az ellipszis főkörét.
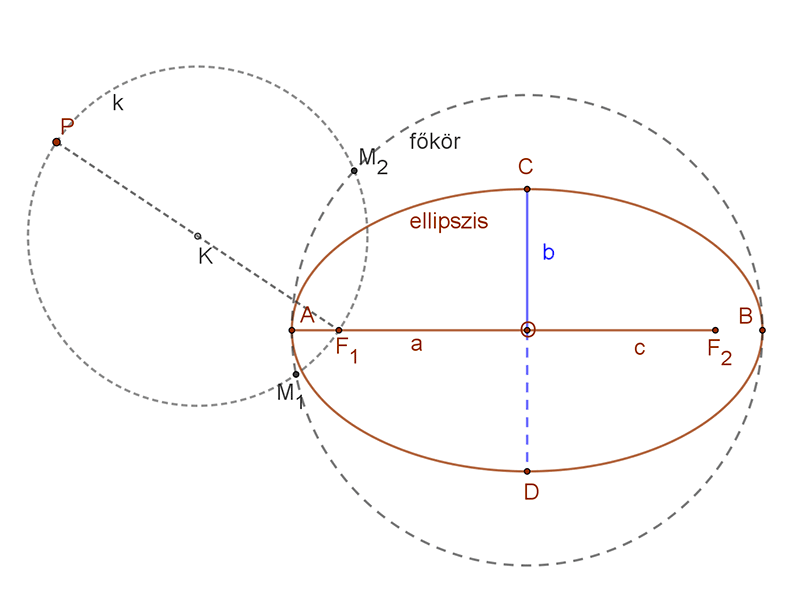A PM1 és PM2 egyenesek az ellipszishez a P pontból húzott érintők egyenesei. Az érintési pontok E1 és E2.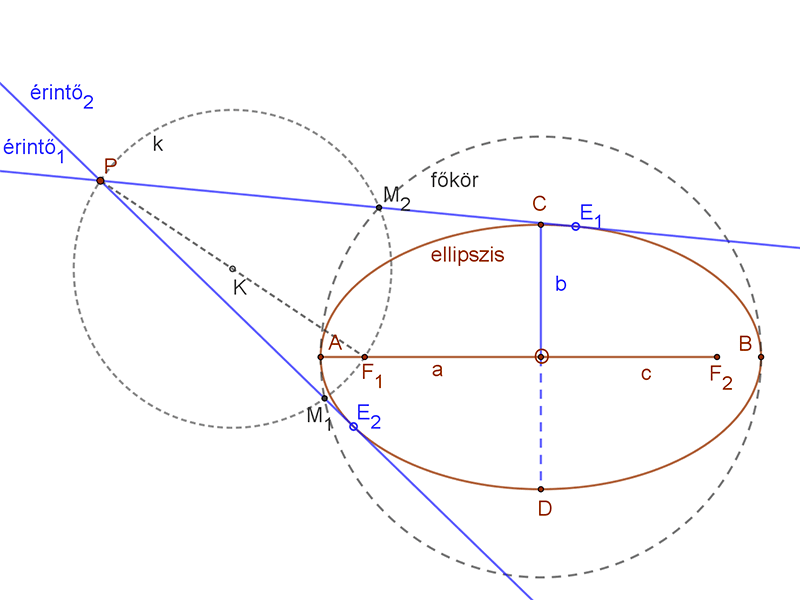

Az ellipszis szerkesztése, szerkeszthetősége

Az ellipszis vonala euklideszi értelemben nem szerkeszthető, de véges számú pontja igen.

Legyen adott egy ellipszis két fókusz pontja. Távolságuk legyen F₁F₂=2c=8 egység. Szerkesztendő annak az ellipszisnek néhány pontja, amelynek pontjai a fókuszoktól való távolságának összege r₁+r₂=10 egység.

Vegyünk fel az F1F2=2c=8 egység hosszúságú szakaszt. Ennek a szakasznak a felezési pontja az „O” pont. Az F1F2 szakasz által meghatározott egyenesre az „O” pontból mérjük ki az a=5 egység távolsággal az „A” és B” pontokat. Az AB=2a szakasz az ellipszis nagytengelye. Az a2=b2+c2 összefogás segítségével a „b” értéke kiszámítható. Így b=3 egység. Az „O” pontban állítsunk merőlegest az F1F2 nagytengelyre. Erre az „O” pontból mérjünk rá a b=3 egység távolságot mindkét irányban. Így kapjuk a C és D pontokat.
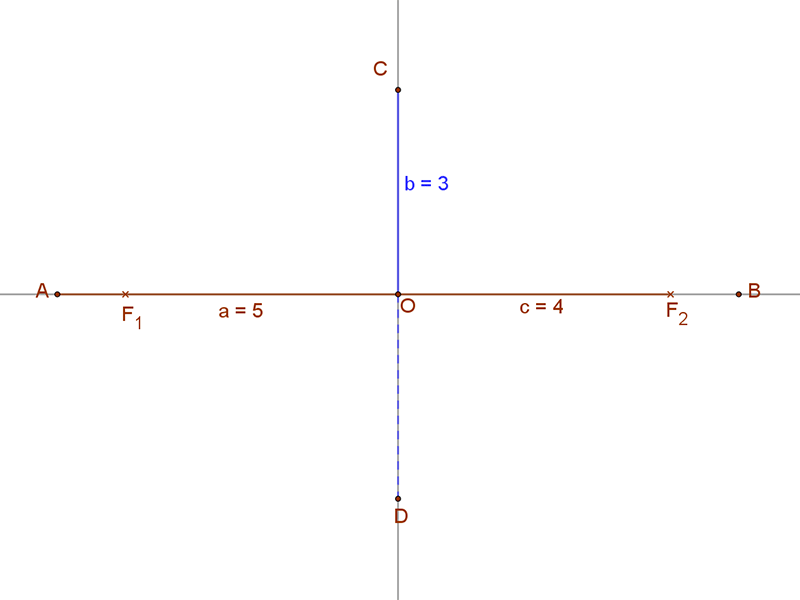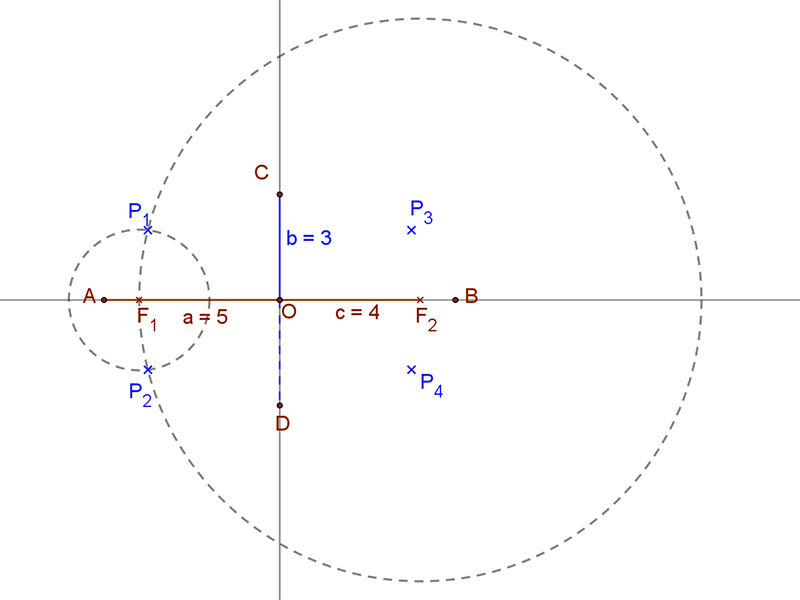
Most szerkesszünk további ellipszis pontokat! A szerkesztés alapja, hogy a fókuszpontok köré egy olyan r1 és r2 sugarú kört húzunk, ahol r1+r2=2a=10. Másképp fogalmazva: bontsuk fel a 2a=10 távolságot két távolság összegére. Ezek metszéspontjai lesznek az ellipszis pontjai. Húzzunk tehát az F1 fókuszpont körül egy r1=2 és az F2 fókuszpont köré egy r2=8 sugarú kört. Ezek metszéspontjai a P1 és P2 pontok. A kapott P1 és P2 pontokat a CD kistengelyre tükrözve a P3 és P4 pontokat is megkapjuk.
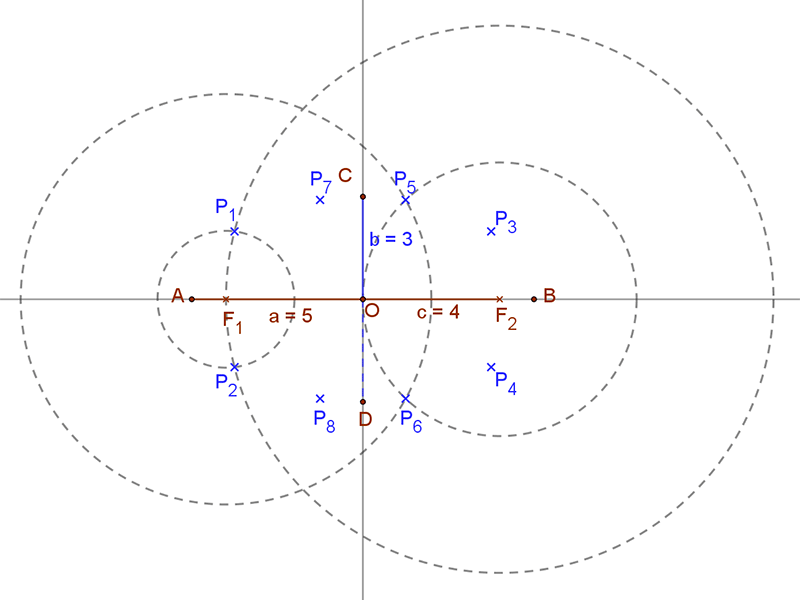
Folytassuk az eljárást! Most egy r1=6 és egy r2=4 sugarú kört húzunk az F1 és az F2 fókuszpontok köré. Ezek metszéspontjai pedig a P5 és P6 pontok. Ezeket a pontokat a CD kistengelyre tükrözve kapjuk a P7 és P8 pontokat.
Így most már megpróbálhatjuk az ellipszis „vonalát” az A, B, C, D, és a P1, P2, P3, P4, P5, P6, P7, P8 pontokon át „meghúzni”.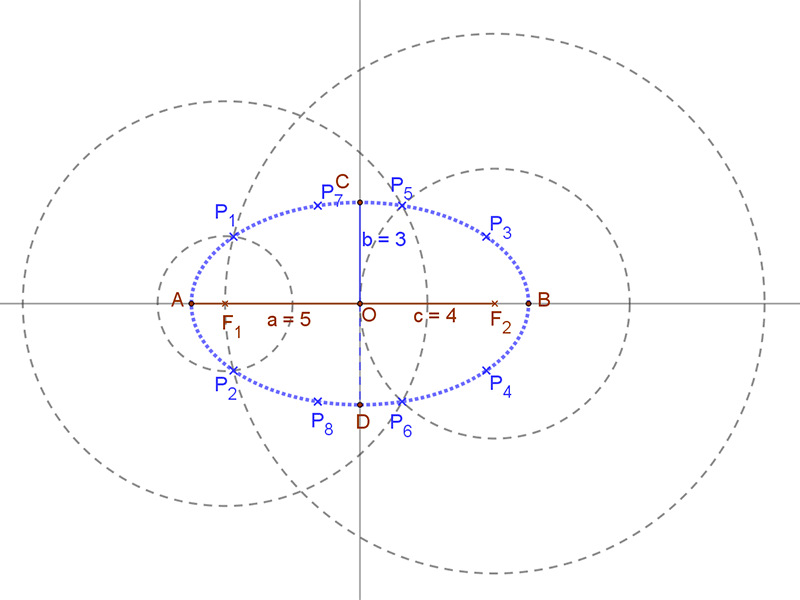
Érdemes berajzolni az egyes pontokhoz tartozó r1 és r2 vezérsugarakat.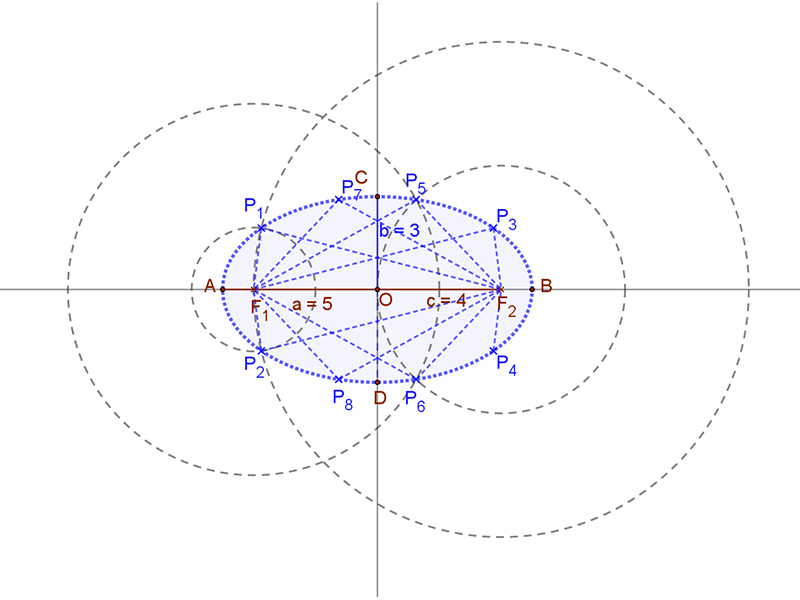

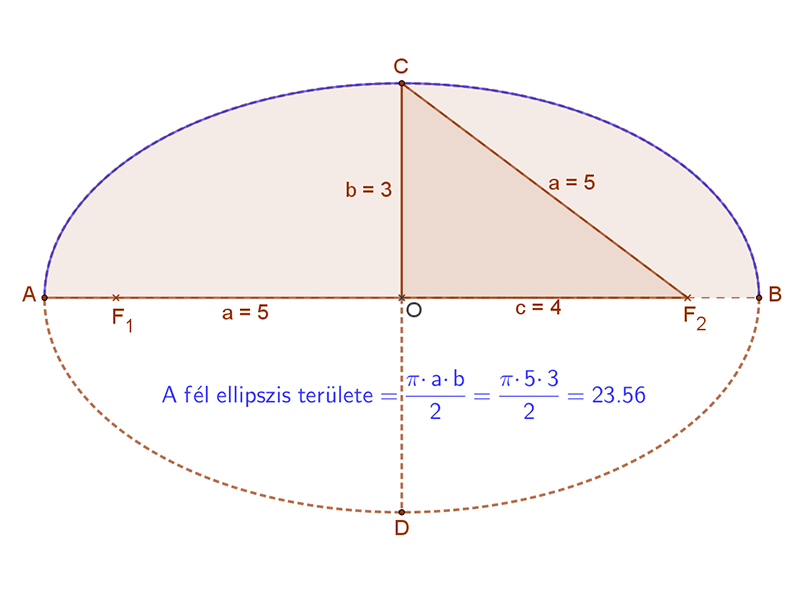
Az ellipszis területe

Az ellipszis területét a ​\( T_{ellipszis}=π·a·b \)​ képlet segítségével számíthatjuk ki,  ahol „a” a nagytengely hosszának a fele,  „b” pedig a kistengely hosszának a fele.

Ha a két fókusz pont egybeesik, akkor a=b, azaz az ellipszis egy r=a=b sugarú kör.
Ez az összefüggés ebben az esetben a kör területének jól ismert képletével, az ​\( r^{2}·π \)​ képlettel azonos.

Az ellipszist azonban kúpszeletként is definiálhatjuk.

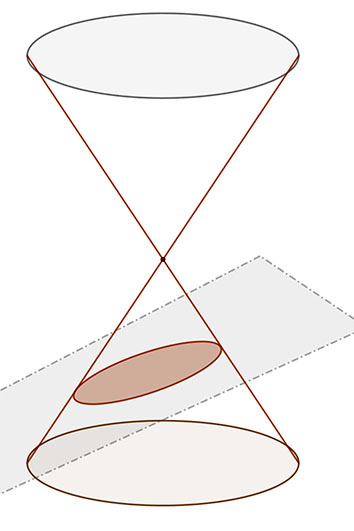
Ha a forgáskúpot olyan síkkal metsszük, amely nem megy át a kúp csúcspontján és a metsző sík nem merőleges a tengelyre, de minden alkotót metsz, akkor a síkmetszet ellipszis. 

A derékszögű koordináta rendszer alkalmazása lehetővé tette az ellipszis analitikus tárgyalását.