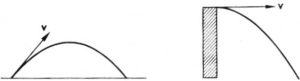
 Közismert, hogy a ferdén vagy vízszintesen elhajított test pályája parabolaív.
Közismert, hogy a ferdén vagy vízszintesen elhajított test pályája parabolaív.
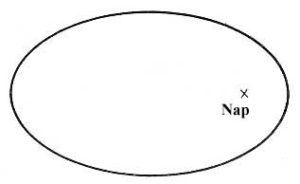
Kepler a XVII. század elején első törvényében megfogalmazta, hogy a bolygók a Nap körül ellipszis pályán keringenek és a Nap az ellipszis egyik fókuszpontjában van.
Ma már elemi fizikai ismeretnek számít, hogy a Földről fellőtt rakéták, űrhajók pályája az indítási sebességtől függ.
A rakéta pályája lehet olyan ellipszis, melynek a fellövési helytől számított távolabbi fókuszpontja a Föld középpontja.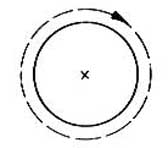
A műhold pályája lehet kör.
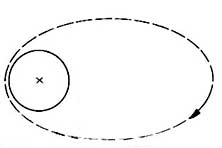
Az űrhajó pályája lehet olyan ellipszis, melynek a fellövési helytől számított közelebbi fókuszpontja a Föld középpontja.
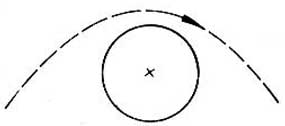
A rakéta pályája lehet olyan hiperbola, amelynek egyik fókuszpontja a Föld középpontja.
A körrel, az ellipszissel, a parabolával és a hiperbolával már, mint nevezetes ponthalmazokkal eddig is találkozhattunk.
A fenti fizikai tények is azt mutatják, hogy ezek a görbék rokonságban vannak egymással.
Ha egy forgáskúpot olyan síkkal metszünk, amely nem megy át a kúp csúcspontján, akkor a metsző síknak a dőlésszögétől függően más-és más síkmetszetet kapunk.
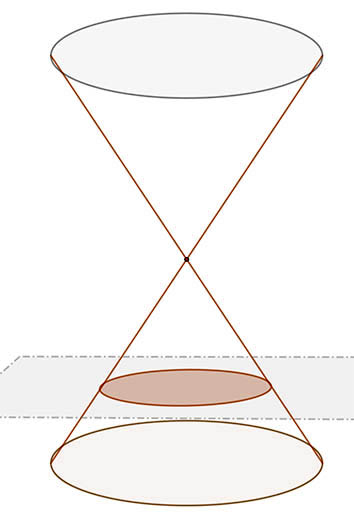 Ha a metsző sík merőleges a tengelyre, akkor a síkmetszet kör.
Ha a metsző sík merőleges a tengelyre, akkor a síkmetszet kör.
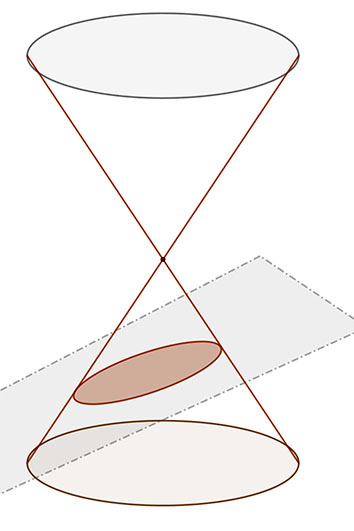
Ha a metsző sík nem merőleges a tengelyre, de minden alkotót metsz, akkor a síkmetszet ellipszis.
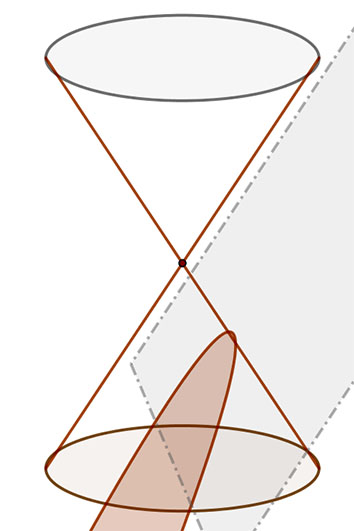
Ha a metsző sík egy alkotóval párhuzamos, akkor a síkmetszet parabola.
Ha a metsző sík két alkotóval párhuzamos, akkor a síkmetszet hiperbola.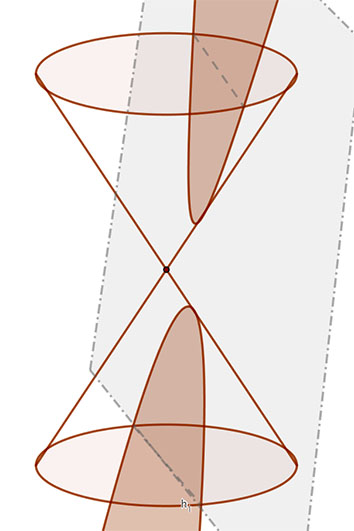
Történelmi előzmények:
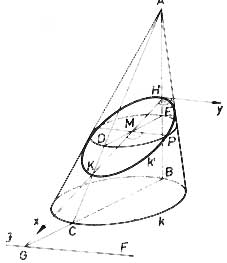
Már az ókorban felismerték ezt. Több görög matematikus írt róluk. Elsősorban Apollóniosz 8 kötetes „Kúpszeletek” című műve a legalaposabb tárgyalása ennek a témának Az elnevezés is tőle származik.
Ő a kúpszeleteket egy ferde kettős körkúp síkmetszeteiként tárgyalta. Mivel mindent a kúpszeletek átmérőire vonatkoztatott, ez már a koordináta-geometria tárgyalás irányába mutat. A mellékelt ábra jól mutatja ezt. A matematikusok évszázadokon át nem tudták ezt a tárgyalási módot túlhaladni. Az első mű, amiben ez sikerült, Euler „Introductio”-ja (Bevezetés) volt.
A derékszögű koordináta rendszer alkalmazása lehetővé tette a kör, a parabola, az ellipszis, és a hiperbola analitikus tárgyalását.
A kúpszeletek forgatásaiból adódó testek térfogatait elsőként Arkhimédész számította ki. Ugyanezt tette Kepler 1615-ben megjelent „Stereometria doliorum vinorum” (A boroshordók térgeometriája) című művében.


Comments are closed, but trackbacks and pingbacks are open.