Kepler életéről:

Német csillagász, fizikus és matematikus. Evangélikus egyházi iskolában végzett, és teológiát is tanult. 1594-ben, Grazban matematikát tanított. Feltűnő tehetsége miatt Tycho Brahe csillagász professzor 1600-ban Prágába hívta, ahol Brahe halála után Kepler lett a császári csillagász, majd később udvari matematikus. A kopernikuszi heliocentrikus világképet igazolta munkásságával. Kepler az optikát is új felfedezésekkel gazdagította. 1611-ben kifejlesztett egy új csillagászati távcsövet. „Optika” című műve a fiatal Newtonra is nagy hatással volt.Kepler mély vallásossága következtében a természet kutatását a Teremtő műve iránti szolgálatnak tekintette.
Közismertek a bolygók mozgására vonatkozó törvényei:
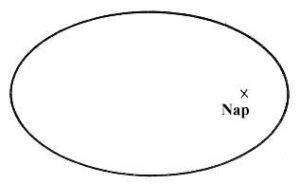 A bolygók a Nap körül ellipszis alakú pályán keringenek, amelynek egyik fókuszpontjában a Nap van.
A bolygók a Nap körül ellipszis alakú pályán keringenek, amelynek egyik fókuszpontjában a Nap van.- A vezérsugár (amely a bolygót és a Napot köti össze) egyenlő idők alatt egyenlő területeket súrol.
- Két bolygó keringési idejének négyzetei úgy aránylanak egymáshoz, mint a Naptól számított középtávolságaik. (az ellipszispályáik fél nagytengelyeinek) a köbei.
Kepler matematikai munkásságáról:
1615-ben megjelent „Stereometria doliorum vinorum” („A boroshordók térgeometriája”) című művében Arkhimédészhez hasonlóan, azt továbbfejlesztve a kúpszeletek forgatásaiból adódó testek térfogatait számította ki, evvel is jelentősen elősegítette az integrálszámítás felfedezését. Ebben a művében 92 db. különböző forgástest térfogat számítását ismertette.
Egyik ma is megoldatlan probléma Kepler gömbelhelyezési problémája. 1611-ben jelent meg „Hatszögletű hópelyhekről” szóló tanulmánya. Ebben Kepler leírja, hogy minden hópehely másféleképpen néz ki, de mind hatszögletű. Ez avval magyarázható, hogy minden hópehely élete egy hatszögletű szimmetrikus maggal kezdődik. Az állandóan változó időjárási feltételek teszik egyedivé, a hópehely magja azonban olyan parányi, hogy a növekedést meghatározó feltételek ugyanazok lesznek mind a hat oldalon, így fenntartják a szimmetriát. Ebben a tanulmányban Kepler megvetette a kristálytan alapjait.
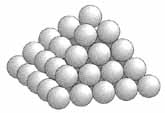 Kepler ezek után avval a kérdéssel kezdett el foglalkozni, hogy milyen módon rendeződhetnek el a gömb alakú részecskék a lehető leggazdaságosabban, a lehető legkisebb teret elfoglalva. Kepler szerint az un. lapcentrált kockarács a lehető leggazdaságosabb elrendezés, amely a mellékelt ábrán látható. Ez az elrendezés 74%-os kihasználtságot biztosít. Ma sem tudják a matematikusok bizonyítani, hogy ez az elrendezés minden lehetséges elrendezés közül a legjobb. Kepler használt először tizedesvesszőt. (Napier pedig tizedespontot.)
Kepler ezek után avval a kérdéssel kezdett el foglalkozni, hogy milyen módon rendeződhetnek el a gömb alakú részecskék a lehető leggazdaságosabban, a lehető legkisebb teret elfoglalva. Kepler szerint az un. lapcentrált kockarács a lehető leggazdaságosabb elrendezés, amely a mellékelt ábrán látható. Ez az elrendezés 74%-os kihasználtságot biztosít. Ma sem tudják a matematikusok bizonyítani, hogy ez az elrendezés minden lehetséges elrendezés közül a legjobb. Kepler használt először tizedesvesszőt. (Napier pedig tizedespontot.)


Comments are closed, but trackbacks and pingbacks are open.