A Pitagorasz tétel a geometria, sőt talán a matematika egyik legközismertebb tétele, amely a derékszögű háromszög oldalai közötti összefüggést mondja ki.
Pitagorasz tétele:
A derékszögű háromszög befogóira emelt négyzetek területeinek összege egyenlő az átfogóra emelt négyzet területével.
A mellékelt ábra jelölései szerint: a2+b2=c2.
A tétel bizonyítása:
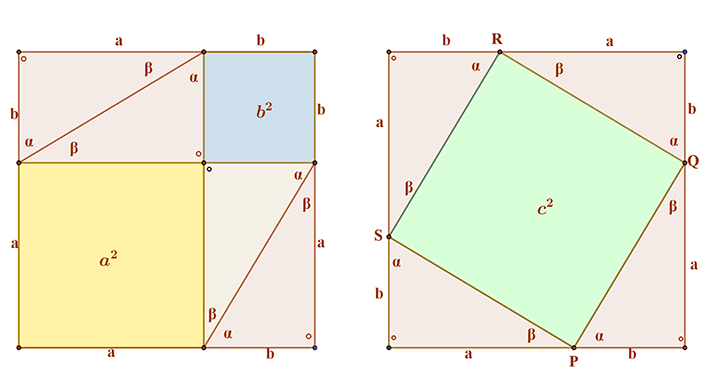
Készítsünk két darab (a+b) oldalú négyzetet az alábbi módokon, ahol „a” és „b” a derékszögű háromszög befogói! (Ez a „csel”.) A két darab (b+a) oldalú négyzetek területe nyilvánvalóan egyenlő.
A tétel bizonyításában felhasználjuk azt az euklideszi axiómát, hogy „Ha egyenlőkből egyenlőket veszünk el, akkor a maradékok is egyenlők.”
|
|
|
| A fenti baloldali négyzetben kaptunk 4 darab, az eredeti háromszöggel egybevágó derékszögű háromszöget, és egy „a” illetve „b” oldalú négyzetet. Ezek területe a2 és b2 területegység. | A jobboldali négyzetben is megtalálható ez a 4 darab, az eredeti háromszöggel egybevágó derékszögű háromszög, amelynek átfogója „c„. Így tehát a középső PQRS síkidom minden oldala „c”. Be kell még látni, hogy csúcsainál derékszög van. Mivel azonban az eredeti háromszögben α+β=90°, ezért ennek a síkidomnak minden szögére 180°-(α+β )=90°. Tehát a PQRS síkidom négyzet, területe pedig c2. |
Ha mindkét négyzetből elvesszük a 4 darab derékszögű háromszöget, a maradékok területe is egyenlő, azaz a2+b2=c2.
A tétel megfordítása:
Ha egy háromszög két oldalára emelt négyzetek területének összege egyenlő a harmadik oldalra emelt négyzet területével, akkor a háromszög derékszögű.
Bizonyítás:
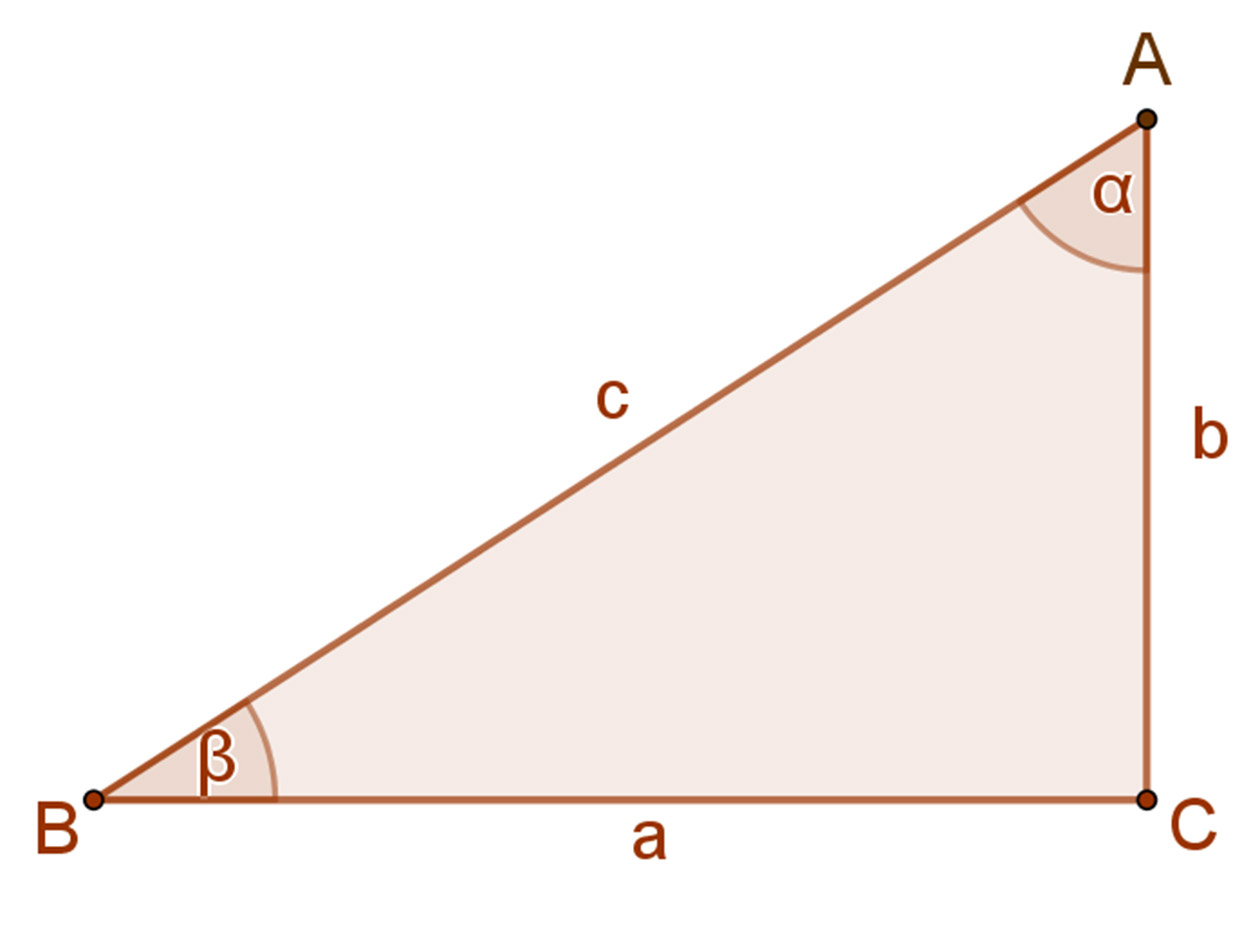Legyen adott egy ABC háromszög, amelynek oldalaira teljesül, hogy két oldalára emelt négyzetek területének összege egyenlő a harmadik oldalra emelt négyzet területével. A mellékelt ábra jelölései szerint: a2+b2=c2. Be kell bizonyítani, hogy az ABC háromszög derékszögű.
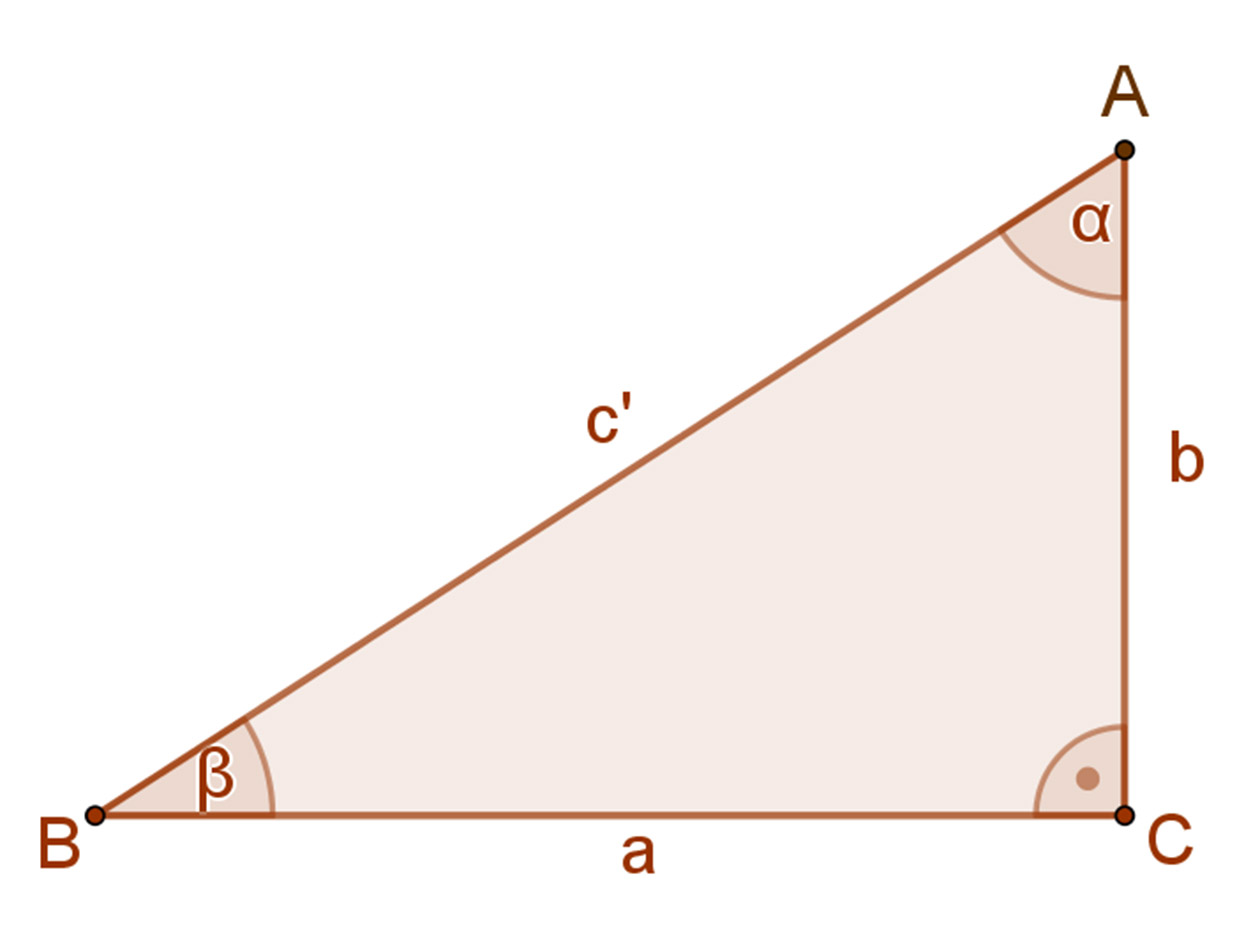Vegyünk most fel egy „a” és „b” befogójú derékszögű háromszöget. Ennek átfogóját jelöljük „c’„-vel. Erre a háromszögre teljesül a Pitagorasz-tétel, tehát a2+b2=c‘2.
A két összefüggés csak akkor lehet egyszerre igaz, ha c2=c‘2.
Ez viszont azt jelenti, hogy a két háromszög egybevágó, tehát az eredeti ABC háromszög is derékszögű.
Az összefüggés a befogó tétel, a szelő tétel vagy a koszinusz tétel segítségével is bizonyítható, de ezeken kívül is számos bizonyítása ismeretes még.
Tétel alkalmazása:
- Ha adott egy derékszögű háromszög két oldala, a tétel segítségével kiszámítható a harmadik oldal hossza.
- Ha adott egy derékszögű háromszög három oldala, akkor a tétel segítségével eldönthető, hogy a háromszög szögei szerint milyen: hegyesszögű, derékszögű vagy tompaszögű. Jelöljük „c”-vel a háromszög leghosszabb oldalát. Pontosabban: „c” jelölje azt oldalt, amelynél nincs nagyobb oldala a háromszögnek.
| Ha egy ilyen háromszögben a2+b2>c2, akkor a háromszög hegyesszögű. | Ha egy ilyen háromszögben a2+b2=c2, akkor a háromszög derékszögű. | Ha egy ilyen háromszögben a2+b2 <c2, akkor a háromszög tompaszögű. |
 |
||
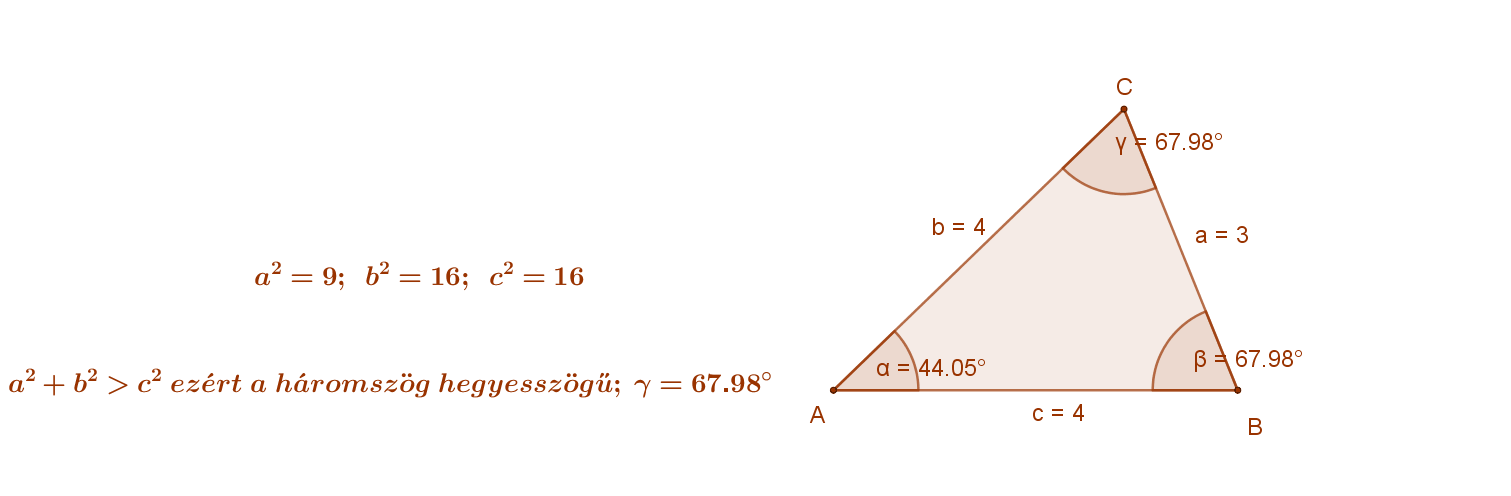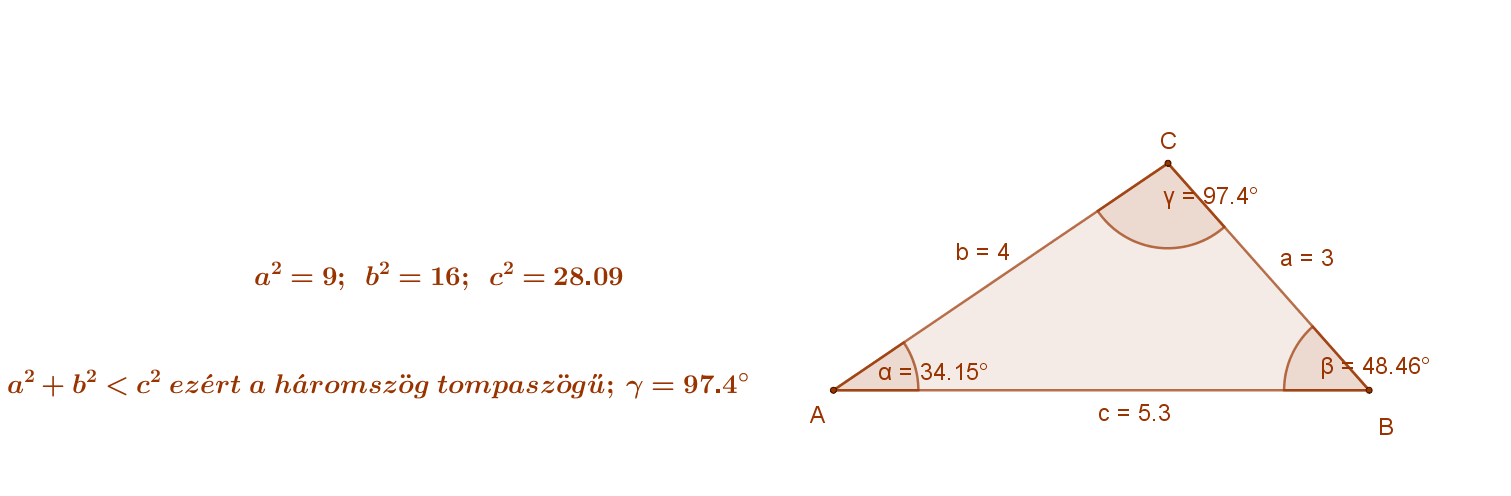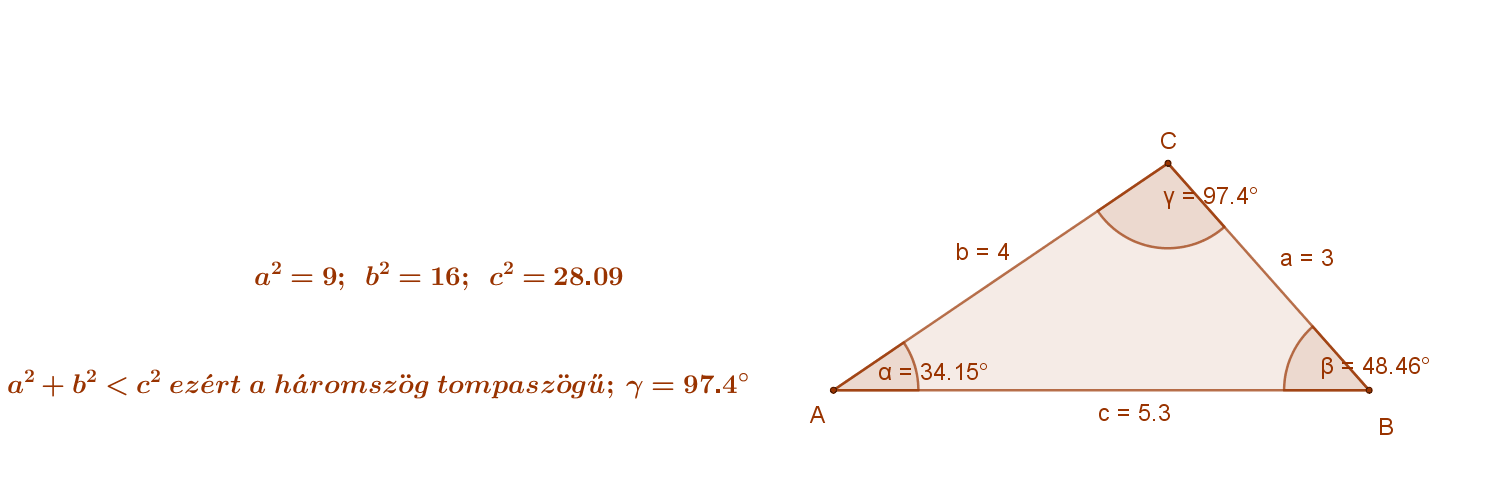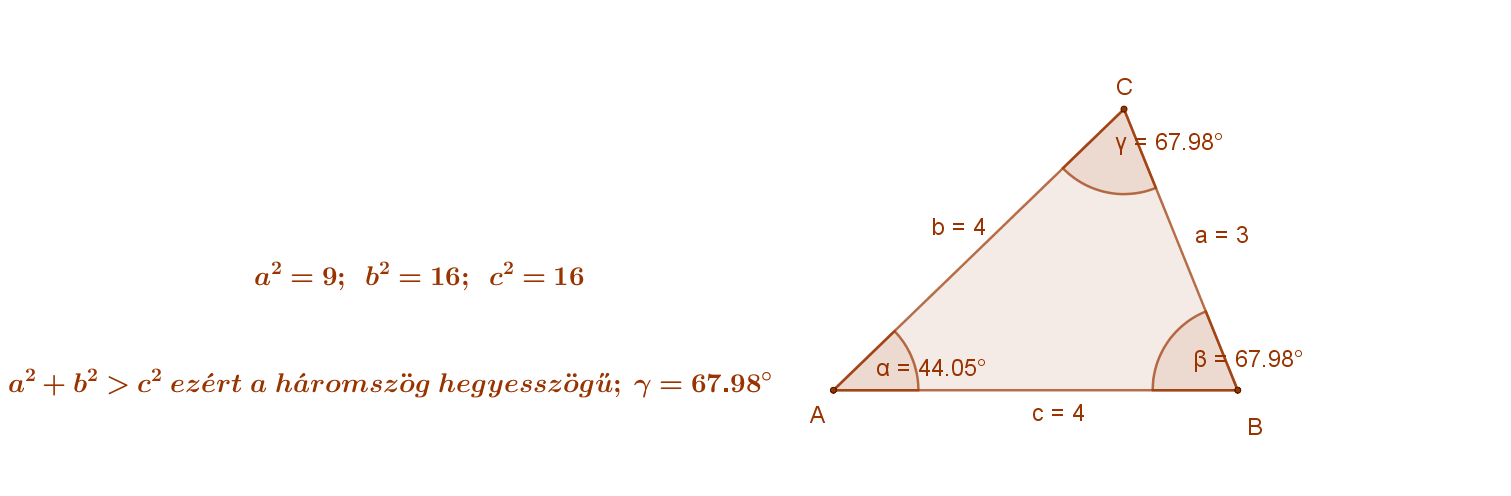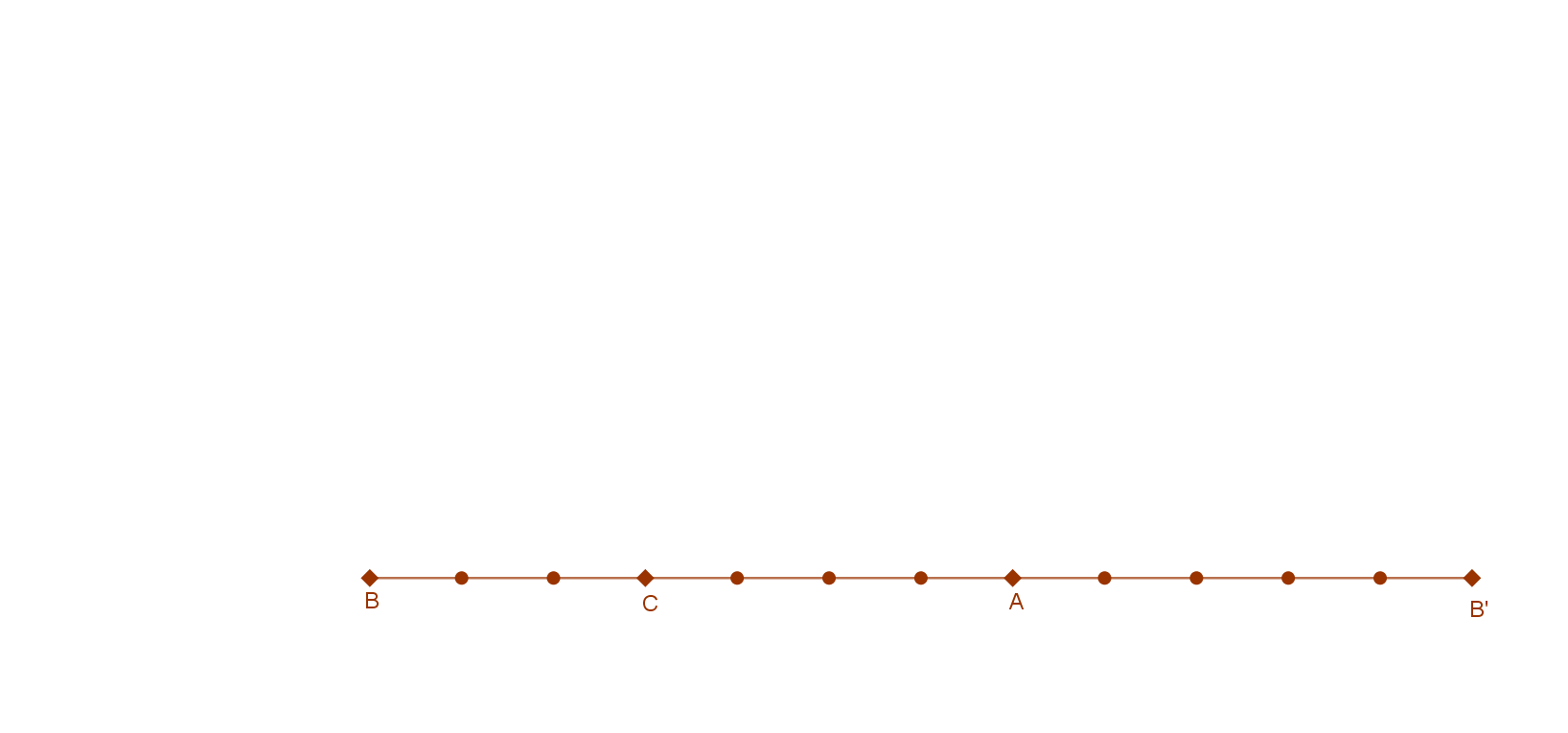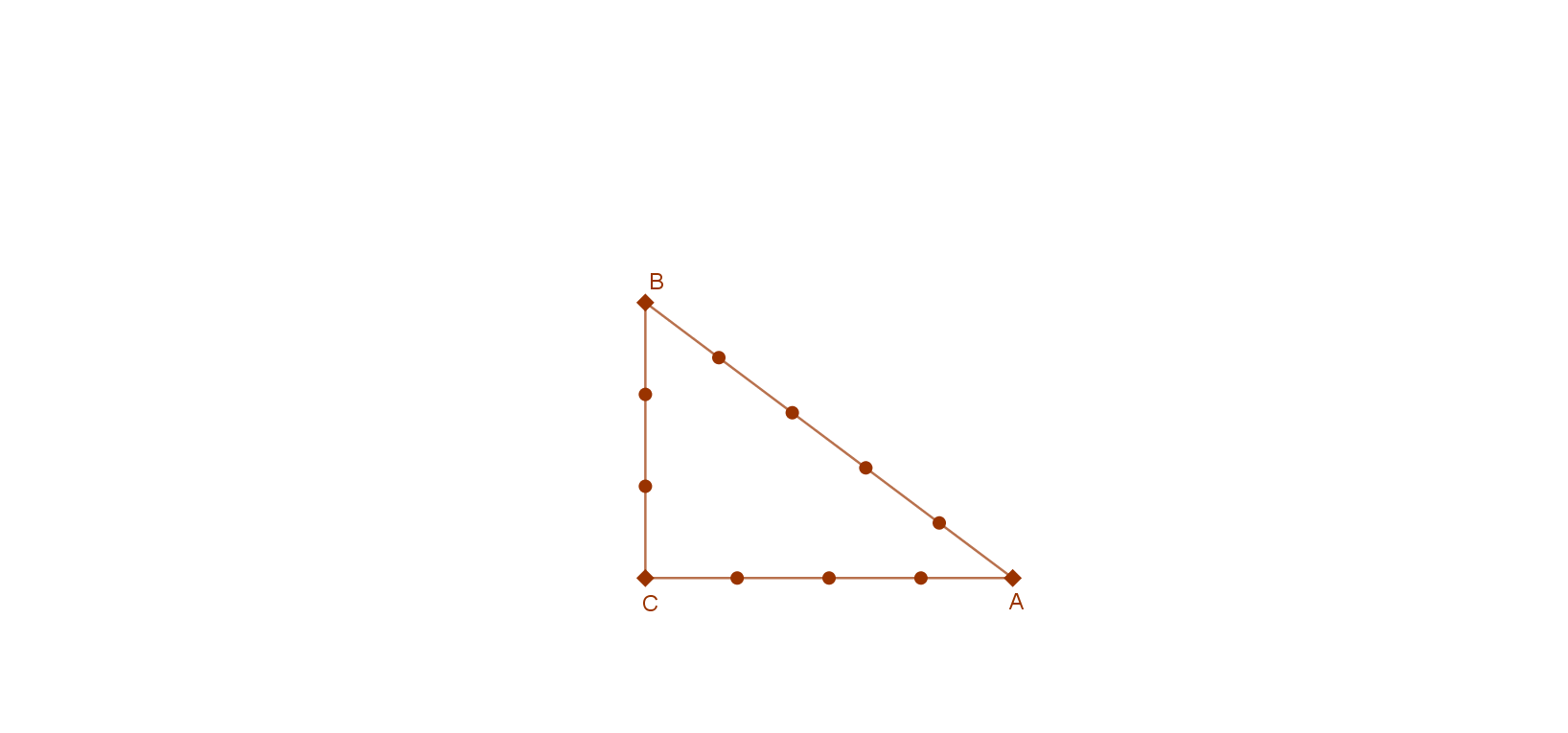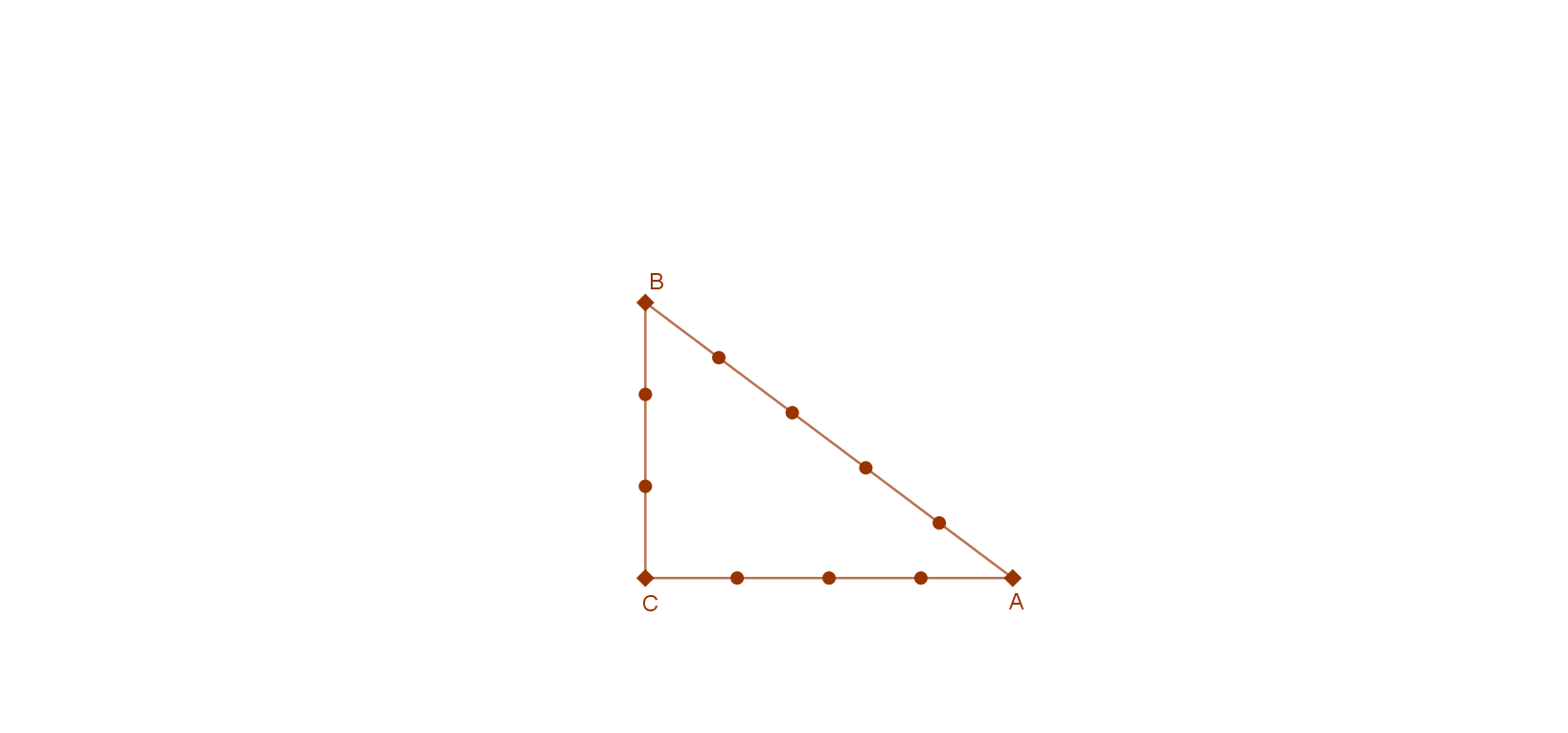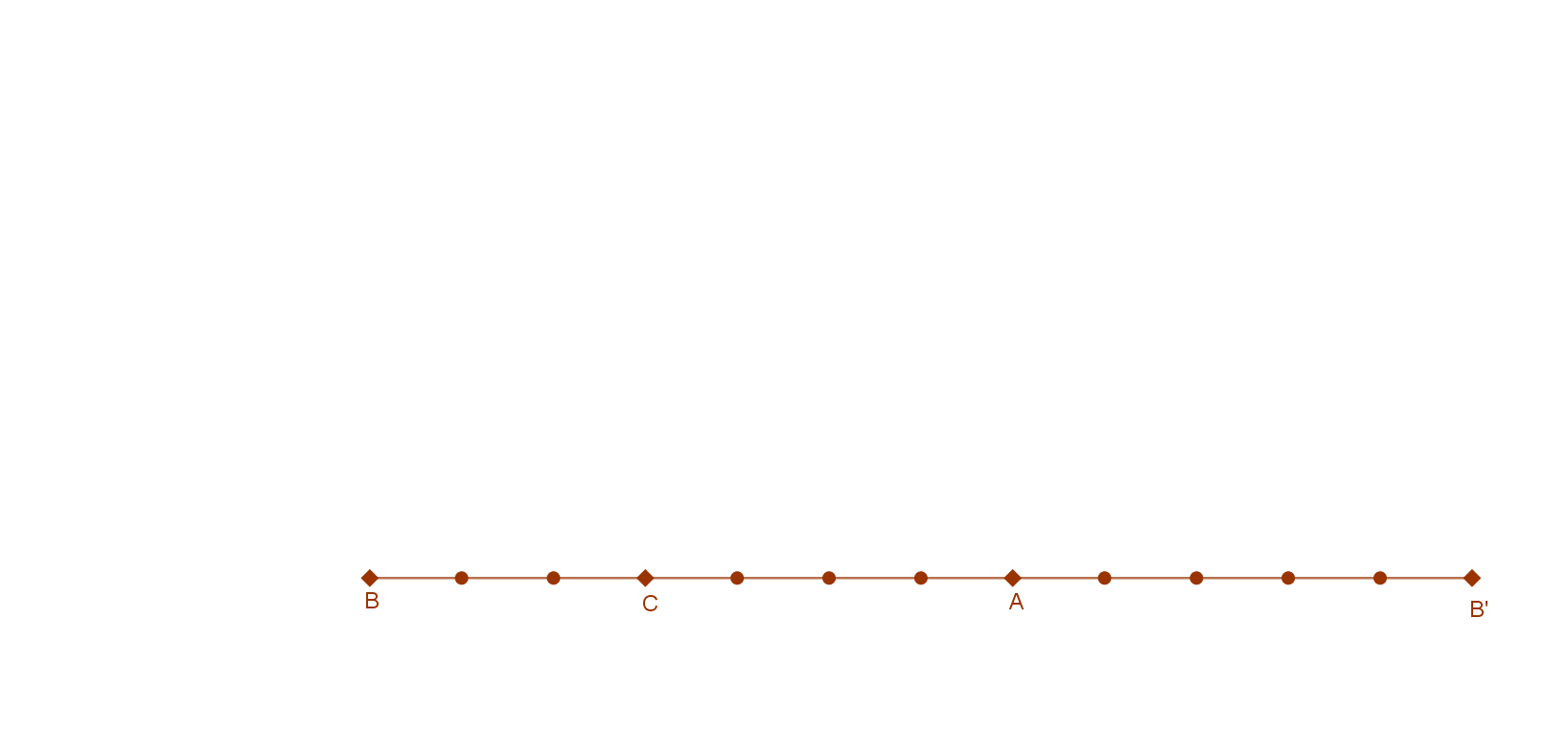Már az ókorban is a ennek a tételnek a segítségével hoztak létre derékszöget anélkül, hogy a tételt általánosságban kimondták volna. Ez természetesen alapvető fontosságú volt például az építkezéseken, bútorok készítésében és még sok más esetben is. Az egyiptomiak csomókkal 3, 4 és 5 részre osztott kötelet használták a derékszög előállítására. Ehhez összesen 13 darab egyforma távolságban kötött csomóra volt szükségük. Így egy olyan derékszögű háromszög jött létre, amelynek oldalai megfelelnek a Pitagorasz tételnek, hiszen \( 3^{2}+4^{2}=5^{2} \). Ez a 3; 4; 5 számhármas egy un. Pitagoraszi számhármas.
A tételt már ismerték Pitagorasz előtt is. Például az egyiptomi Rhind-papiruszon szerepel egy 3; 4; 5 oldalú háromszög. A babilóniai agyagtábla pitagoraszi számhármasokat tartalmaz. Úgy tudjuk, a tételt Pitagorasz bizonyította elsőként.
Feladat:
Szerkesszünk egy egységnyi befogójú egyenlőszárú derékszögű háromszöget és számítsuk ki az átfogó hosszát!
Majd ennek a háromszög átfogójának egyik végpontjában emeljünk merőlegesen egy egységnyi hosszúságú szakaszt! Így kapott pontot összekötve átfogó másik végpontjával, kapunk egy újabb derékszögű háromszöget. Határozzuk meg ennek az átfogónak a hosszát!
Megoldás:
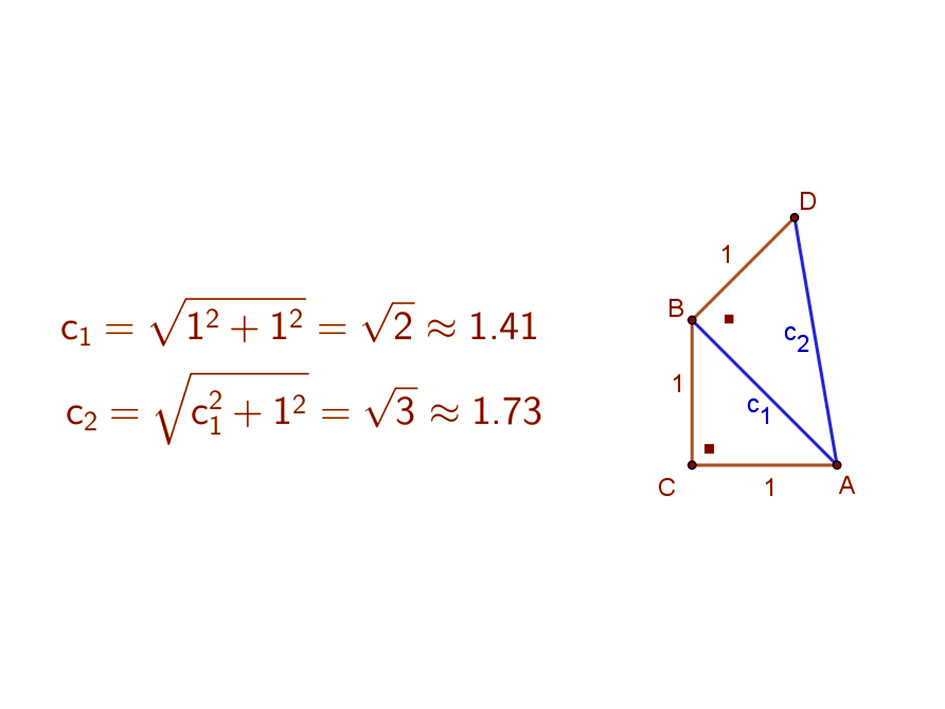Az ABC egyenlőszárú derékszögű háromszög AB (c1) átfogóját a Pitagorasz tétel segítségével tudjuk kiszámítani: \( c_1^{2}=1^{2}+1^{2}=2 \). Így \( c_1=\sqrt{2}≈1.41 \).
A B pontban emelt egységnyi hosszúságú szakasz D végpontját összekötve az eredeti háromszög A pontjával, kapjuk az ABD derékszögű háromszöget, amelynek egyik befogója egységnyi, a másik befogója az eredeti háromszög AB átfogója amelynek hossza \( c_1=\sqrt{2}≈1.41 \). Ennek az ABD derékszögű háromszögnek az átfogóját szintén a Pitagorasz tétel segítségével kiszámolva: \( c_{2}^2=\sqrt{2}^{2}+1^{2}=3 \). Így \( c_{2}=\sqrt{3}≈1.73 \). Lásd a mellékelt ábrát!
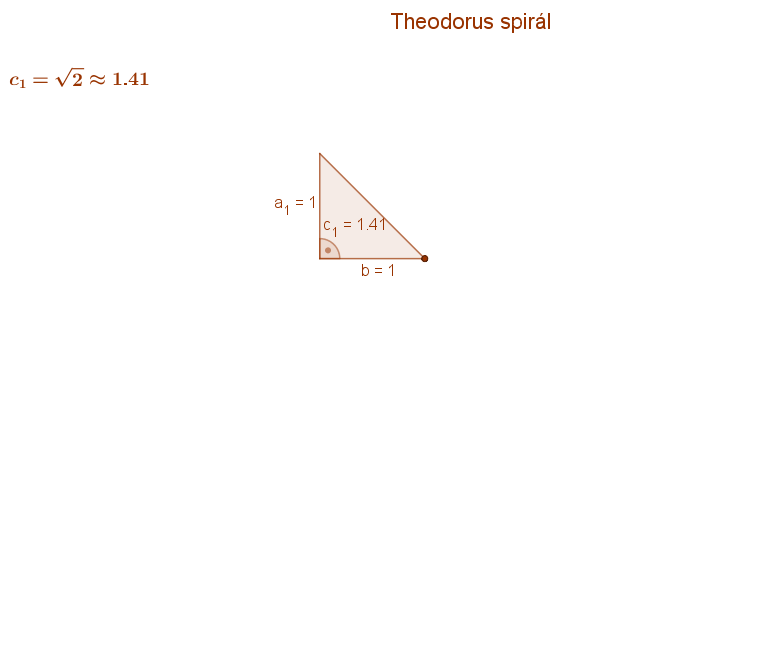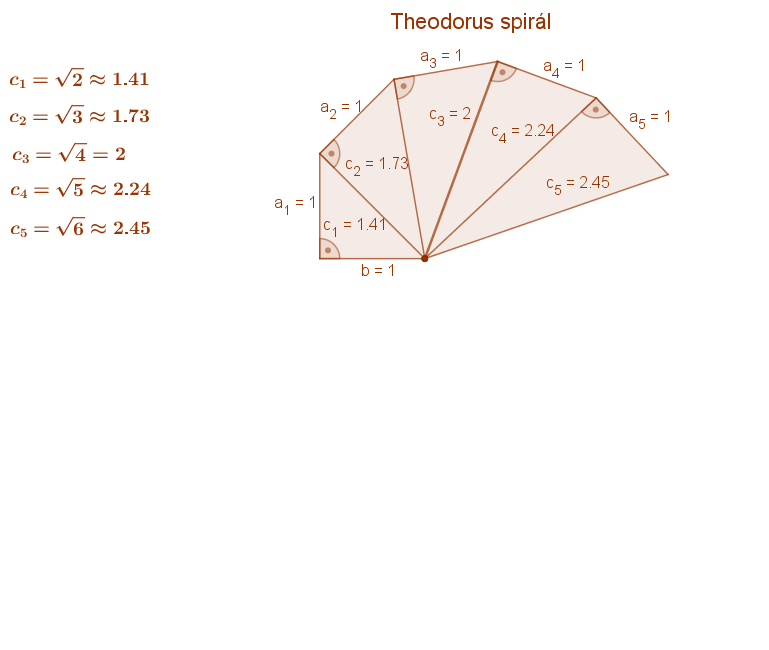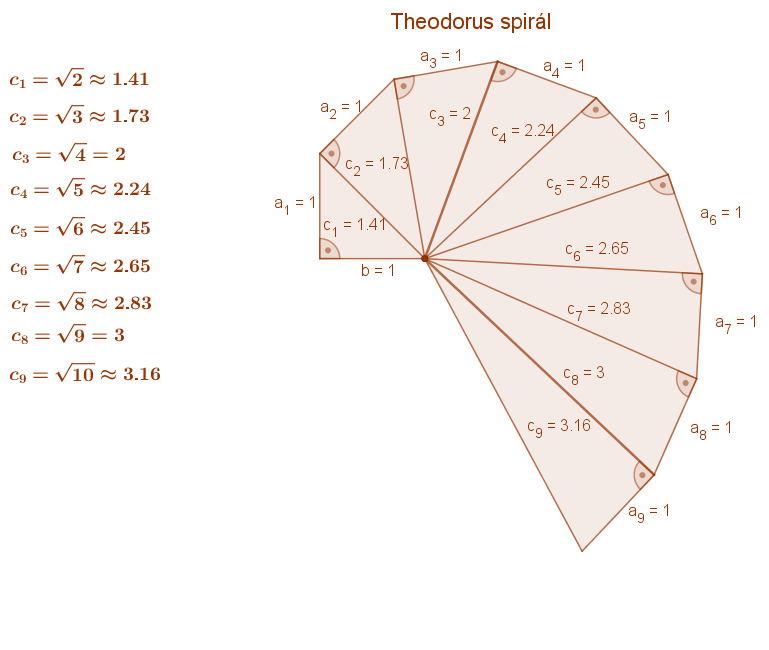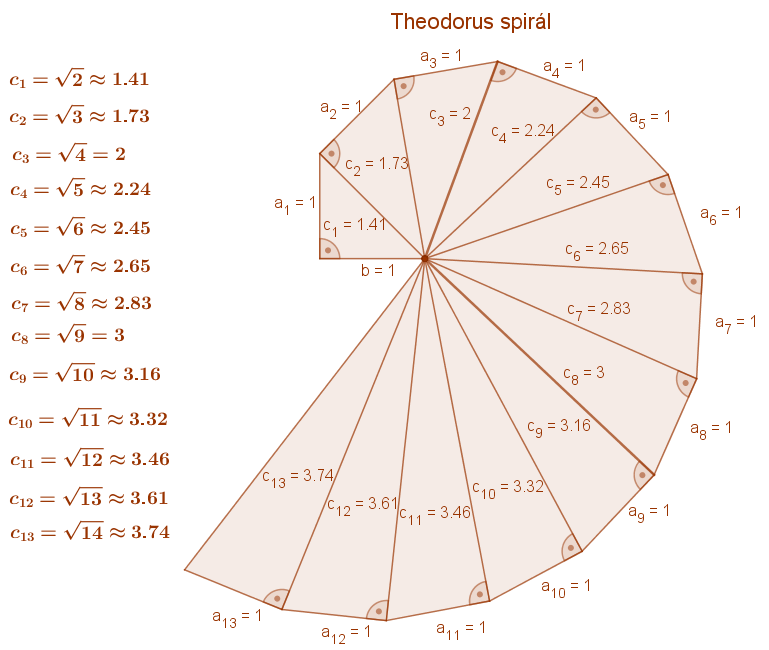
Folytassuk ezt az eljárást! A kapott ADB derékszögű háromszögre emeljünk hasonló módon egy következő derékszögű háromszöget! És így tovább. Így az un. Theodorus spirálhoz jutunk. Itt az egyes háromszögek átfogóinak hossza az egyes – 1-nél nagyobb – pozitív egész számok négyzetgyökével egyenlők. Ebben az eljárásban az egész számok négyzetgyökei sorban, egymás után állíthatók elő.
Egy tetszőleges szám négyzetgyökének szerkesztése a magasság tétel segítségével történhet.
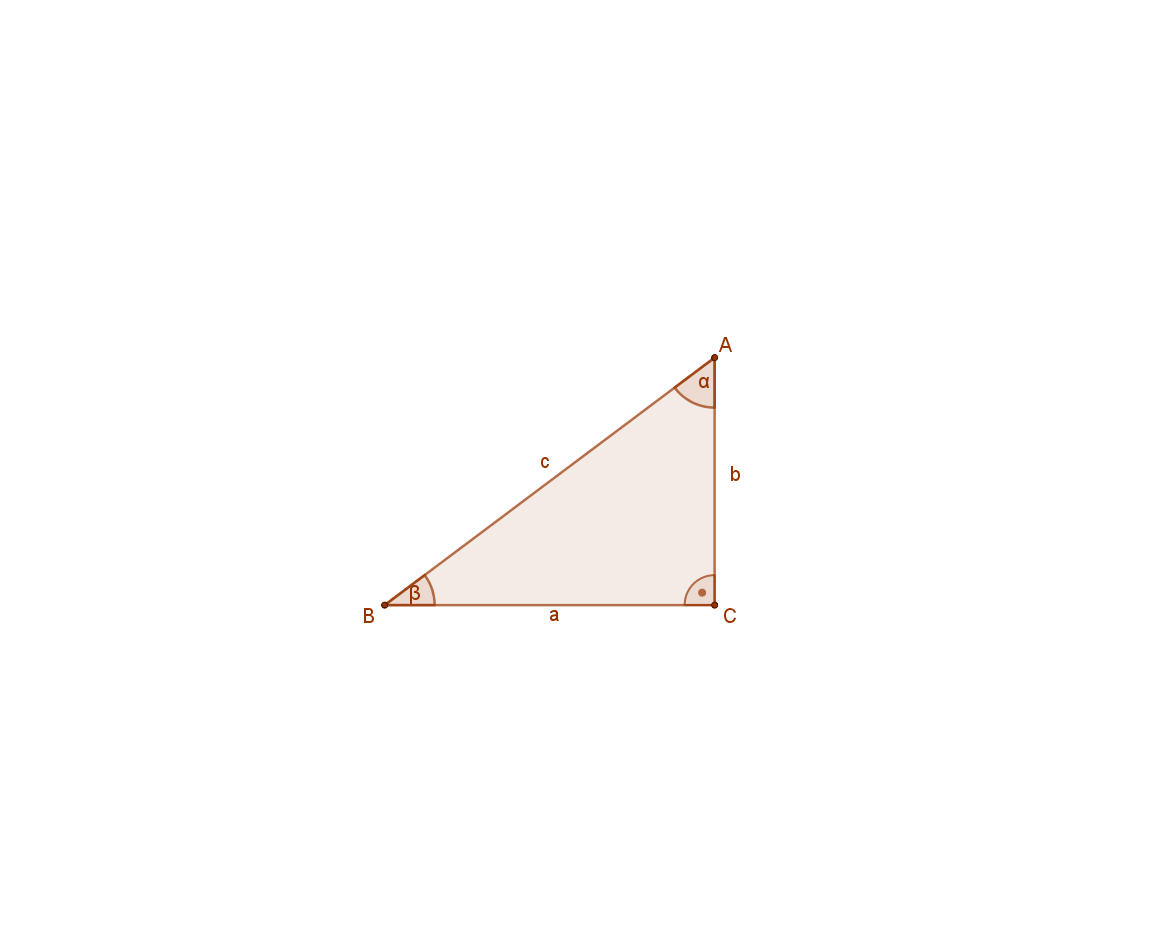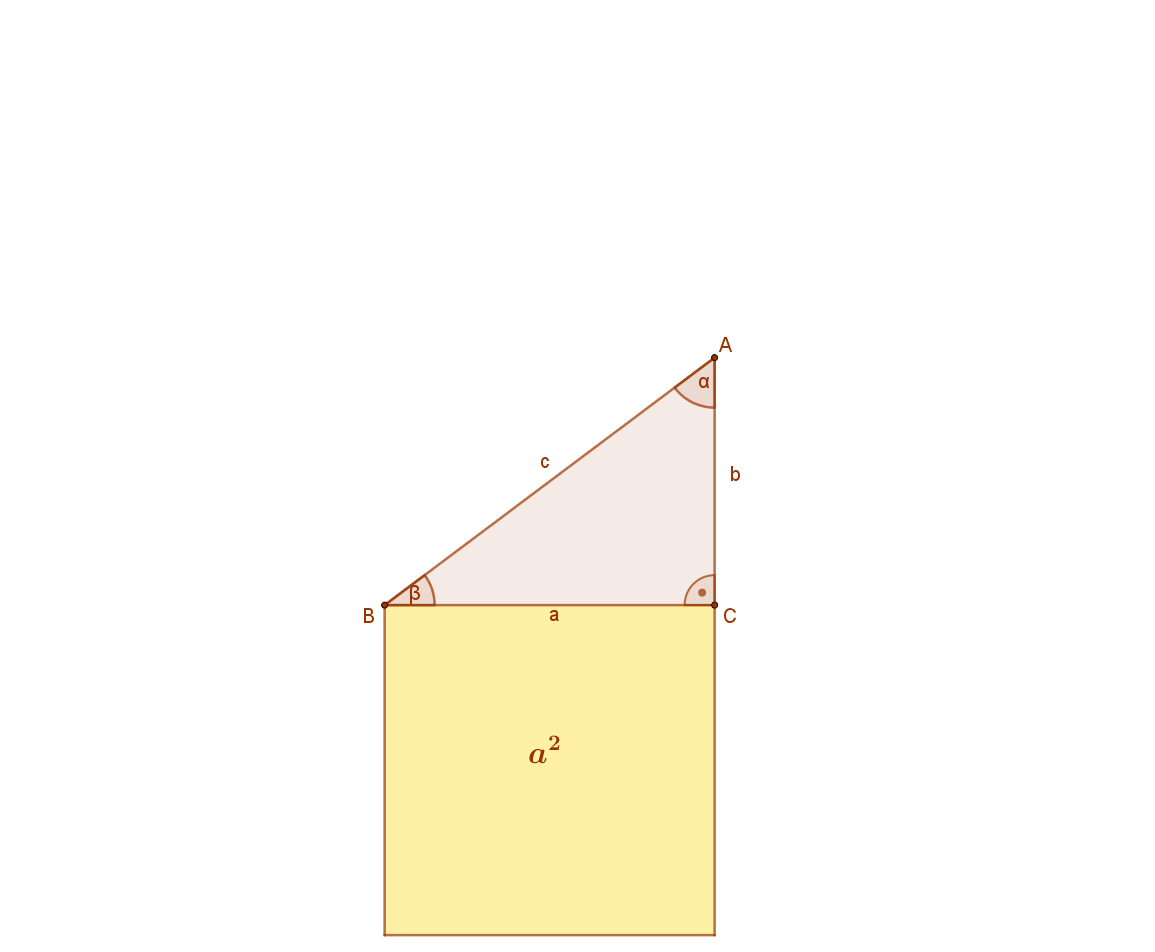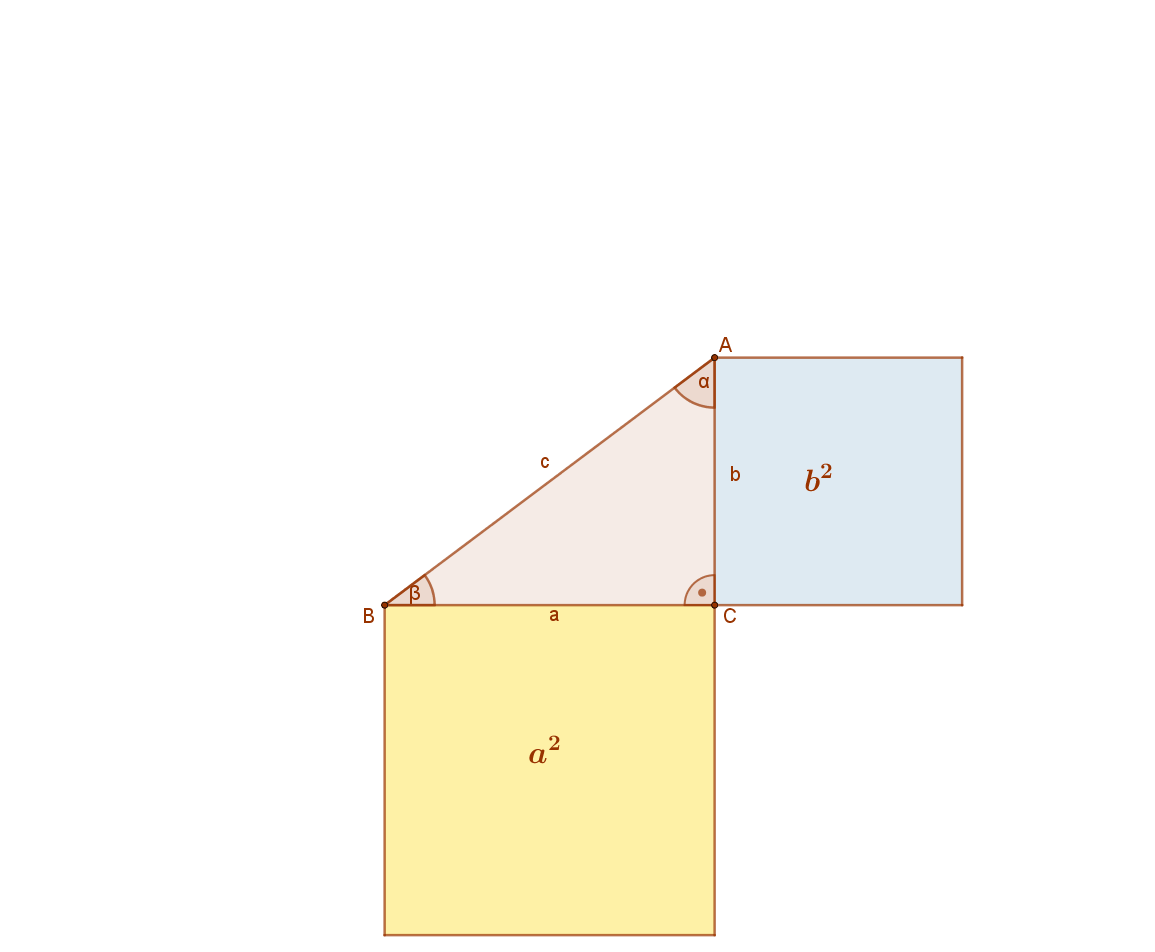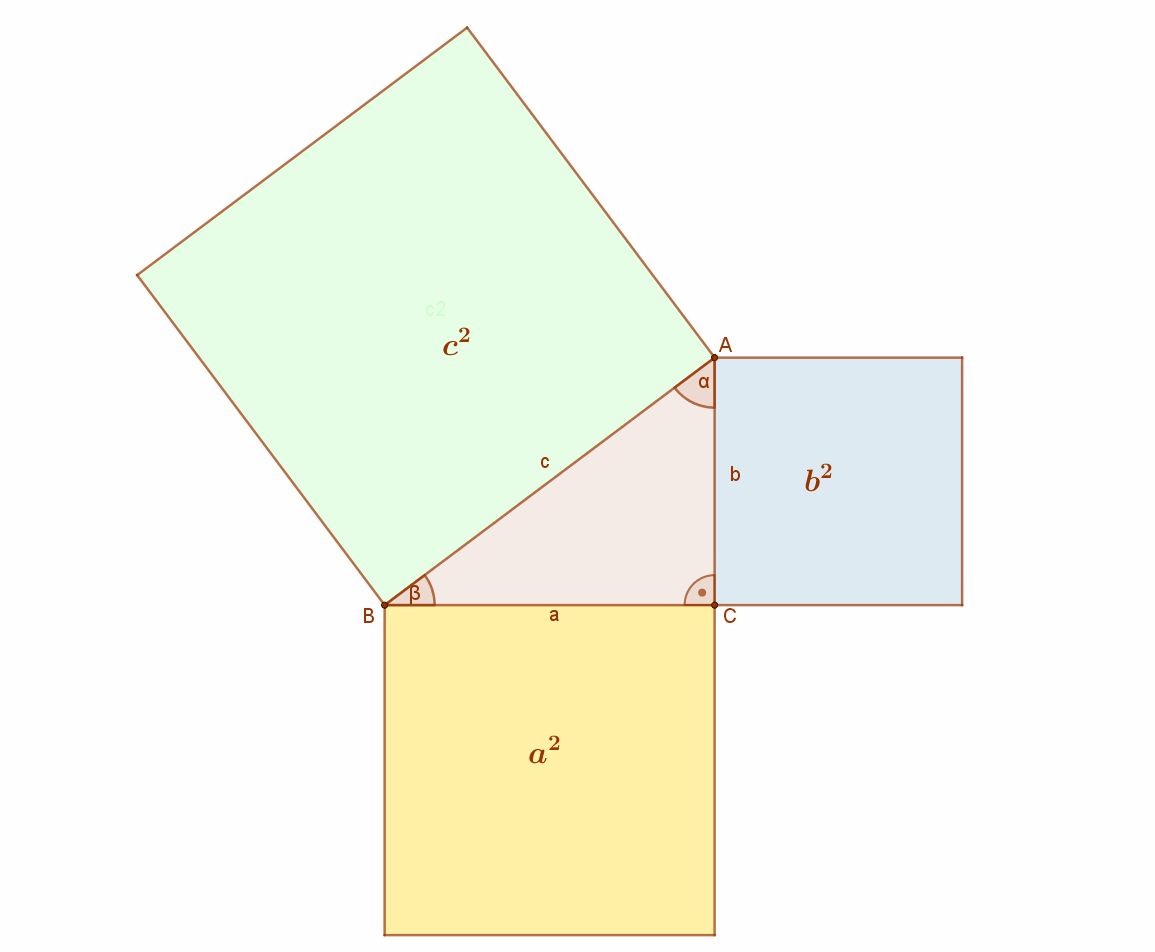
Comments are closed, but trackbacks and pingbacks are open.