Az ellipszis egyenletének meghatározásához induljunk ki az ellipszis definíciójából!
Definíció:
Az ellipszis azoknak a P pontoknak az összessége (mértani helye) a síkban, amelyek a sík két adott pontjától, az F1 és F2 fókuszpontoktól való távolságaik (r1, és r2 vezérsugarak) összege állandó (2a). Ez a távolság nagyobb kell legyen, mint a két fókuszpont (2c) távolsága.
Formulával: ellipszis={P|d(P,F1)+d(P,F2)=r1+r2=állandó=2a>d(F1;F2).
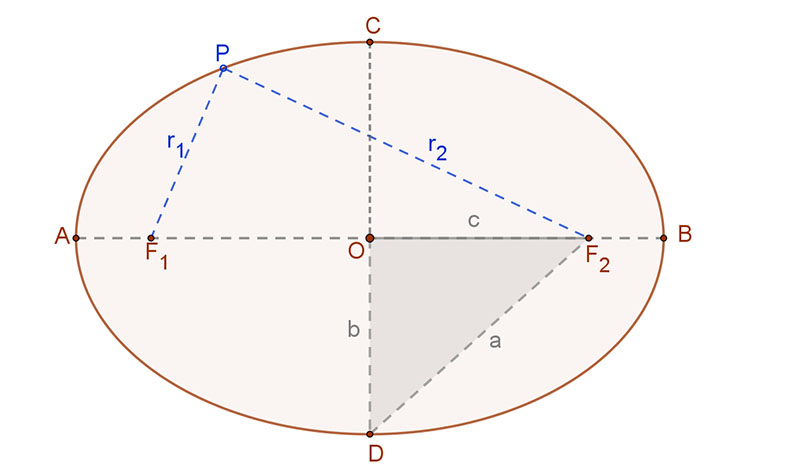A 2a távolság az ellipszis nagytengelye (a mellékelt ábrán az AB távolság, míg erre merőleges az ellipszis 2b hosszúságú kistengelye (CD távolság).
A mellékelt ábrán az ODB derékszögű háromszögben felírva a Pitagorasz tételt: c2=a2-b2.
Helyezzük el az ellipszist a koordináta rendszerben úgy hogy a 2a hosszúságú nagytengelye az „x”, a 2b hosszúságú kistengelye pedig az „y” tengelyre essen. Ekkor az ellipszis középpontja az origó, fókuszpontjainak koordinátái pedig: F1(-c;0) és F2(c;0).
Az ellipszis egyenletéhez fel kell írni az ellipszis tetszőleges P(x;y) pontjának a távolságát a két fókuszponttól. Az ellipszis definíciója szerint ennek a két távolságnak az összege állandó (2a) kell legyen. Ebből kapjuk majd az ellipszis egyenletét.
Állítás:
A fent módon elhelyezett ellipszis P(x;y) pontjaira nézve érvényes középponti egyenlete: \( \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \).
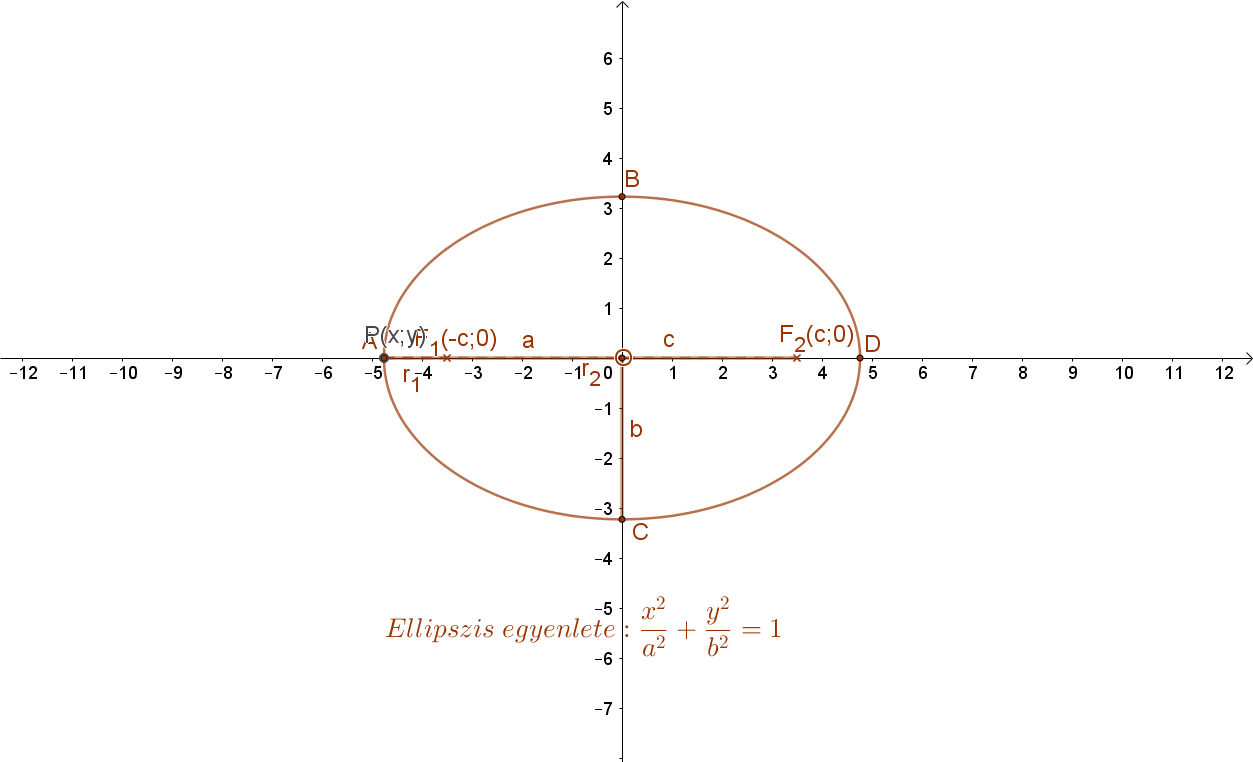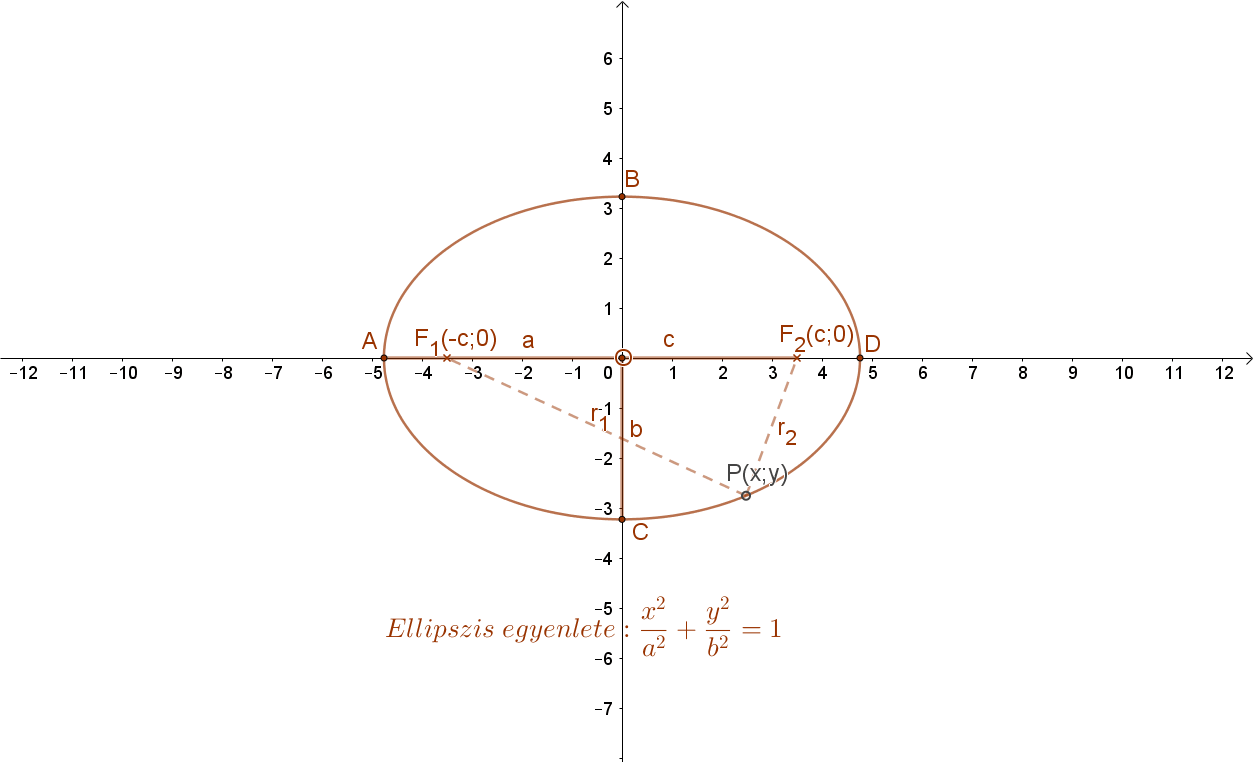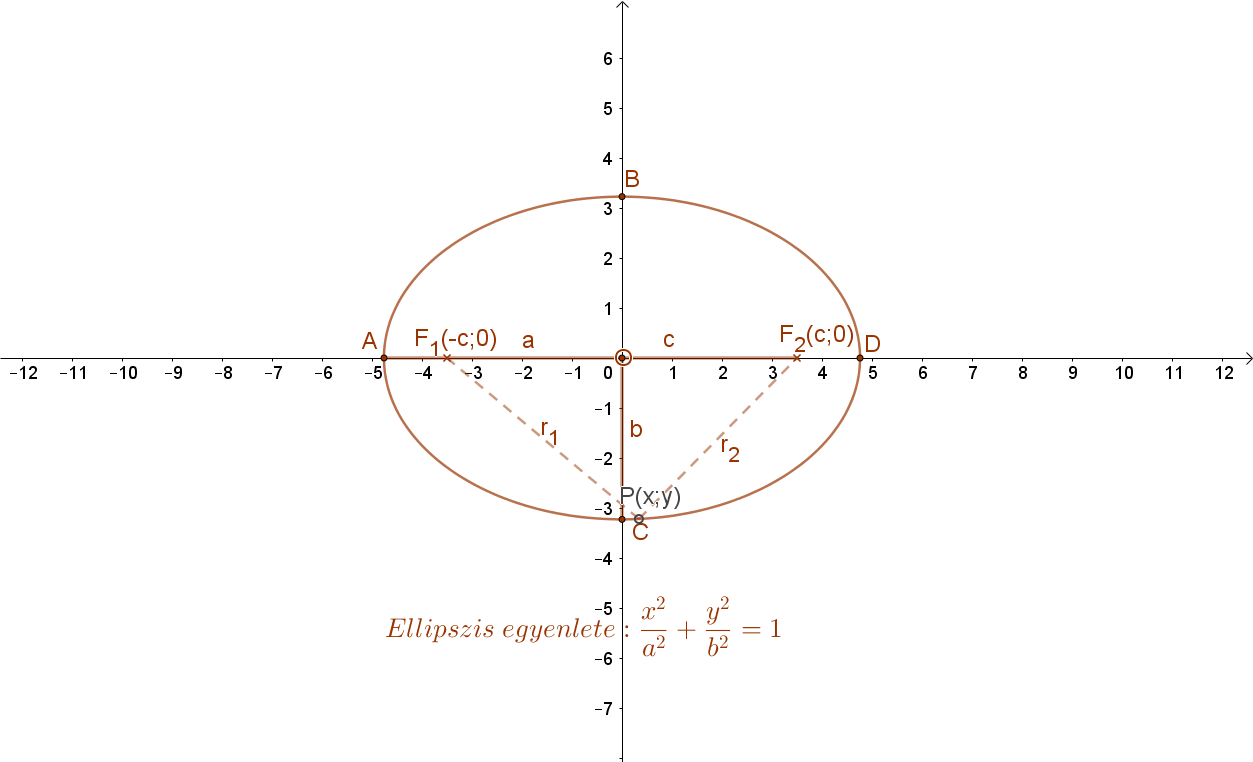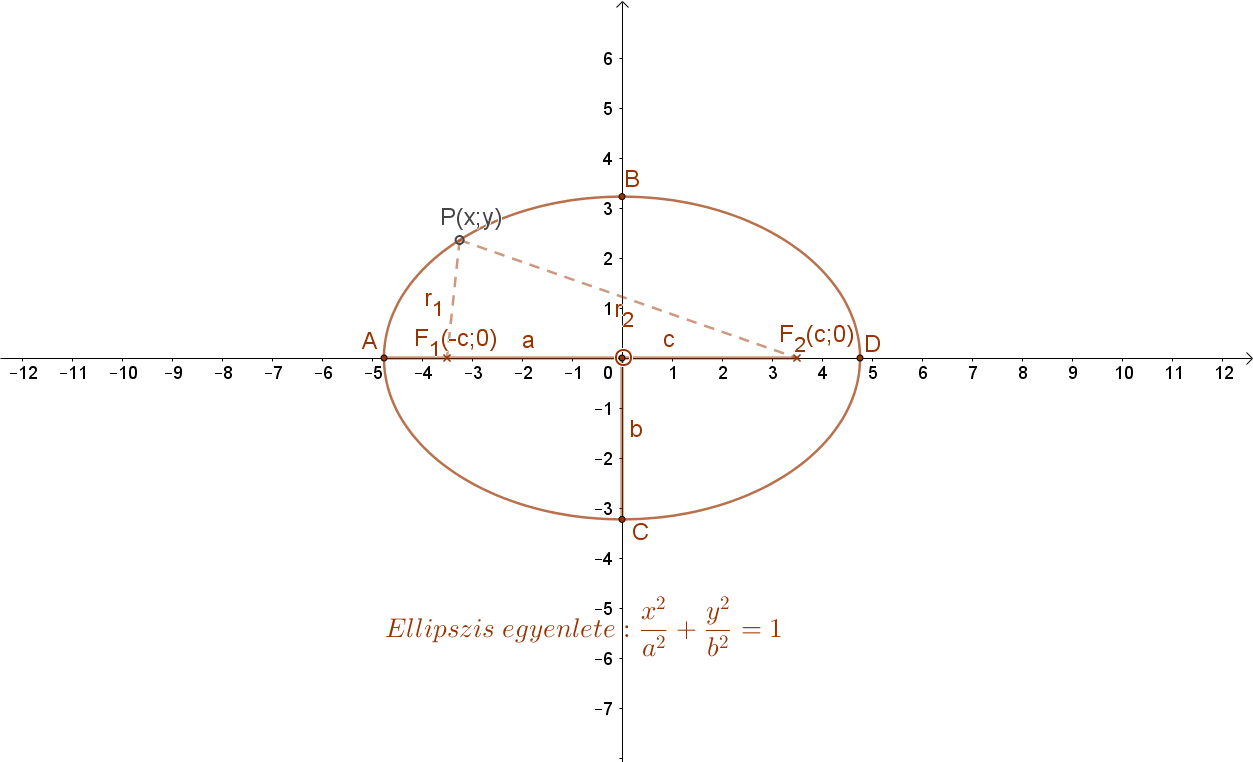
Bizonyítás:
1. P(x;y) pont távolsága az F1(-c;0) fókuszponttól: d(P;F1):
Itt felhasználjuk a két pont távolságára tanult összefüggést:
2. P(x;y) pont távolsága az F2(c;0) fókuszponttól: d(P;F2):
A két távolság összege az ellipszis egyenletét adja:
Természetesen ezt még át kell alakítani, hogy a tétel állításában szereplő formulát megkapjuk!
Csoportosítsunk át!
Emeljük mindkét oldalt négyzetre! 
Vonjunk el mindkét oldalból y2-t!
Bontsuk fel a zárójeleket!
Az egyenlet két oldalán egyező tagokat (x2, c2) vonjuk ki az egyenletből!
Az egyenlet mindkét oldalához adjunk hozzá 2xc-t
!
Csoportosítsunk át és osszuk mindkét oldalt 4-gyel!
Emeljünk négyzetre!
Bontsuk fel a zárójeleket!
Az egyenlet két oldalán egyező tagokat (2a2xc) vonjuk ki az egyenletből! 
Csoportosítsunk át! 
Emeljünk ki a baloldalon x2-t, a jobb oldalon a2-t! 
Felhasználva, hogy a2-c2=b2:
Osszuk az egyenlet mindkét oldalát a2b2-tel! (ami nem lehet nulla):
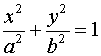
És ezt kellett bizonyítani.
Feladat:
Egy ellipszis egyenlete \( \frac{x^2}{25}+\frac{y^2}{16}=1 \). Milyen hosszúságú vezérsugarak tartoznak azokhoz az ellipszis pontokhoz, amelyeknek akkora az abszcisszájuk, mint a gyújtópontoknak?
(Összefoglaló feladatgyűjtemény 3435. feladat.)
Megoldás:
A megadott egyenletből, az a2=25, és b2=16 értékekből következik, hogy az ellipszis nagytengelye hosszának fele a=5 Így a nagytengely hossza 2a=10, a kistengely hosszának a fele: b=4.
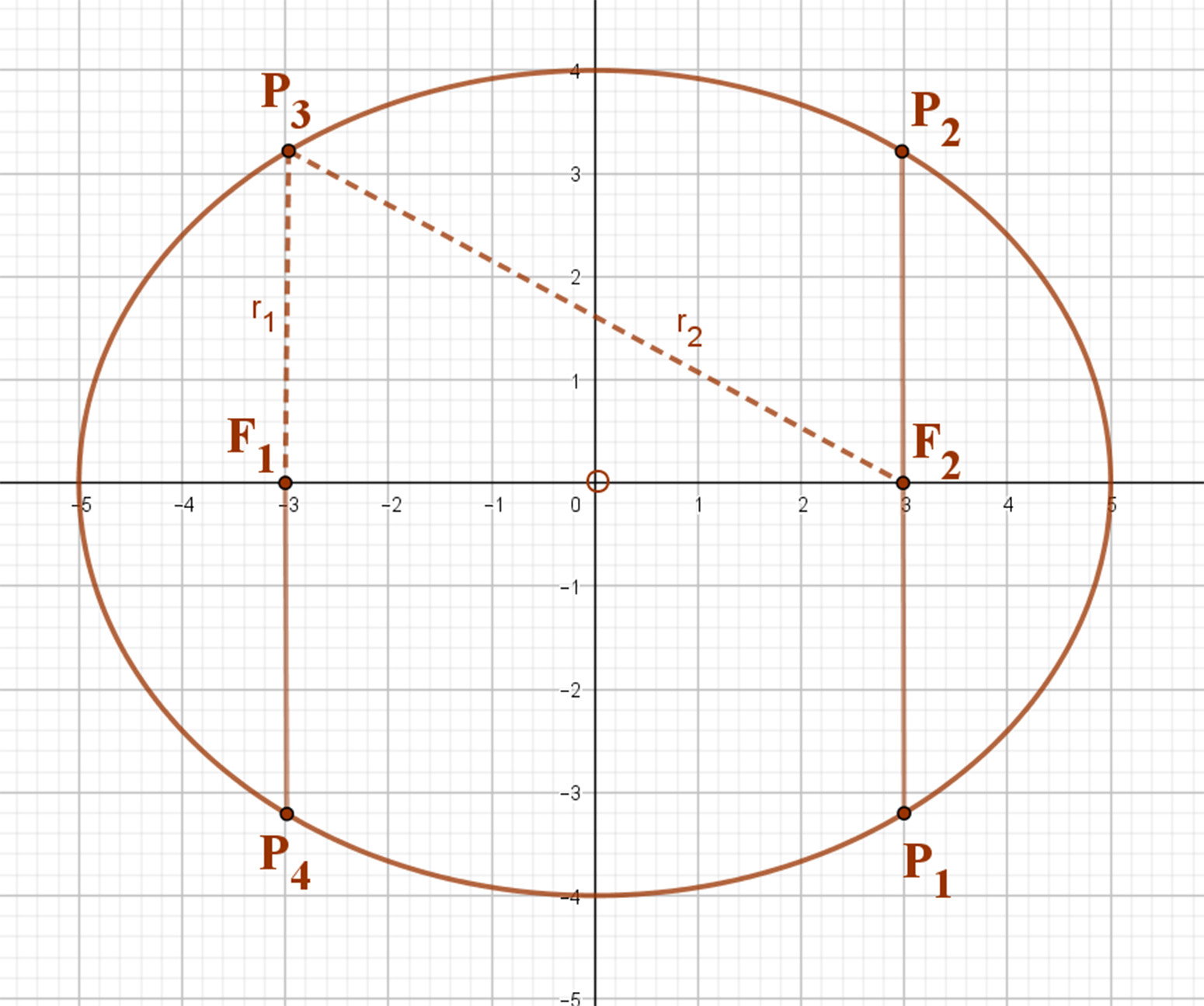Az c2=a2-b2 összefüggés felhasználásával c=3, 2c=6 adódik. Ez tehát azt jelenti, hogy a gyújtópontoknak, az F1 és F2 fókuszpontoknak a koordinátái: F1(-3;0), és F2(3;0).
Ha a fókuszpontokon át párhuzamosokat húzunk az y tengellyel, megkapjuk azokat a pontokat, amelyeknek ugyanakkora az abszcisszájuk, mint a fókuszpontoké (P1, P2, P3, P4).
Ha az ellipszis egyenletébe behelyettesítjük az x helyére a fókuszpontok abszcissza értékét (a 3-t), a kapott egyenletből az y koordináták kiszámíthatók. A \( \frac{3^2}{25}+\frac{y^2}{16}=1 \) egyenletből y1=3,2 és y2=-3,2 adódik.
Az r1 vezérsugár értéke ebben az esetben megegyezik a kapott pontok y koordinátájának abszolút értékével, tehát r1=3,2.
Mivel az ellipszis nagytengelyének hossza egyenlő a két vezérsugár összegével, ezért: r1+r2=10. Ebből következik, hogy a másik vezérsugár értéke ebben az esetben: r2=6,8.
Comments are closed, but trackbacks and pingbacks are open.