Descartes francia matematikus a geometria problémák megoldásához gyakran alkalmazott algebrai módszereket. A szakaszok közötti alapműveleteket úgy igyekezett definiálni, hogy az eredmény ismét szakasz legyen.
Szakaszok összeadása és kivonása természetesen adódott. Azért, hogy két szakasz szorzatát és hányadosát is értelmezni tudja, bevezette az egységszakasz fogalmát és a negyedik arányos szerkesztését, amely a párhuzamos szelők tételére támaszkodik.
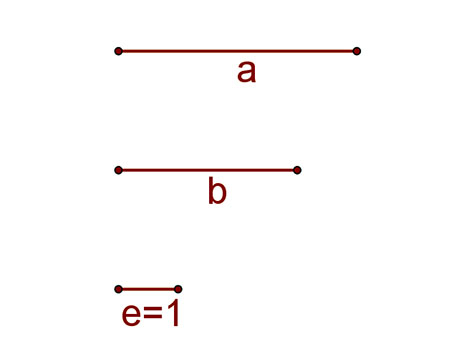
Az egységszakasz definiálásával már el tudta végezni két szakasz szorzatát és hányadosát az alábbi módon:
Legyen adott két „a” és „b” hosszúságú és az „e” egységnyi hosszúságú szakasz.
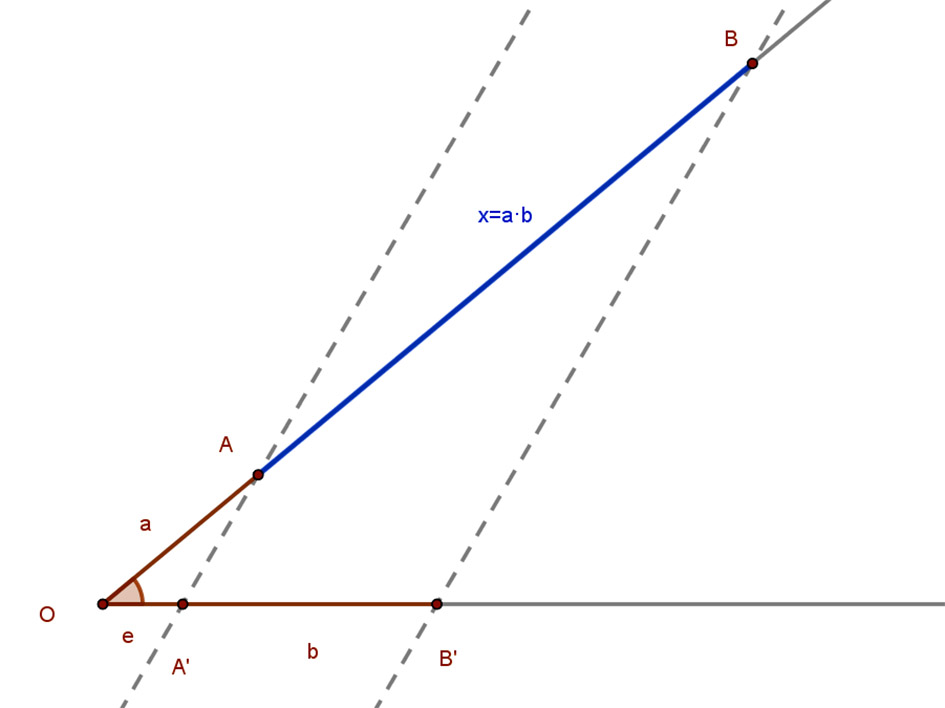
| Az x=a⋅b szakaszt a párhuzamos szelők tételével a következőképpen szerkeszthetjük: Felmérjük egy szög egyik szárára az e=1 egységszakaszt, majd mögéje mérjük a megadott egyik szakaszt (itt a b-t) Majd a szög másik szárára a megadott másik szakaszt (itt az a-t) Párhuzamosokat húzva, megkapjuk a keresett x=a⋅b hosszúságú szakaszt. Hiszen a párhuzamos szelők tétele miatt: e:b=a:x. Ebből az aránypárból x-t kifejezve és e helyére 1-t írva, kapjuk: x=a⋅b. |
|
| Az x=b2 szakaszt a fentiekhez hasonlóan tudjuk megszerkeszteni. Itt az a szakasz helyére is a b szakaszt kell mérni. | 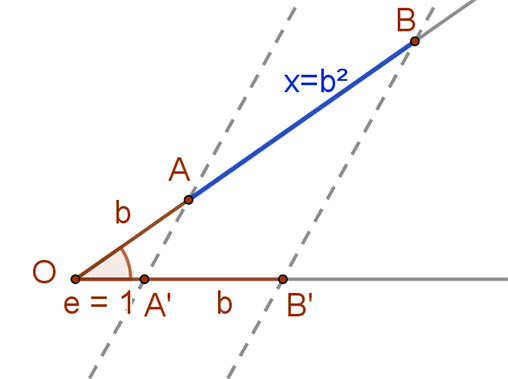 |
| Az x=a/b szakaszt a párhuzamos szelők tételével a következőképpen szerkeszthetjük: | 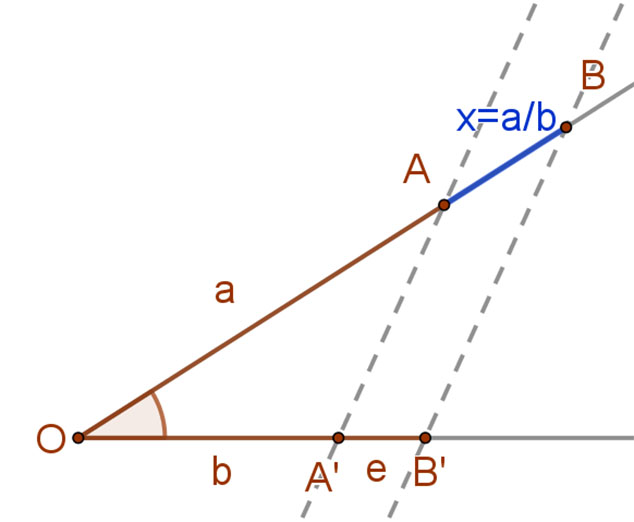 |
| Az x=b/a szakaszt a fentiekhez hasonlóan szerkeszthetjük, csak az a és b szakaszokat kell felcserélni. | 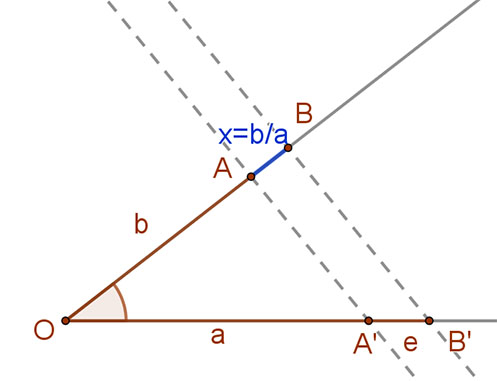 |
| Az x=1/b (reciprok) szakaszt a párhuzamos szelők tételével a következőképpen szerkeszthetjük: | 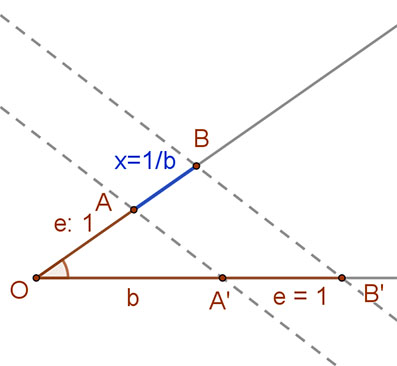 |
Egy „a” szakasz négyzetgyökének a szerkesztéséhez is szükségünk van az e=1 egységszakaszra.
A szerkesztést legkönnyebben a magasság tétel segítségével tudjuk elvégezni.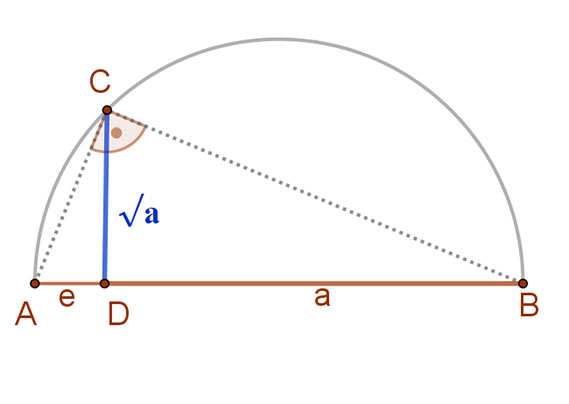
Mérjük egymás mellé az e=1 egységszakaszt és azt a szakaszt (a) amelyiknek a négyzetgyökét meg szeretnénk szerkeszteni.
Az így létrejött 1+a hosszúságú AB szakaszt felezzük el és emeljünk föléje egy Thalész körívet.
Abba a pontba, ahol az egységszakasz és a megadott szakasz találkozik (D) emeljünk az AB átmérőre merőlegest. Ez a merőleges kimetszi a körön a C pontot.
A magasság tétel értelmében az így létrejött DC szakasz hossza=\( \sqrt{a} \)


Comments are closed, but trackbacks and pingbacks are open.