Derékszögű háromszögek magasság tétele

Ezt a tételt a befogó tétellel együtt szokás a derékszögű háromszögekre vonatkozó arányossági tételeknek is nevezni.

Állítás: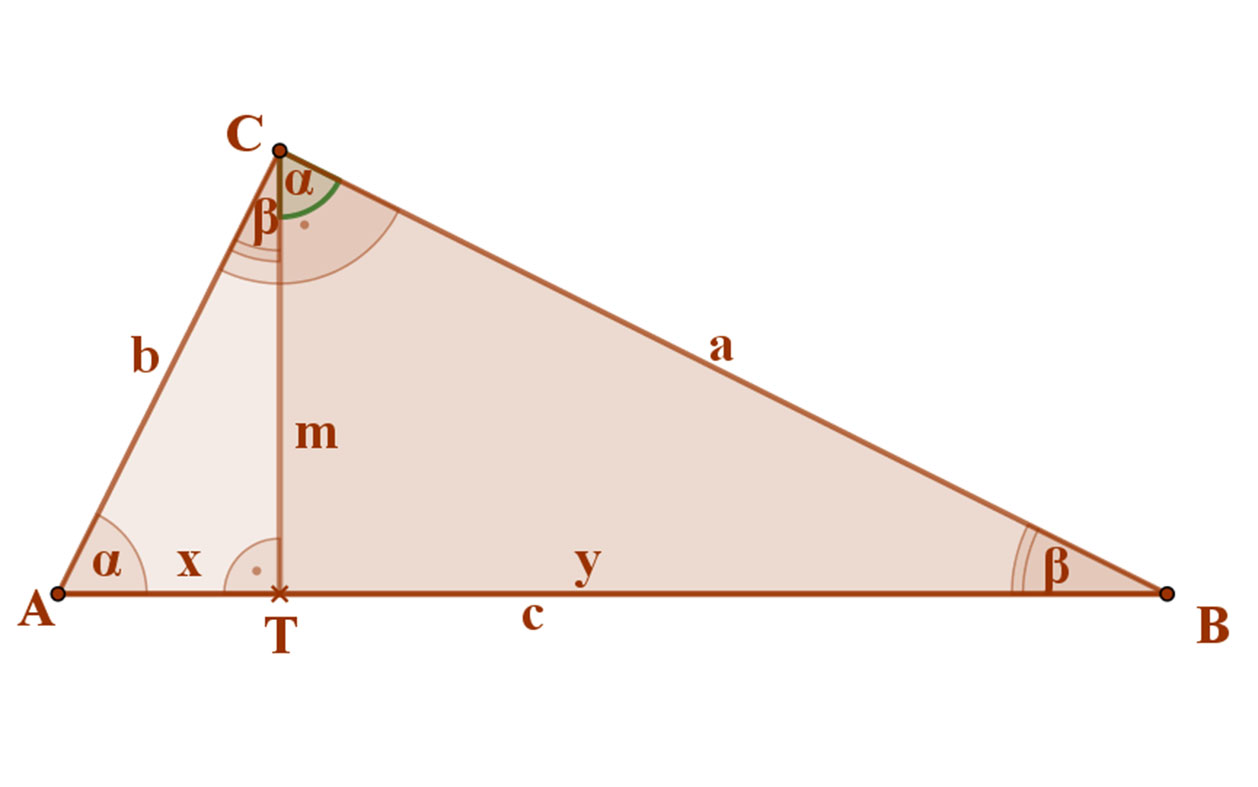

Derékszögű háromszögben az átfogóhoz tartozó magasság mértani közepe az átfogó két szeletének.

A mellékelt ábra betűzése szerint: ​\( m=\sqrt{x·y} \)​.

Bizonyítás:

Az AB átfogóhoz tartozó magasság az ABC háromszöget két derékszögű háromszögre, az ATC és a BTC háromszögekre  bontja.

Ezek háromszögek mindketten hasonlítanak az eredeti ABC háromszöghöz, mivel ezek is derékszögűek, és az egyik hegyes szögük közös. Az ATC háromszögben az α szög, míg a BTC háromszögben a ß szög közös. Emiatt persze a két kisebbik háromszög egymásra is hasonlít.
Tehát: ABCΔ ~ ATCΔ~ BTCΔ.

Mivel az ATCΔ~ BTCΔ , ezért a megfelelő oldalainak aránya egyenlő. Azaz
AT:TC=TC:TB, vagyis x:m=m:y.
Hiszen az m magasság az ATCΔ-ben az α szöggel, míg BTCΔ-ben a β szöggel van szemben.
A fenti aránypárt szorzat alakba írva: m²=x⋅y. Ez azt jelenti, hogy az átfogóhoz tartozó magasság mértani közepe az átfogó két szeletének: ​\( m=\sqrt{x·y} \)​.

Feladat:

Egy derékszögű háromszög átfogója 8 egység, az átfogóhoz tartozó magasság=​\( 2\sqrt{3} \)​ . Mekkorák a háromszög oldalai és szögei?

(Összefoglaló feladatgyűjtemény 1970. feladat.)

Megoldás:

A magasság tétel szerint: m²=xy. Mivel egyrészt a feltétel szerint m=​\( 2\sqrt{3} \), ezért m²=xy=12.
Mivel  y=(8-x), ezért ​\( \left(2·\sqrt{3}\right)^2=x(8-x) \)​ Ezt átalakítva a következő másodfokú egyenletet kapjuk: x²-8x+12.
Ennek gyökei x₁=2 és x₂=6.

Innen már a két befogót Pitagorasz tételével is meghatározhatjuk.
Így b²=x²+m², azaz b²=4+12, azaz b²=16, vagyis b=4. (Mivel a b oldal hosszúság, ezért negatív nem lehet.)
Ugyanígy a²=y²+m², azaz a²=36+12, azaz a²=48, vagyis a=​\( 4\sqrt{3} \).(Mivel az a oldal hosszúság, ezért negatív nem lehet.)

A szögeket a hegyesszögekre vonatkozó szögfüggvényekkel határozzuk meg. ​\( cosα=\frac{x}{b} \)​​, azaz ​\( cosα=\frac{2}{4}=\frac{1}{2} \)​.
Tehát α=60° . Ebből pedig β=30° következik.

Megjegyzés: Mivel a=2⋅m, ezért szögfüggvény alkalmazása nélkül is igazolható, hogy  β=30°.

Hiszen a BCTΔ egy szabályos háromszög fele. Ezt könnyű belátni, ha a „C” csúcsot tükrözzük az AB átfogóra.