A hasonlóság fogalma kapcsolódik az egybevágósági transzformáció, és a középpontos hasonlóság fogalmához.
Definíció:
Hasonlósági transzformációnak olyan geometriai transzformációt nevezünk, amely középpontos hasonlóság és távolságtartó (egybevágósági) transzformáció egymás utáni elvégzésével (szorzatával) jön létre. A transzformáció sorrendje adott kell legyen.
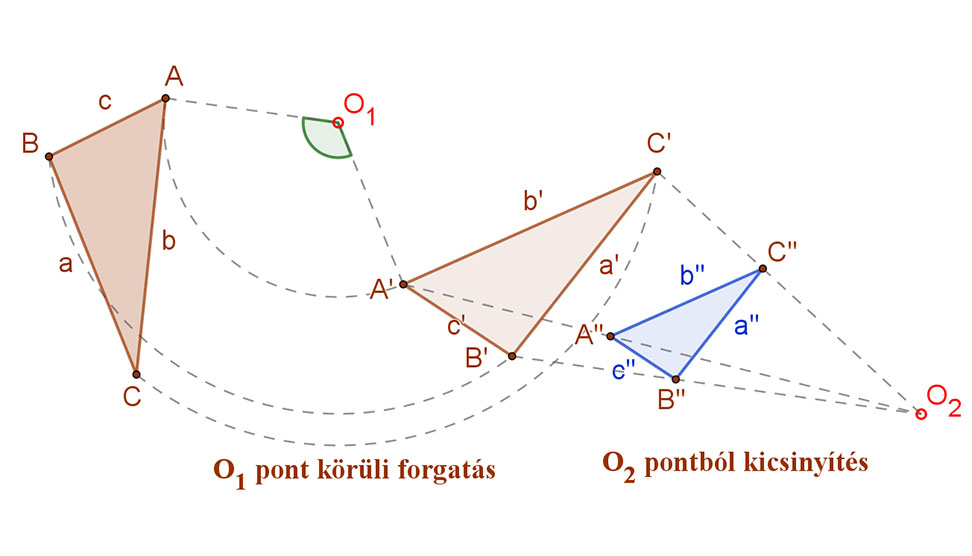
A mellékelt ábrán ABCΔ hasonló az A”B”C”Δ.-höz. Ezt így jelöljük: ABCΔ∼A”B”C”Δ.
Hiszen az ABCΔ egybevágó az ≅A’B’C’Δ- höz, (ABCΔ≅A’B’C’Δ)
mert az ABCΔ-t egy O1 középpontú forgatás viszi át a vele egybevágó A’B’C’Δ-be. Majd az A’B’C’Δ-t egy O2 középpontú középpontos hasonlóság kicsinyíti az A”B”C”Δ- be.
Definíció:
Két alakzatot hasonlónak nevezünk, ha van olyan hasonlósági transzformáció, amellyel az egyik alakzatot a másikba vihetjük át. A hasonlóság jele: ∼.
Két háromszög hasonló, ha:
1. Megfelelő oldalaik hosszainak aránya páronként egyenlő.
2. Két-két oldalhosszuk aránya és az általuk közbezárt szögük nagysága megegyezik.
3. Két-két oldalhosszuk aránya egyenlő és a nagyobb oldallal szembe lévő szögek egyenlők.
4. Ha két-két szögük páronként egyenlő.
Kr. e. 2000 körüli leletekből tudjuk, hogy a babilóniaiak ismerték a háromszögek hasonlóságának a fogalmát.
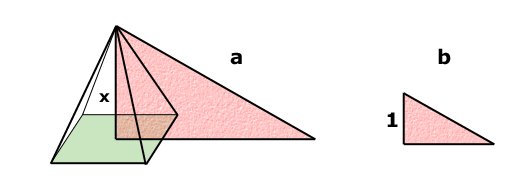 Thalész az egyiptomi piramis magasságának kiszámítását valószínűleg úgy végezte el. hogy egy bot árnyékát mérte meg abban a pillanatban, amikor a bot árnyéka egyenlő volt a bot magasságával. Így ekkor a piramis árnyéka megadta a piramis magasságát. De az is lehetséges, hogy már ismerte és alkalmazni tudta a háromszögek hasonlóságának a fogalmát.
Thalész az egyiptomi piramis magasságának kiszámítását valószínűleg úgy végezte el. hogy egy bot árnyékát mérte meg abban a pillanatban, amikor a bot árnyéka egyenlő volt a bot magasságával. Így ekkor a piramis árnyéka megadta a piramis magasságát. De az is lehetséges, hogy már ismerte és alkalmazni tudta a háromszögek hasonlóságának a fogalmát.
Az ókorban a hasonlóság fogalmát ismerte még Hippokratész is.


Comments are closed, but trackbacks and pingbacks are open.