Thalész

Az első ismert görög matematikus, ezért szokás őt a matematika atyjának nevezni. Életéről keveset lehet tudni. A legismertebb nevéhez fűződő matematikai tétel a Thalész-tétel.

Thalész életéről

A kisázsiai Milétosz városában született. Tekintélyes kereskedő volt, aki beutazta Mezopotámiát és Egyiptomot. Üzleti ügyei mellett a tudományok is érdekelték. Elsősorban a matematika, de csillagászat és a filozófia is. Görögországba ő vitte be a geometriát Egyiptomból. Sokat tanult az egyiptomiaktól, de sok mindent maga fedezett fel. Az ókori matematikában ő az első, aki felteszi a miért kérdést. Az egyiptomiakkal szemben Thalészban döntően új az, hogy bizonyítási igénye volt és igyekezett általánosítani. Mint csillagász i.e. 585.-ben megjósolt egy napfogyatkozást. Még életében, i.e. 582-ben a hét bölcsek közé sorolták. Egyiptomi útja alatt csodálatba ejtette Amazisz fáraót, észrevételeket tett a Nílus árapály-jelenségeivel, és egyetlen bottal meghatározta a piramis magasságát. A görögök között első volt, aki a természet egységének racionális magyarázatára törekedett, ő volt a megindítója a görög matematika fejlődésének. Amikor egy tanítványa megkérdezte tőle, „Mi a legkönnyebb a világon?”, ezt válaszolta: „Másoknak tanácsot adni.” Ismerte őt Pitagorasz. Thalész i.e. 546-ban az olimpiai játékok figyelése közben halt meg.

Thalész munkásságáról

Thalész volt az első, aki matematikai állításait logikai úton bebizonyította. A bizonyításnak deduktív módszerét neki tulajdonítjuk. Több elemi geometriai állítást fogalmazott meg. Lefektette a háromszögek és körök geometriájának alapjait. A szög fogalmának a tisztázása, és a csúcsszögek egyenlőségének a belátása is az ő nevéhez fűződik. Ő mondta ki először, hogy a kört az átmérője két egyenlő részre osztja, valamint azt is, hogy a háromszög szögeinek összege 180°. Thalész állapította meg, hogy az egyenlőszárú háromszögekben a szárakkal szemben egyenlő szögek vannak, és hogy a két háromszög egybevágó, ha egy oldalban és a rajta levő két szögben megegyeznek. Legnevezetesebb azonban a róla elnevezett tétel, amely a derékszögű háromszög és köré írt körének kapcsolatát adja.

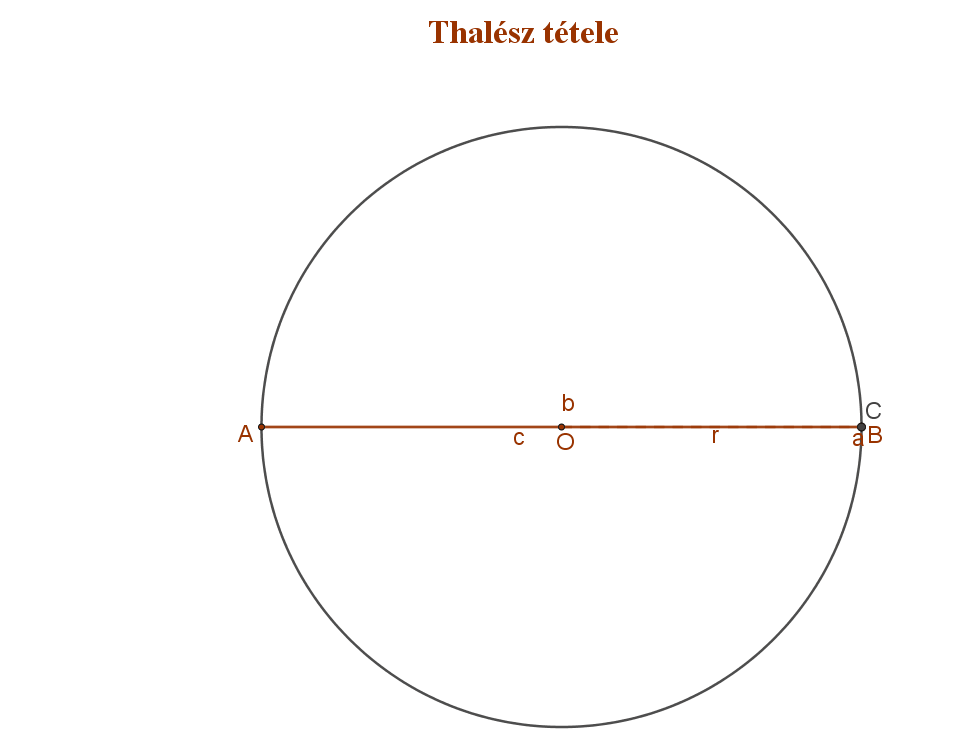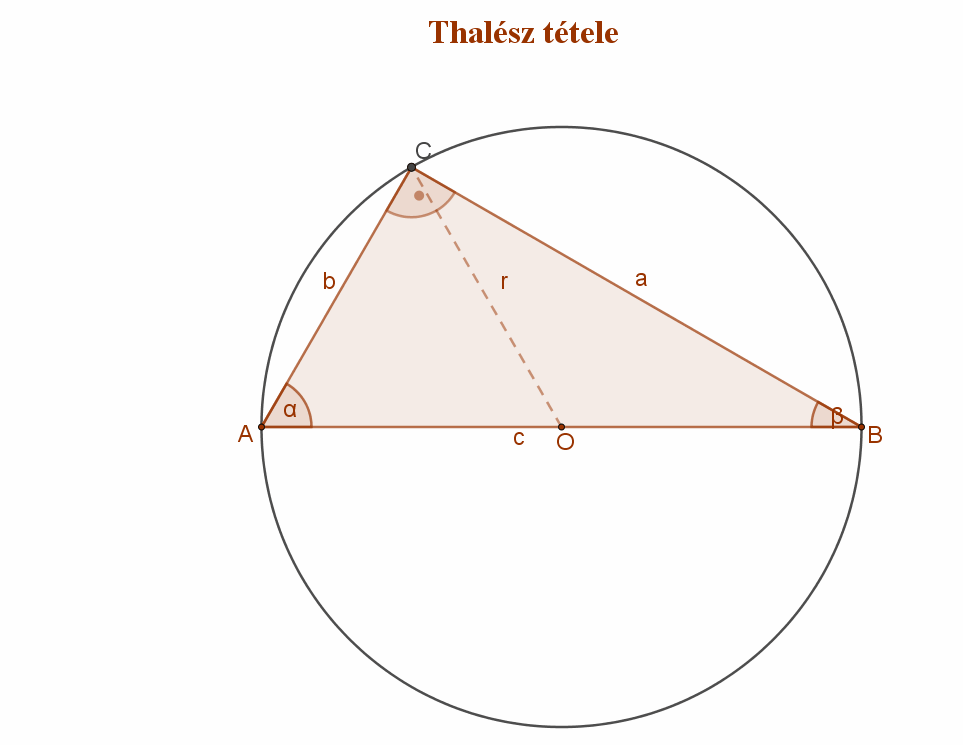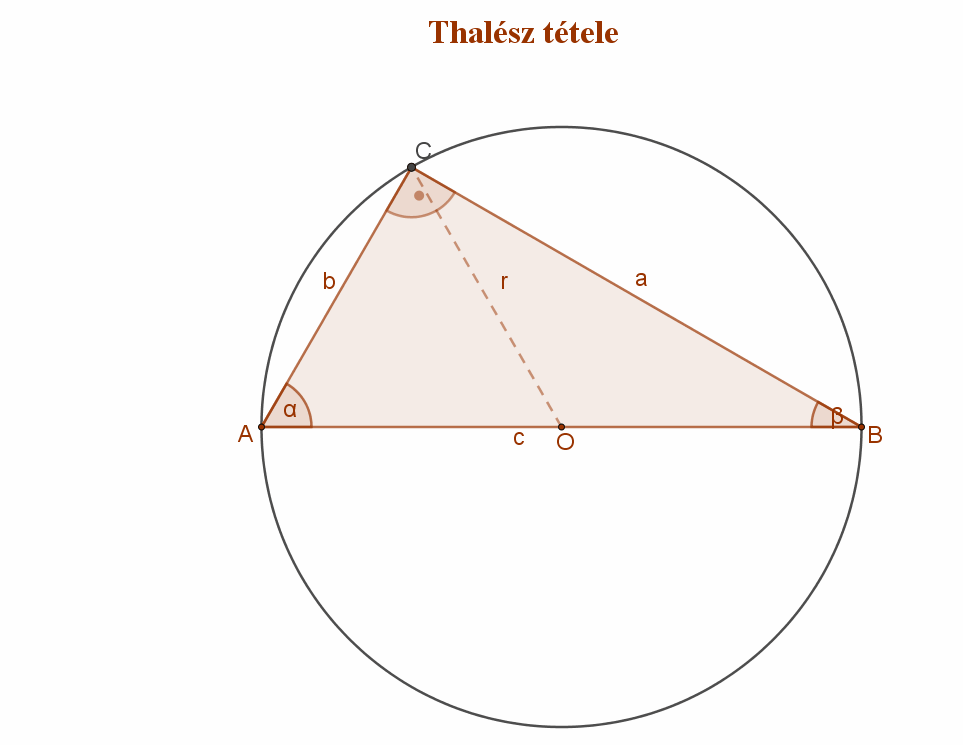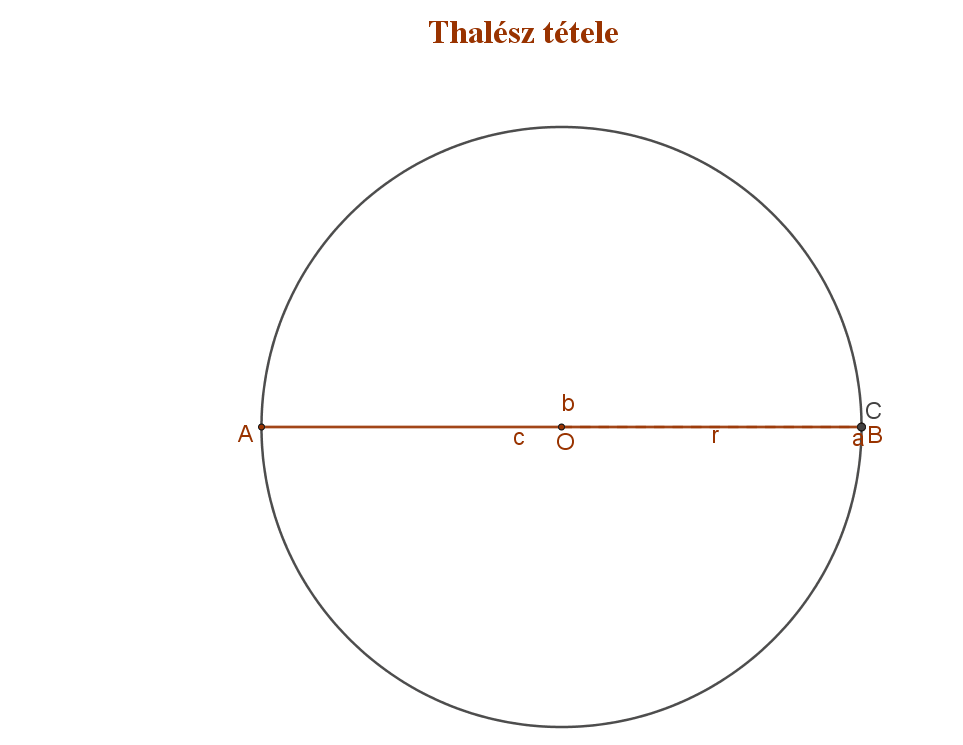
Tétel és bizonyítása: katt a ide.

Thalész az egyiptomi piramis magasságának kiszámítását valószínűleg úgy végezte el. hogy egy bot árnyékát mérte meg abban a pillanatban, amikor a bot árnyéka egyenlő volt a bot magasságával. Így ekkor a piramis árnyéka megadta a piramis magasságát. De az is lehetséges, hogy már ismerte és alkalmazni tudta a háromszögek hasonlóságának elvét.

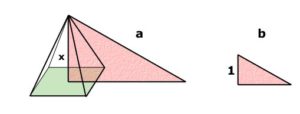
A francia tankönyvek Thalésznek tulajdonítják azt a tételt, miszerint ha egy háromszög egyik oldalával párhuzamos egyenest húzunk, akkor ez a másik két oldal egyenesével az eredeti háromszöghöz hasonló háromszöget alkot.