Példa: Mit jelent ez a közismert KRESZ tábla? A tábla az út emelkedésének a mértékére utal, a függőleges és a vízszintes szakaszok arányát jelenti. A 10%-os lejtőnél 100 méteren 10 méter az emelkedés. A táblán látható kép tehát – természetesen – nem arányos.
Ugyanakkor az emelkedés mértékét a hajlásszög nagyságával is ki lehet fejezni. Ez már trigonometria.
A derékszögű háromszögek oldalainak és szögeinek kapcsolatához induljunk ki a háromszögek hasonlóságából.
Két háromszög hasonló, ha két szöge egyenlő. Hasonló háromszögekben az oldalak aránya egyenlő.
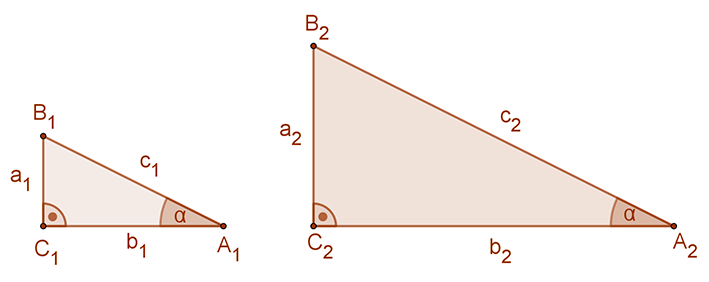Ebből következik, hogy bármely két derékszögű háromszög hasonló, ha egy hegyesszögük egyenlő. Ebben az esetben tehát oldalaik aránya 
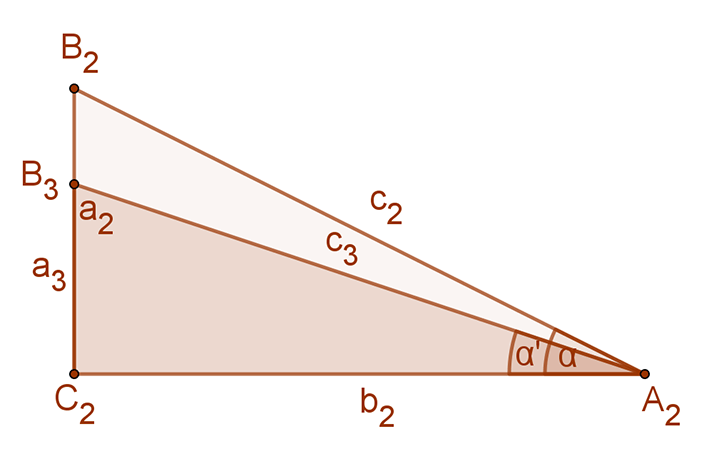egyenlő.
Ha egy derékszögű háromszögben megváltoztatjuk az egyik hegyesszöget, akkor megváltozik az oldalak aránya és fordítva: ha két derékszögű háromszögben az oldalak aránya eltérő, akkor azok nem hasonlóak, hegyesszögeik eltérőek.
Tehát a derékszögű háromszögekben az oldalak aránya jellemző a hegyesszögre, ezért ezeket az arányokat szögfüggvényeknek nevezzük.
Definíciók:
1. Egy derékszögű háromszögben a hegyesszöggel szemközti befogó és az átfogó arányát a szög szinuszának nevezzük.
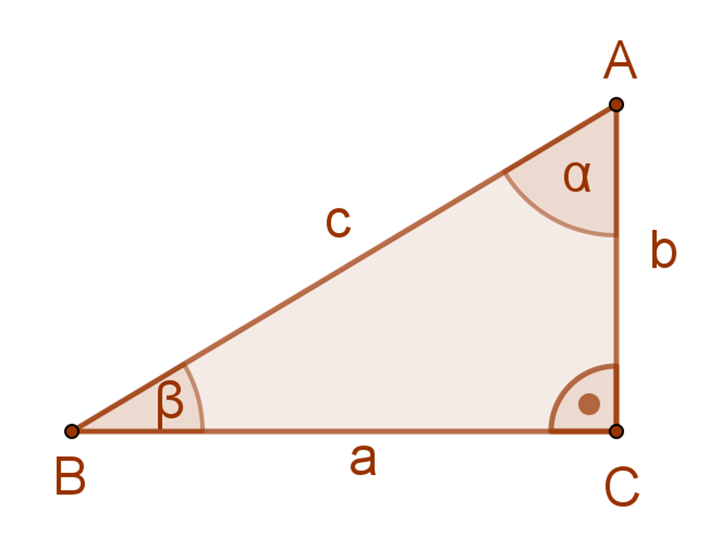A mellékelt ábra jelölései szerint:\( sin(α)=\frac{a}{c} \) és\( sin(β)=\frac{b}{c} \).
2. Egy derékszögű háromszögben a hegyesszög melletti befogó és az átfogó arányát a szög koszinuszának nevezzük.
A mellékelt ábra jelölései szerint: \( cos(α)=\frac{b}{c} \) és \( cos(β)=\frac{a}{c} \).
3. Egy derékszögű háromszögben a hegyesszöggel szemközti befogó és a szög melletti befogó arányát a szög tangensének nevezzük.
A mellékelt ábra jelölései szerint: \( tg(α)=\frac{a}{b} \) és \( tg(β)=\frac{b}{a} \).
4. Egy derékszögű háromszögben a hegyesszög melletti befogó és a szöggel szemközti befogó arányát a szög kotangensének nevezzük.
A mellékelt ábra jelölései szerint: \( ctg(α)=\frac{b}{a} \) és \( ctg(β)=\frac{a}{b} \).
A fenti definíciókból következik, hogy tgα=1/ctgα, valamint ha két hegyesszög egymás pótszöge, azaz egymást 90°-ra egészítik ki, vagyis ha α +β =90°, akkor sinα=cosβ és tgα=ctgβ.
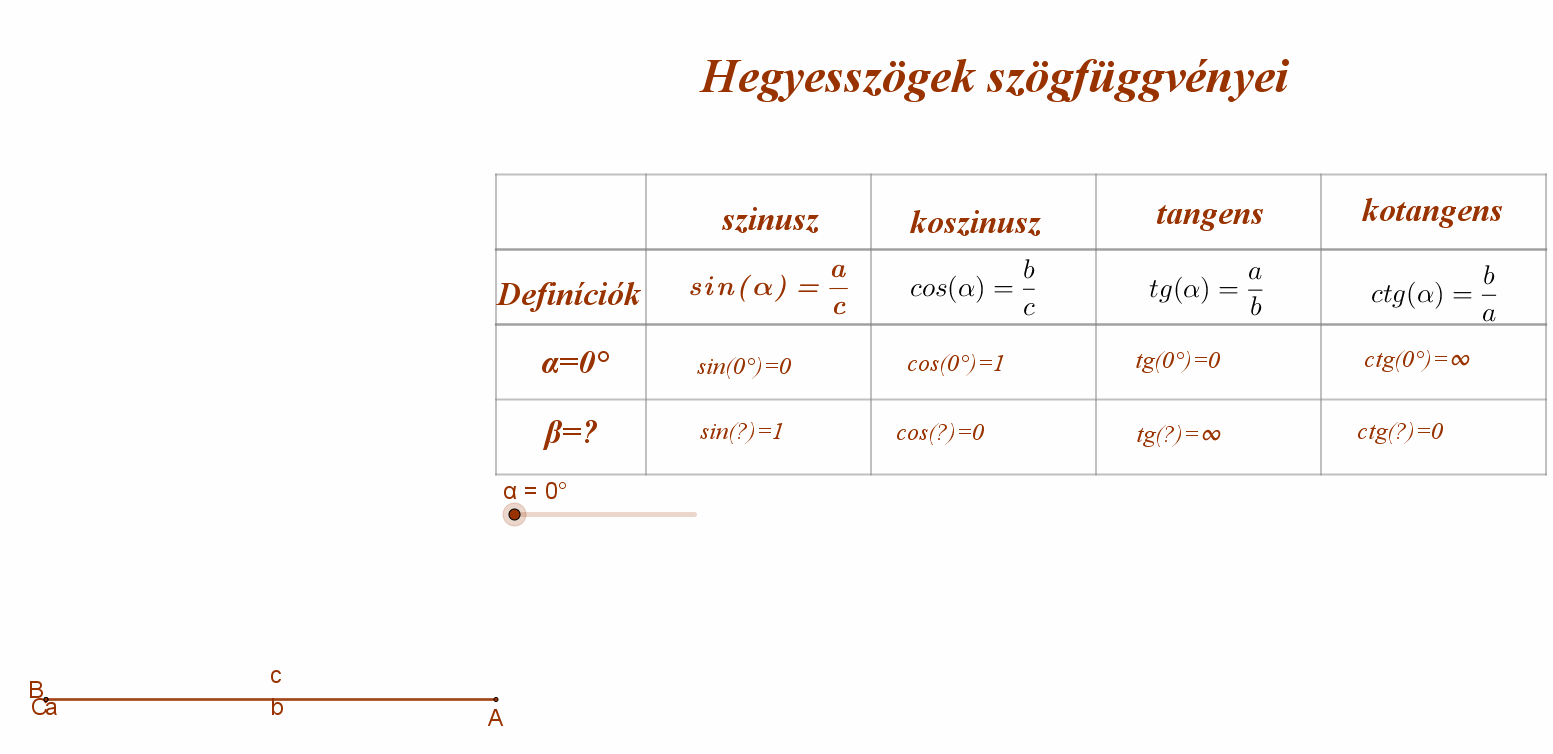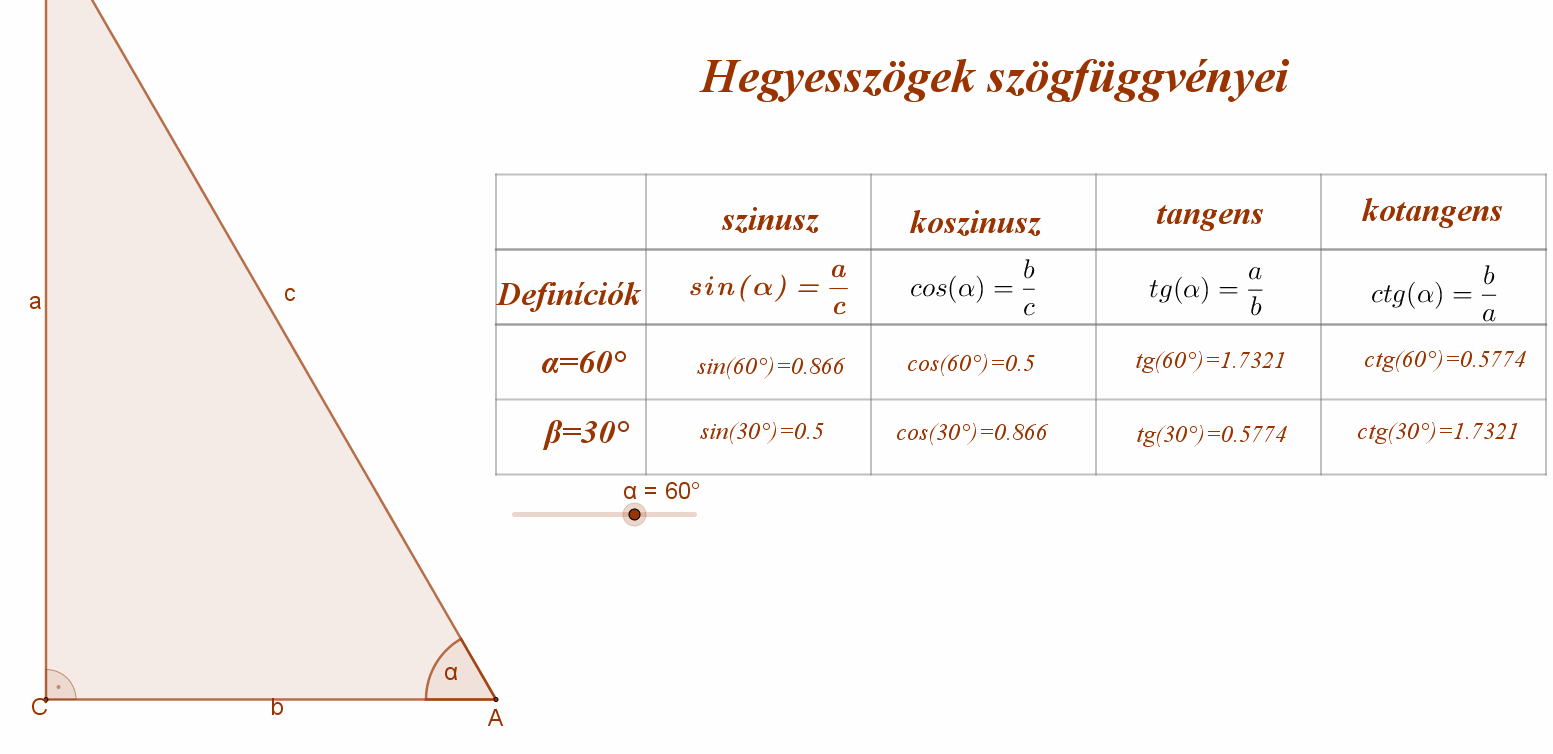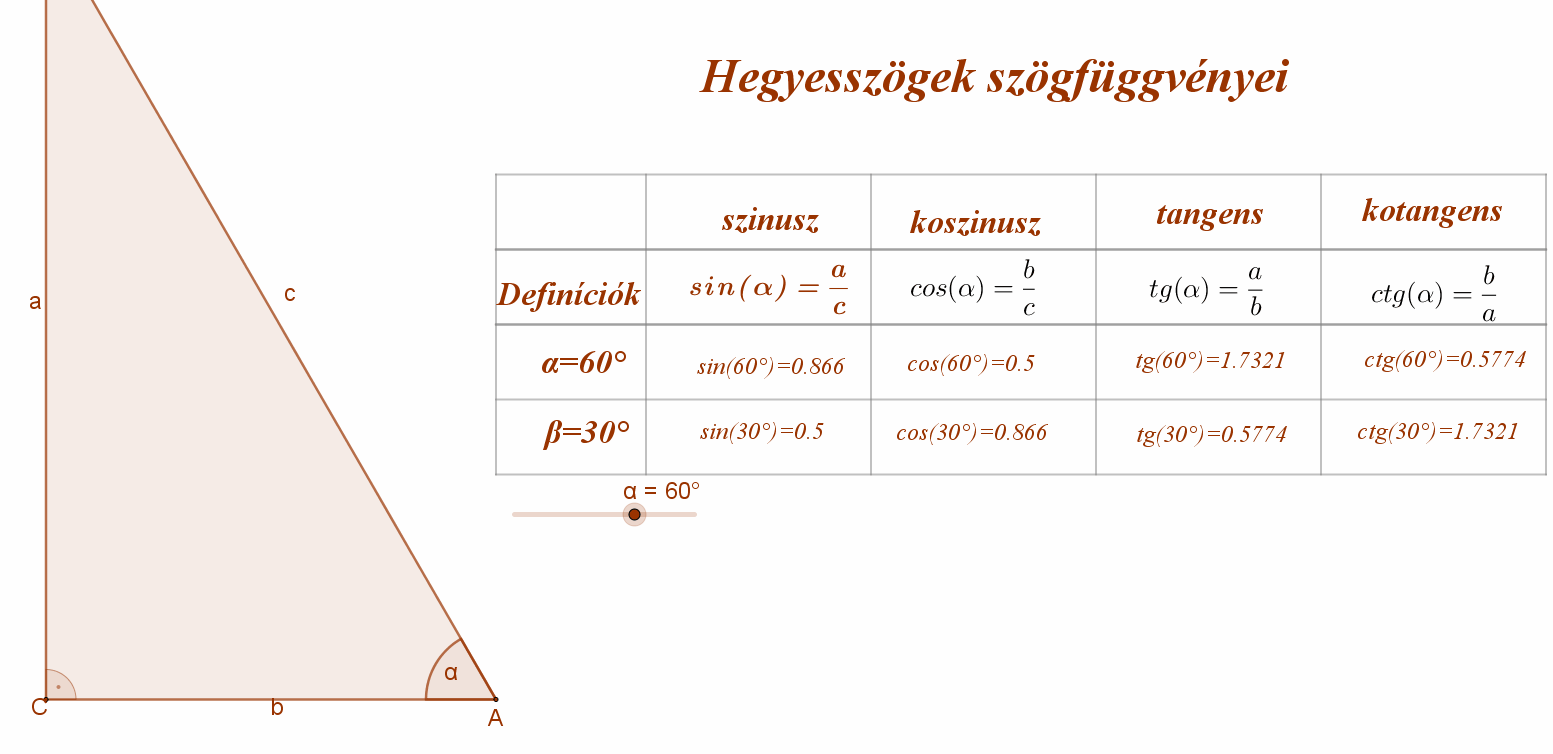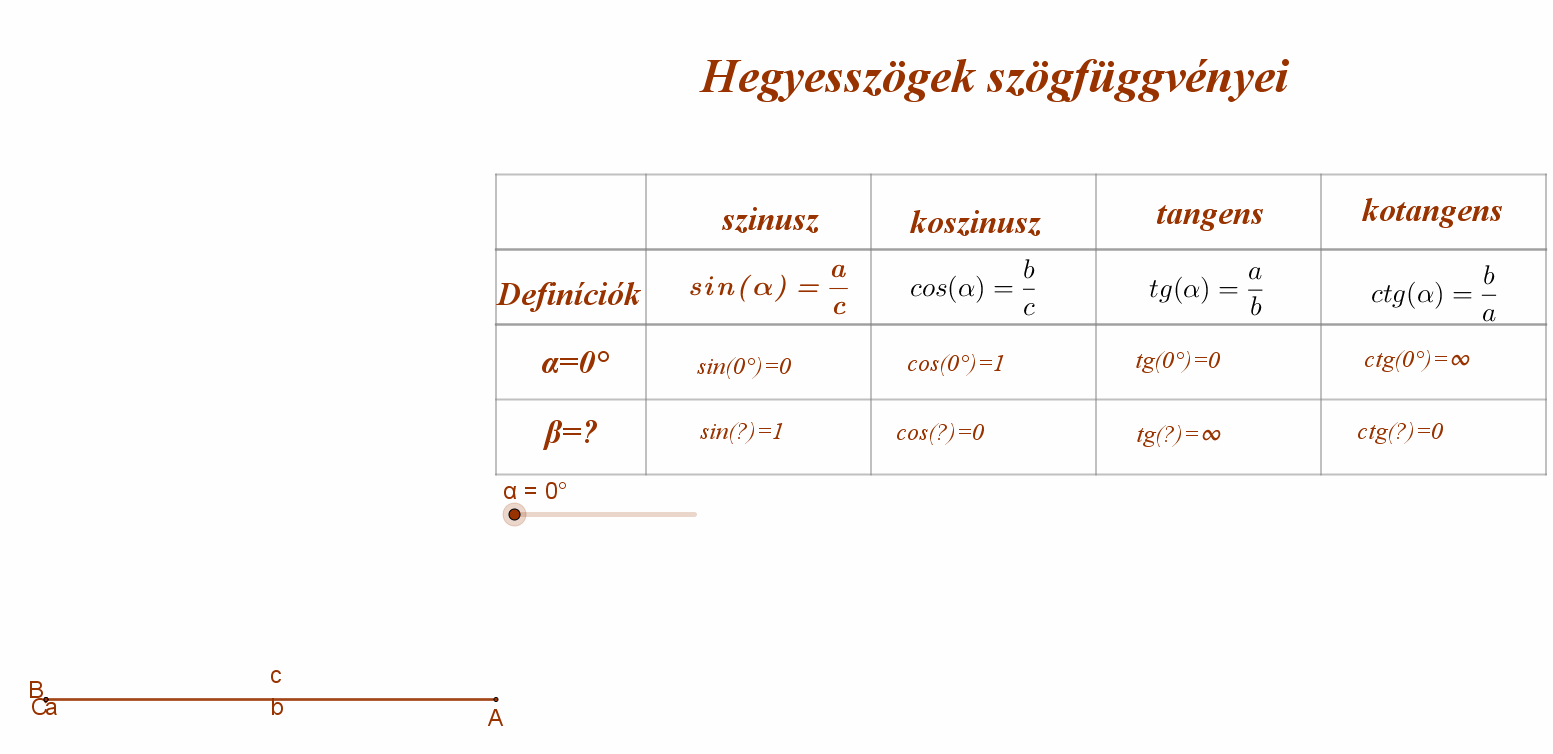Ha egy derékszögű háromszögben az átfogó hossza egységnyi (c=1), akkor a hegyesszöggel szemközti befogó hossza megegyezik a szög szinuszának értékével (sinα=a), és a szög melletti befogó hossza egyenlő a szög koszinuszának értékével (cosα=b).
Ha az egységnyi átfogójú derékszögű háromszögre alkalmazzuk Pitagorasz tételét, akkor a következő összefüggéshez jutunk:
sin2α+cos2α=1.
Ez az összefüggés a szögfüggvények általános értelmezése után is megmarad: ez a trigonometrikus Pitagorasz tétel.
A példa megoldása: Hány fokos a 10%-os lejtő?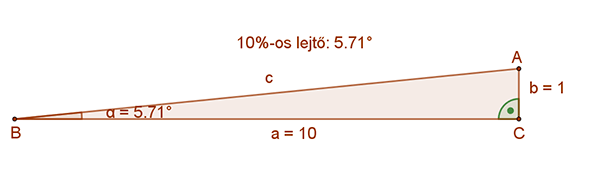
Megoldás: A 10%-os lejtő esetén a derékszögű háromszög két befogójának a hányadosa 10/100=1/10=0.1. Ez azt jelenti, hogy a tangens szögfüggvény segítségével határozható meg a hajlásszög. Vagyis: tg∝=0.1. Így ∝:≈5.71°.
Megjegyzés: A 100%-os lejtő esetén a függőleges és a vízszintes távolság egyenlő. Ez azt jelenti, hogy a 100% lejtő hajlásszöge 45°. Hiszen tg∝=1-ből is ez következik. De a 10 %-os lejtő hajlásszöge nem a 45° 10-ed része, nem 4,5°!
Comments are closed, but trackbacks and pingbacks are open.