Derékszögű háromszögek befogó tétele

Ezt a tételt a magasság tétellel együtt szokás a derékszögű háromszögekre vonatkozó arányossági tételeknek is nevezni.

Állítás:

Derékszögű háromszögben a háromszög befogója mértani közepe az átfogónak és a befogónak az átfogóra eső merőleges vetületének.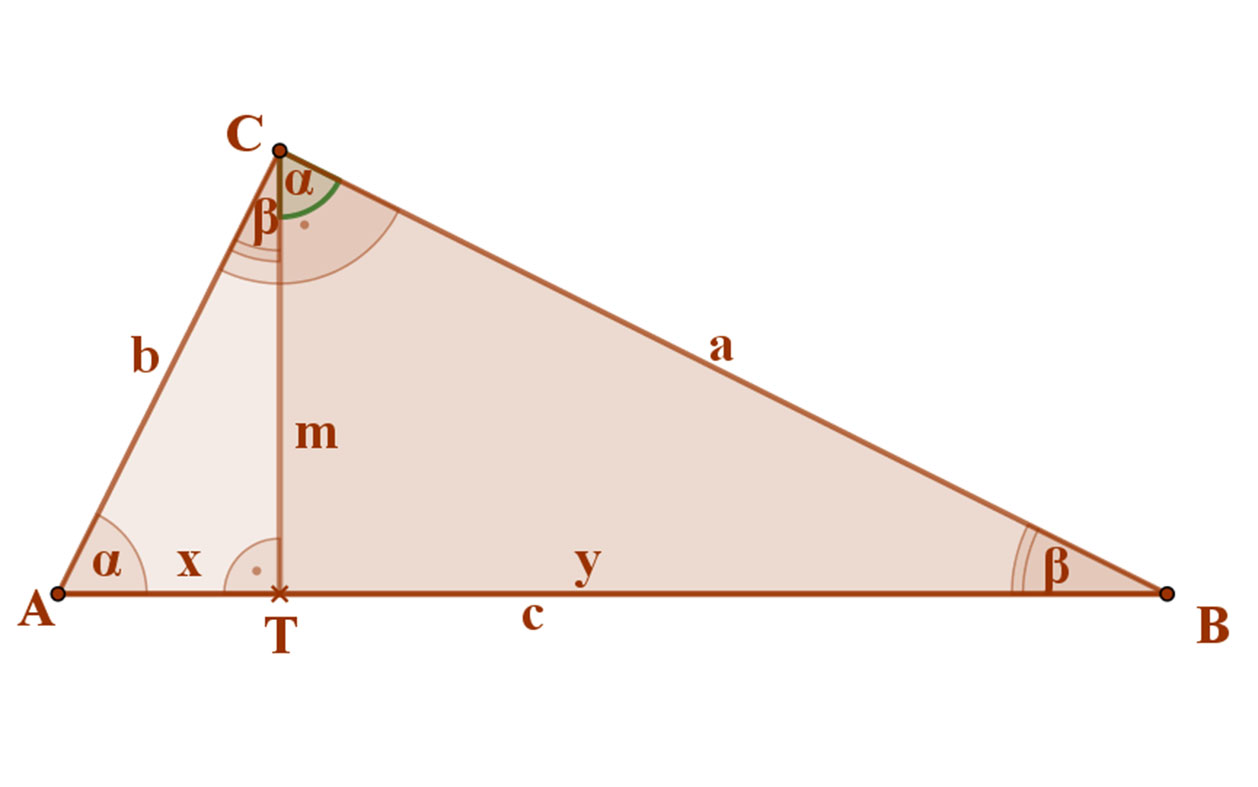

A mellékelt ábra betűzése szerint: ​: ​\( a=\sqrt{c·y} \)​  és  ​\( b=\sqrt{c·x} \)​

Bizonyítás:

Az AB átfogóhoz tartozó magasság az ABC háromszöget két derékszögű háromszögre, az ATC és a BTC háromszögekre  bontja.

Ezek háromszögek mindketten hasonlítanak az eredeti ABC háromszöghöz, mivel ezek is derékszögűek, és az egyik hegyes szögük közös. Az ATC háromszögben az α szög, míg a BTC háromszögben a ß szög közös. Emiatt persze a két kisebbik háromszög egymásra is hasonlít. Tehát: ABCΔ ~ ATCΔ~ BTCΔ.

Az ABC háromszögben az „a” befogónak az átfogóra eső merőleges vetülete a BT szakasz (y), míg a „b” befogónak az átfogóra eső merőleges vetülete az AT szakasz (x).

A bizonyítást most az „a” befogóra vezetjük le.
Mivel az ABCΔ ~ BTCΔ , ezért a megfelelő oldalainak aránya egyenlő. Azaz:  AB:BC=BC:TB, vagyis c:a=a:y.
Hiszen a „c” oldal az ABCΔ-ben átfogó, míg a BTCΔ-ben az „a” oldal az átfogó.
A fenti aránypárt szorzat alakba írva: a²=c⋅y. Ez azt jelenti, hogy az „a” befogó mértani közepe az átfogónak és az átfogóra eső merőleges vetületének: ​\( a=\sqrt{c·y} \)​

A tételt a másik „b” befogóra hasonlóképpen láthatjuk be.

Megjegyzés: A befogó tétel segítségével a Pitagorasz tételének egy újabb bizonyításához jutottunk.

Hiszen: a²=c⋅y. és b²=c⋅x. Így a² + b² =c⋅y+c⋅x.
Itt c-t kiemelve: a² + b² =c⋅(y+x).  De y+x=c miatt a² + b² =c².

Feladat:

A derékszögű háromszög átfogójához magassága az átfogót harmadolja. A háromszög legkisebb oldala 4 cm. Mekkora a többi oldal?

(Összefoglaló feladatgyűjtemény 1949. feladat.)

Megoldás:

 A feltételek szerint a mellékelt ábra jelöléseit használva: AT=x, TB=y=2x, és AC=b=4.
Mivel c=x+y, ezért c=3x.
A befogó tétel szerint b=c*x, tehát
4²=3⋅x⋅x. Azaz 16=3⋅x².

Ebből ​\( x=\frac{4}{\sqrt{3}} \)​. Mivel c=3x, ezért ​\( c=\frac{12}{\sqrt{3}} \)​. A nevezőt gyöktelenítve: ​\( c=\frac{12·\sqrt{3}}3=4·\sqrt{3} \)​.
A hosszabbik „a” befogó már Pitagorasz tételével is számolható. a²=c²-b², azaz: . Ebből ​\( a^{2}=(4·\sqrt{3})^{2}-4^{2}=48-16=32 \)​.
Tehát ​\( a=4\sqrt{2} \)​.