Spirál: síkbeli csavarvonal (csigavonal). Ezek közül az egyik legegyszerűbb az arkhimédeszi spirál.
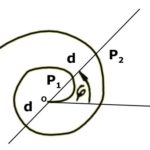
Arkhimédeszi spirál esetén a spirál tetszőleges P pontjának a kezdőponttól való távolsága (r) egyenesen arányos az elfordulás szögével.
Az arkhimédészi spirál polárkoordinátás egyenlete: r=kj, ahol j az elfordulás szöge radiánban, és k egy állandó valós szám.
Az arkhimédészi spirál két egymást követő íve (P1P2) közötti d távolság állandó 2π⋅k, azaz állandó szélességű csigavonal.
Példa:
Ha egy szőnyeget feltekerünk, ilyen arkhimédészi spirált kapunk. A keletkező henger átmérőjének kiszámítása egy számtani sorozat összegének meghatározását jelenti.
Lásd még: https://hu.wikipedia.org/wiki/Arkhim%C3%A9d%C3%A9szi_spir%C3%A1l


Comments are closed, but trackbacks and pingbacks are open.