Szög mérése

Szög fogalma:

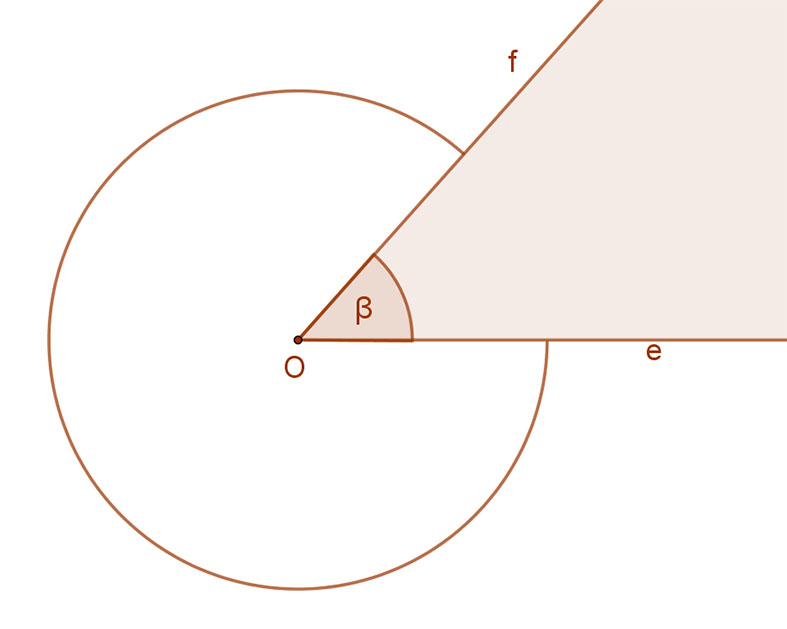
Az egy pontból kiinduló két félegyenes a rájuk illeszkedő síkot két tartományra, két részre bontja. Ezeket a részeket szögtartományoknak nevezzük.

A két félegyenes (e, és f) tehát két szögtartományt, vagy röviden két szöget hoz létre. A két félegyenest a szög szárainak, közös kezdőpontjukat (O) a szög csúcsának nevezzük. A szögeket a görög ABC kis betűivel azonosítjuk, és egy körívvel jelöljük.

Az egy pontból kiinduló két félegyenes a rájuk illeszkedő síkot két tartományra, két részre bontja. Ezeket a részeket szögtartományoknak nevezzük. A két félegyenes (e, és f) tehát két szögtartományt, vagy röviden két szöget hoz létre. A két félegyenest a szög szárainak, közös kezdőpontjukat (O) a szög csúcsának nevezzük. A szögeket a görög ABC kis betűivel azonosítjuk, és egy körívvel jelöljük.

A szög létrejöttét felfoghatjuk úgy is, hogy egy félegyenest végpontja körül elforgatunk. Az így kapott síktartományt, azaz szöget forgásszögnek is mondjuk. Ebben az esetben a forgatás mértékén kívül a forgatás iránya is jellemző a szögre. Megegyezés szerint pozitív forgásiránynak az óramutató járásával ellentétes irányt értjük.

A szögeket megkülönböztetjük nagyságuk szerint.

Eszerint van nullszög, derékszög, hegyesszög, tompaszög,  egyenesszög, homorúszög és teljesszög.

Szög mérése

Szög méréséhez, mint minden méréshez, mértékegységre van szükség.

• •  Az egyik talán legelterjedtebb mértékegység a teljes szög 360-ad része, a fok. (Jele:° )

A fok 60-ad része a szögperc (jele:’), a szögperc 60-ad része a szögmásodperc (jele:”), tehát: 1° =60’=3600″. Ebben a mértékrendszerben jól láthatók 60-as számrendszer nyomai. Ennek megfelelően a teljesszög=360°, az egyenesszög = 180°, a derékszög=90°, a hegyesszög<90° , a ß tompaszögre: 90°<ß<180°, a homorúszög>180°.

• • A szög mérésének másik, talán természetesebb mértékegysége az ívmérték (radián).

 A szög fogalma szorosan kapcsolódik az elfordulás révén a körhöz. Egy adott körben a körív hosszúsága és a szög nagysága között egyenes arányosság van. Nagyobb szöghöz nagyobb ívhossz, kisebb szöghöz kisebb ívhossz tartozik. Ez ad lehetőséget az ívmérték fogalmának megalkotásához.

Definíció:

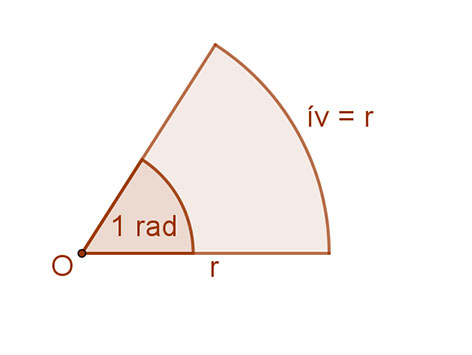Az ívmérték egysége az a szög, amelyhez mint középponti szöghöz tartozó körív hossza egyenlő a kör sugarával. Neve: 1 radián.

A szög ívmértéke tehát egy arányszám, az adott körben az ív és a sugár hosszának az aránya: ​\( \hat{ω} \)=​\( \frac{i}{r} \)​

Mivel a szög (az elfordulás) mértéke független a kör sugarától, ezért tekinthetjük a kör sugarát egységnyinek. Így a teljesszög ívmértéke az egységsugarú kör kerületével egyenlő. Azaz teljes szög=2π radián, az egyenesszög= π radián, stb. Tehát 1 radián a teljes szög 2π -ed része.
Mivel a teljesszög fokban kifejezve 360°, ezért 1 radián fokban kifejezve a 360° -nak 2π -ed része, azaz 1 rad≈57,345°≈57°17’45”.
A két mértékegység közötti átszámításhoz tehát a kulcs: 360°=2π rad, 180°=π rad.

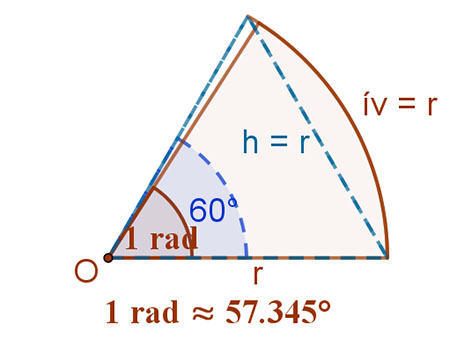A mellékelt ábrán is jól látható, hogy a 60° -os szöghöz a sugárral megegyező hosszúságú húr, míg az 1 radiánhoz a sugárral megegyező hosszúságú ív tartozik.

Az egymáshoz képest speciális (sajátos) helyzetű szögeket szögpároknak mondjuk.