Az egymáshoz képest speciális (sajátos) helyzetű szögeket szögpároknak mondjuk.
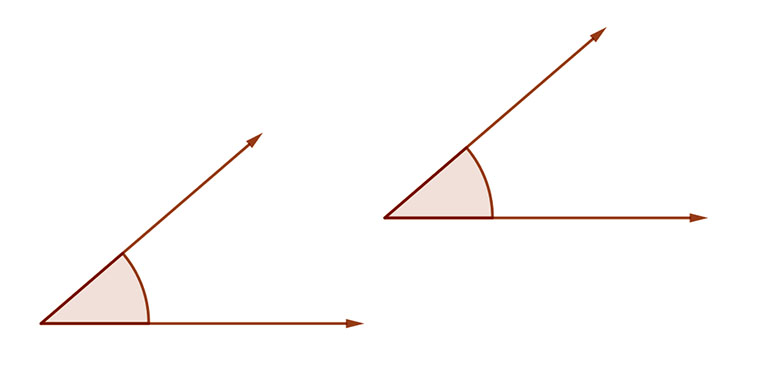 1. Egyállású szögek
1. Egyállású szögek
Ha két szög szárai párhuzamosak és páronként megegyező irányúak, akkor azokat egyállású szögeknek nevezzük.
Az egyállású szögek egyenlők.
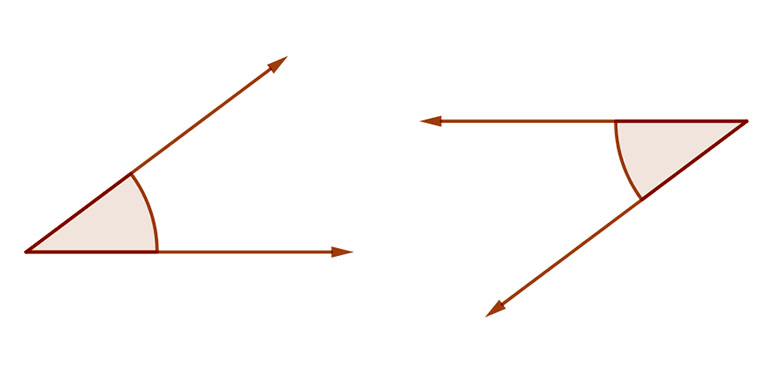 2. Váltó szögek
2. Váltó szögek
Ha két szög szárai párhuzamosak és páronként ellentétes irányúak, akkor azokat váltószögeknek mondjuk.
A váltószögek egyenlők.
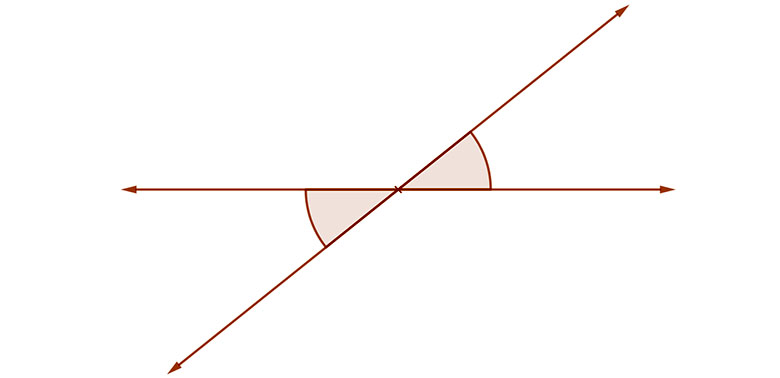 3. Csúcsszögek
3. Csúcsszögek
Azokat a váltószögeket, amelyeknek szárai, és így csúcsai is egy egyenesbe esnek, csúcsszögeknek nevezzük.
Természetesen a csúcsszögek is egyenlők.
4. Kiegészítő szögek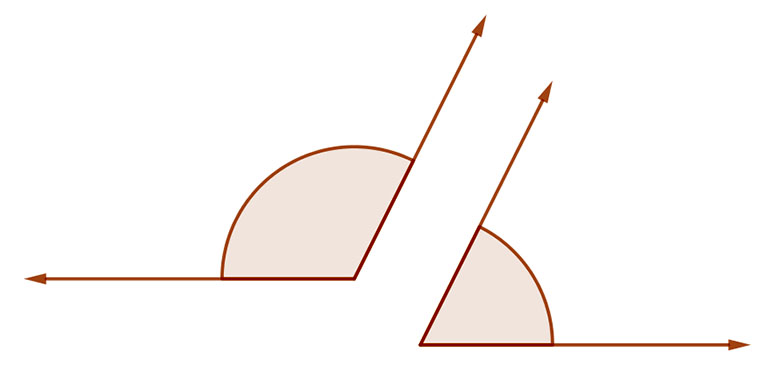
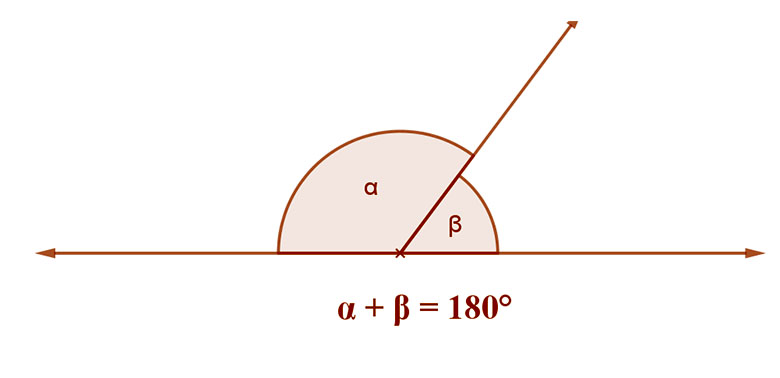
Ha két szög szárai párhuzamosak és az egyik szögszáruk egyező, a másik pedig ellentétes irányú, akkor azokat kiegészítő szögeknek mondjuk.
A kiegészítő szögek összege 180°, azaz egymást 180°-ra egészítik ki.
5. Mellékszögek
Azokat a szögeket, amelyeknek egyik száruk közös, a másik szögszáruk egy egyenesre illeszkedik és ellentétes irányú, mellékszögeknek (társszögeknek) mondjuk.
A mellékszögek is kiegészítő szögek, összegük 180°.
6. Pótszögek
Azokat a szögeket, amelyek összege 90°, pótszögeknek mondjuk.
A derékszögű háromszögek hegyesszögei egymás pótszögei.
7. Merőleges szárú szögek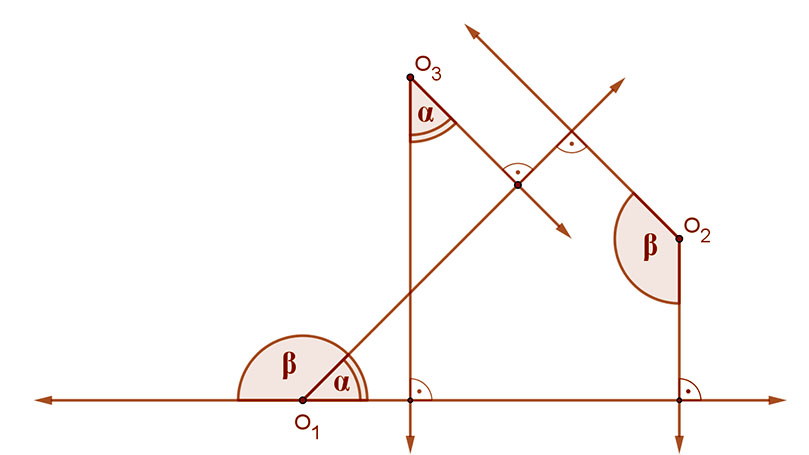
A merőleges szárú konvex szögek szárai páronként merőlegesek egymásra. A merőleges szárú szögek vagy egyenlők, vagy 180°-ra egészítik ki egymást. Egyenlők, ha azonos típusúak azaz ha mindkettő hegyes, vagy mindkettő tompa szögű. Egymást 180°-ra egészítik ki, ha különböző típusúak, azaz egyik hegyes, a másik tompaszög.
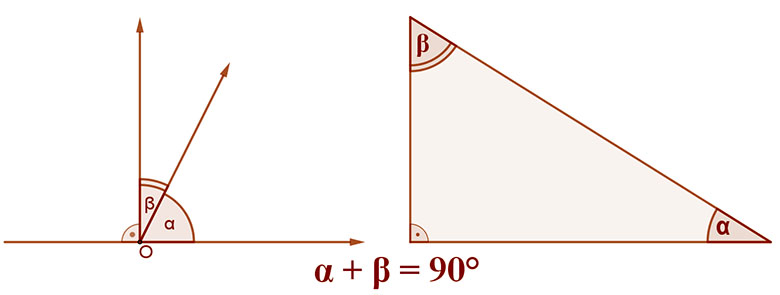


Comments are closed, but trackbacks and pingbacks are open.