Alaki érték, helyi érték
Ma már mindenkinek természetesnek tűnik a tízes számrendszer használata. Ennek lényege, hogy minden egységből 10 darabot egy újabb, nagyobb egységbe foglalunk. 10 darab egyest új egységbe foglalva azt mondjuk, hogy van 1 darab tízes egységünk. 10 darab tízes egység ad 1 darab 100-as egységet. És így tovább. Azt az értéket, amelyik kifejezi, hogy az adott egységből mennyi van, alaki értéknek nevezzük. A tízes számrendszerben 10 darab különböző jel (számjegy) kell az alaki értékek kifejezéséhez: 0-tól 9-ig. Az, hogy ez az alaki érték melyik helyen fordul elő, megmondja, hogy melyik csoportról van szó, ez a helyérték.
Az egyes helyértékek 10 megfelelő hatványával is kifejezhetők: Ezres=103, százas=102, egyesek: 100, tized=10-1 stb. Például: 34 tanuló = 3⋅10 + 4 tanuló. 134,3 azt jelenti, hogy van egy darab 100-as egységem, 3 darab tízes egységem, van még 4 darab egyesem és van 3 darab tizedem valamiből. 2134,3=2⋅103+1⋅102+3⋅101+4⋅100+3⋅10-1.
Tízestől különböző számrendszerek
Ha azonban a csoportosítás nem tízesével történik, akkor egy másik, szintén helyértékes számrendszerhez jutunk. Például legyen a csoportosításunk egysége az 5. Ekkor harmincnégy tanulót ötösével kell csoportosítanunk. Egy öt fős csoport a „tízes”, azaz 5-ös helyérték Mivel 5 darab 5 fős csoport fog létrejönni, szükségünk lesz egy „százas”, azaz 25=52 helyértékre is. Ezen kívül lesz még egy 5 fős csoport és lesznek négyen ezeken kívül. Harmincnégy tanulóból tehát 1 darab 25-ös, 1 darab 5-ös csoport és még négy tanuló: 1⋅52+1⋅51+4⋅50=1145 Ilyenkor a számrendszer alapszámát az alsó indexben jelöljük. Természetesen ebben a számrendszerben csak 5 darab alaki értékre van szükség: 0-tól 4-ig.
Általában, ha „g” jelöli egy számrendszer alapszámát, akkor bármely N szám a következő módon írható fel ebben: N=bk⋅gk+bk-1⋅gk-1+…+b2⋅g2+b⋅g+b0⋅g0+b-1⋅g-1… Itt a bk az egyes alaki értékeknek megfelelő jelek. Minden esetben annyi különböző alaki értékre (írásjelre, számjegyre) van szükség, amennyi a számrendszer alapszáma. Kisebb alapszám eseten kevesebb alaki értékre, de több helyértékre van szükség. tíznél nagyobb alapszámú számrendszer esetén viszont tíznél több alaki érték, több jel kell.
Bináris, azaz kettes számrendszer
A számítástechnikában igen elterjedt a kettes számrendszer használata.
Azért, mert mindössze két darab alaki értékre van szükség, a 0-ra és az 1-re.
Viszont ugyanaz a szám sokkal több helyértéket igényel.
A kettes számrendszerben felírt 1000102 számot tízes számrendszerbe átírva:
1000102=1⋅25+0⋅24+0⋅23+0⋅22+1⋅21+0⋅20= 3410.
Hexadecimális, azaz 16-os alapú számrendszer
Mivel a kettes számrendszerben viszonylag sok helyértékre van szükség, ezért ezek írása a gyakorlatban kényelmetlen, hosszadalmas. Ezért írásban előnyösebb a kettes számrendszerben írt számokat kettő magasabb hatványainak megfelelő számrendszerbe (8-as illetve a 16-os) felírni.
Mivel a 16-os számrendszerben 16 darab alaki értéknek kell lenni, ezért a 0—tó 9 terjedő alaki értékeket betűkkel kellett kiegészíteni.
A 16-os számrendszer alaki értékei tehát.: 0; 1; 2; 3; 4; 5; 6; 7; 8; 9; A; B; C; D; E; F.
A 16-os számrendszerben írt A9B416 számot tízes számrendszerbe átírva:
A9B416= 10∙163+9∙162+11∙161+4∙160=10∙4096+9∙256+11∙16+4=4344410.
Tízes számrendszerben írt számok konvertálása 16-os számrendszerbe
Írjuk át a 10-es számrendszerben felírt 4752710 számot 16-os számrendszerbe!
Megoldás:
Képezzük az adott szám 16-os maradékát: 47527=2970∙16+7. Ez a maradék, a 7-es számjegy kerül a 16-os számrendszerben felírt szám egyes (160) legalsó helyi értékére.
Folytassuk az eljárást a kapott maradékos osztás hányadosával a 2970-nel. 2970=185∙16+10. Ez a most kapott maradék, a 10-nek megfelelő 16-os számrendszernek megfelelő „A” számjegy kerül a 16-os számrendszerben felírt szám második (161) helyiértékére. És így tovább. Az algoritmus (az eljárás), addig folytatódik, amíg a hányados nulla nem lesz.
Az eljárás összefoglalva egy táblázatban:
| Művelet | Hányados (egész) |
Maradék | Hexadecimális számjegy |
Helyi érték |
| 47527:16 | 2970 | 7 | 7 | 160 |
| 2970:16 | 185 | 10 | A | 161 |
| 185:16 | 11 | 9 | 9 | 162 |
| 11:16 | 0 | 11 | B | 163 |
Az eredmény: 4752710=B9A716
Amennyiben a 10-es számrendszerben írt szám nem egész szám, akkor külön kell választani a szám egész és törtrészét.
A törtrész konvertálásnál nem osztunk, hanem szorzunk a számrendszer alapszámával és az a kapott szám egész része lesz balról jobbra haladva a következő számjegy.
Példa: 28,3710 számot tehát a következőképpen írjuk át 16-os számrendszerbe:
Az egész rész (2810) konvertálása a fenti módon történik: 2810=1C16.
A 0,3710 törtrész konvertálását a következő táblázat mutatja:
| Művelet | Hányados (egész) |
Maradék | Hexadecimális számjegy |
Helyi érték |
| 0,37∙16=5,92 | 5 | 0,92 | 5 | 16-1 |
| 0,92∙16=14,72 | 14 | 0,72 | E | 16-2 |
| 0,72∙16=11,52 | 11 | 0,52 | B | 16-3 |
| és így tovább |
Az eredmény tehát: 28,3710≈1C,5EB16.
Ellenőrzés:
1C,5EB16=1∙16+12∙16+5∙16-1+14∙16-2+11∙16-3=28+0,3125+0,0546875+0,002685546=28,369873046…≈28,3710
Megjegyzés: A 10-es számrendszerben írt véges tizedestört konvertált alakja nem minden esetben véges.
Feladat
Írja fel a tízes számrendszerben azokat a számokat, amelyek a tizenegyes számrendszerben \(\overline{a0b}\), a kilences számrendszerben pedig \(\overline{b0a}\) alakban írhatók fel.
(Összefoglaló feladatgyűjtemény 3975. feladat.)
A megadott értékek így írhatók fel:
\(\overline{a0b}\)=a0b11=a⋅112+0*111+b*110, Itt 0<a,b <11 egész számok,
\(\overline{b0a}\)=b0a11=b⋅92+0⋅91+a⋅90. Itt pedig 0<a,b <9 egész számok.
Vagyis: a⋅112+0*111+b⋅110= b⋅92+0⋅91+a⋅90. Azaz 121a+b=81b+a egyenletet kapjuk, ahol a,b <9.
Ezt átrendezve: 120a=80b. Egyszerűsítve: 3a=2b Ezt azt mutatja, hogy b-nek 3-mal, a-nak 2-vel oszthatónak kell lennie. A lehetséges értékek: b= 3 vagy 6, a=2 vagy 4.
A megoldások tehát 20311=2⋅112+0⋅111+3⋅110=2⋅121+3=24510=3029=3⋅92+0⋅91+2⋅90=3*81+2= 24510 illetve:
40611=4⋅112+0⋅111+6⋅110=4⋅121+6=49010=6049=6⋅92+0⋅91+4⋅90=6⋅81+4=49010.
Ha ezek után kedved van megfejteni egy rejtélyes életrajzot, katt ide.
Régi korok számírásairól
Bár számunkra természetes és megszokott a tízes számrendszer, ez azonban csak fokozatosan alakult ki. Több minden őrzi mai napig egyéb számrendszerek emlékét. Gondoljunk az idő, illetve szög mérésénél alkalmazott 60-as váltásra: 60 másodperc 1 perc, 60 perc 1 óra. A tízes számrendszerünk hindu eredetű, amely arab közvetítéssel jutott el Európába a középkorban. A régebbi időkben az egyes kultúrák más-más módon számoltak.
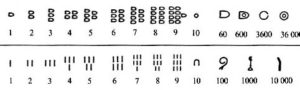
Egyiptom
Az ókori Egyiptomban négy számjeggyel le tudták írni a számokat egészen 10000-ig. Külön jelük volt az egyre ( |: egy pálcika), a tízre (∩ : egy fordított U alak), a százra, és az ezerre. Így tehát számrendszerük 10-es számrendszer volt, de helyértéket nem használtak.
Babilon, Mezopotámia
Mezopotámiában, Babilonban alapvetően 60-as számrendszert használtak. 1-től 59-ig nem helyértékes módon jelölték a számokat, úgy, hogy a 10-re külön jelük volt. 60-tól 60-as helyértékes számrendszerben számoltak.
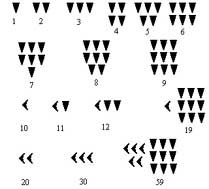 |
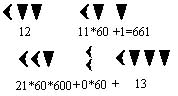 |
| Babilóniai számjegyek | Helyi értékek használata Mezopotámiában |
A 60-as számrendszer nyomait fedezhetjük fel a szögek és az idő mérésénél is.
A szög fokban történő mérésénél 60 a váltószám. (1°=60 szögperc, 1 szögperc 60 szögmásodperc).
Hasonlóan az időnél (1 óra=60 perc, 1 perc= 60 másodperc).
Lásd: https://hu.wikipedia.org/wiki/Hatvanas_sz%C3%A1mrendszer
Ókori görögök számírása

Az ókorban a görögöknél is a 10-es, de nem helyértékes számrendszer alakult ki. A számokat is az abc betűivel jelölték. Az első 9 számot az abc első 9 betűjével jelölték, a következő 9 betű a 9 darab tízest jelentette, majd 9 darab százast újabb betű. Mivel azonban az abc csak 24 jelből állt, 3 számra külön jelük volt. A szavak és a számok megkülönböztetése érdekében a számot jelentő szó fölé vízszintes vonalat húztak. Az ezreseket is ugyanezekkel a betűkkel jelölték, de vesszőt tettek eléje. 5342=\(\overline{,ετμβ}\).
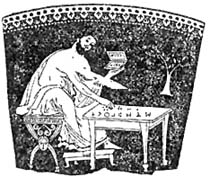
Az ókori népek, így a görögök számolást segítő eszköze is az abakusz volt. A jobboldali képen egy görög adószedő látható, amint abakuszon számol.
Római számírás

A rómaiak szintén 10-es, de nem helyértékes számrendszerben írták a számokat, de külön jelük volt még az 5, 50 és 500-as értékekre.
Az európai kultúrában még ma is ismertek a római számjegyek.
I, II, III, IV, V, VI, VII, VIII, IX, X, XI=11, XX=20, L=50, C=100, D=500, M=1000.
Különösen épületek homlokzatán gyakori, hogy az épület elkészülésének dátumát római számjegyekkel írták fel, még jóval indo-arab számjegyek elterjedése után is.
A maják számírásáról:

A 3. századból származó leletek tanúsága szerint a maják a 20-as, helyértékes számrendszert használtak. Sőt ebből többféle is elterjedt volt. 1-től 19-ig megvoltak a mellékelt ábrán látható jeleik. A nullát is jelölték.
 A jobboldali felső ábrán azt láthatjuk, hogy a maják hogyan írták a 20-t. A kagyló-forma jelöli a nullát, felette pedig a „húszas” helyértéken láthatjuk az 1-t.
A jobboldali felső ábrán azt láthatjuk, hogy a maják hogyan írták a 20-t. A kagyló-forma jelöli a nullát, felette pedig a „húszas” helyértéken láthatjuk az 1-t.
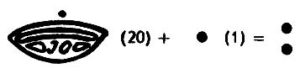 Itt pedig a 20+1=21 látható.
Itt pedig a 20+1=21 látható.
Egymás felett egy-egy egyes jelzi a 21-es számot.

Itt pedig a másik fajta számírásukat, az un. fej-számokat láthatjuk.

A maják is használtak a számoláshoz segédeszközt. Az ő abakuszuk „zsinóros” volt. Különböző számú csomó különböző értéket képviselt. Lehet, hogy innen ered: „Csomót kötök a zsebkendőmre….”?
Hinduk számírásáról:
A hinduk ugyan tízes számrendszert használtak, de kezdetben helyérték nélkül. Az i.sz. III.-VI. század táján történt, hogy helyértékes számrendszerben kezdtek számolni. A tízes számrendszer tőlük arab közvetítéssel jutott el Európába a X. és XI. században.


Comments are closed, but trackbacks and pingbacks are open.