Bevezető példa:
Írjuk fel a következő expilicit módon megadott számsorozat első néhány elemét: an=3⋅n+1. Az első öt tag: a1=4; a2=7; a3=10; a4=13; a5=16…
Látható, hogy a minden tag az előzőhöz képest 3-mal több.
Így a fenti sorozat rekurzív módon is megadható. Megadjuk az első elemét és a képzési szabályt: a1=4; an=an-1+3.
Definíció:
Számtani sorozatoknak nevezzük azokat a sorozatokat, amelyekben (a másodiktól kezdve) bármelyik tag és az azt megelőző tag különbsége állandó.
Ezt az állandó különbséget a sorozat differenciájának nevezzük, és általában d-vel jelöljük.
Formulával: a1; an=an-1+d (n>1).
Számtani sorozat jellemzése:
A számtani sorozat tulajdonságai (korlátossága, monotonitása) csak a differenciájától (d) függ.
1. Ha egy számtani sorozatnál d>0, akkor a sorozat szigorúan monoton növekvő és alulról korlátos.
2. Ha d<0, akkor a számtani sorozat szigorúan monoton csökkenő és felülről korlátos.
3. Ha pedig d=0, akkor a számtani sorozat nemnövekvő, nemcsökkenő, azaz állandó.
A számtani sorozat csak abban az esetben konvergens (csak akkor van határértéke), ha konstans, azaz d=0.
Számtani sorozat elnevezéséről:
Miért hívják így az ilyen típusú sorozatokat? A Fibonacci sorozatot egy matematikusról nevezték el.
Írjuk fel egy számtani sorozat három szomszédos elemét: an-1; an; an+1.
Ezt a definíció szerint így is írhatjuk: an-d; an; an+d.
Adjuk össze az an-1 és az an+1 tagokat! an-1 + an+1= an-d + an+d= 2⋅an.
Ami azt jelenti, hogy: \( a_{n}=\frac{a_{n-1}+a_{n+1}}{2} \ \), ahol n>1.
Vagyis a számtani sorozat n-edik (nem első) tagja vele szomszédos két tag számtani közepe. Sőt ezt általánosabban is írhatjuk: \( a_{n}=\frac{a_{n-i}+a_{n+i}}{2} \), ahol n>i és n>1.
Amit úgy is fogalmazhatunk, hogy a számtani sorozat n-edik eleme (n>1) számtani közepe a tőle szimmetrikusan elhelyezkedő két másik tagnak.
Számtani sorozat n-edik tagjának meghatározása
Állítás:
A számtani sorozat n-edik tagja: an=a1+(n-1)d.
Az állítás helyességét teljes indukcióval fogjuk belátni. Közben felhasználjuk a sorozat definícióját, miszerint: an=an-1+d.
Bizonyítás:
1. A definíció felhasználásával belátjuk konkrét n értékekre:
Az állítás n=2 esetén a definícióból következően igaz: a2=a1+d.
Az állítás n=3 esetén is igaz, hiszen a3=a2+d=a1+d+d=a1+2⋅d.
2. Az indukciós fetételezés: „n” olyan n érték, amelyre még igaz:
an=a1+(n-1)d. Ilyen az előző pont szerint biztosan van.
3. Ezt felhasználva, bebizonyítjuk, hogy a rákövetkező tagra is igaz marad, azaz: an+1=a1+nd. Tehát azt, hogy a tulajdonság öröklődik.
Definíció szerint ugyanis az n-edik tag után következő tag: an+1=an+d.
Az an értékére felhasználva az indukciós feltevést: an=a1+(n-1)d+d.
Zárójel felbontása és összevonás után: an+1=a1+nd.
Ezt akartuk bizonyítani.
Számtani sorozat tagjainak összege
Állítás:
A számtani sorozat első n tagjának összege: \( S_{n}=\frac{(a_{1}+a_{n})·n}{2} \).
Bizonyítás:
A számtani sorozat első n tagjának összegét (Sn) Gauss módszerével fogjuk belátni.
Írjuk fel az első n tag összegét tagonként, majd még egyszer, fordított sorrendben is.
Sn=a1+a2+a3+…+an-2+an-1+an
Sn=an+an-1+an-2+…+a3+a2+a1.
Adjuk össze a kapott összefüggéseket, így n darab kéttagú kifejezésből álló kifejezést kapunk a jobb oldalon:
2⋅Sn=(a1+an)+(a2+an-1)+(a3+an-2)+…+(an-2+a3)+(an-1+a2)+(an+a1).
Itt minden zárójelben szereplő közbülső tagot fel tudunk írni an és a1 segítségével:
a2+an-1=a1+d+an-d=a1+an
a3+an-2=a1+2d+an-2d=a1+an
és így tovább.
Tehát az összegben n-szer szerepel az (a1+an) tag, és a d kiesik. Így:
2⋅Sn=n⋅(a1+an) .
Kettővel átosztva, az állításhoz jutunk: \( S_{n}=\frac{(a_{1}+a_{n})·n}{2} \).
A gyermek Gauss-sal kapcsolatos a következő közismert történet:
Az akkori időkben egy tanító egyszerre több osztállyal foglalkozott. Amíg a tanító az egyik csoporttal foglakozott, addig a többieknek önálló feladatot adott. Egy alkalommal Gauss csoportja azt a feladatot kapta, hogy adják össze 1-től 40-ig az egész számokat. A tanító arra számított, hogy ez jó sokáig el fog tartani a gyermekeknek. Legnagyobb csodálkozására a kis Gauss már jelentette is az eredményt: 820. A tanító kérdésére, hogy kapta a helyes eredményt, el is magyarázta: Az első és utolsó szám összege: 1+40=41. A második és utolsó előtti számok összege: 2+39=41. 20 darab ilyen pár van, mindegyik összege 41, így a keresett összeg 41⋅20=820.
A tanító nem sajnálta a fáradtságot, jelentette az esetet, így a kisfiú híre hamar elterjedt.
Ha egy szőnyeget feltekerünk, arkhimédészi spirált kapunk. A keletkező henger átmérőjének kiszámítása egy számtani sorozat összegének meghatározását jelenti.
Feladat:
Egy 5 cm átmérőjű rúdra felcsavarunk 20 m szövetet. A szövet vastagsága 1 mm. Mekkora a keletkező henger átmérője?
(Összefoglaló feladatgyűjtemény 3539. feladat.)
Megoldás:
Mivel a rúd átmérője 5 cm = 50 mm, ezért a rúd kerülete: 50π mm.
Egyszeri körültekerés után a henger átmérője 2 mm-rel nő, azaz 52 mm lesz, ezért a kerülete 52π mm lesz.
Minden további tekeréskor az átmérő 2 mm-rel, ezért a rúd kerülete 2π mm-rel fog nőni.
Az egyes tekerésekkor kapott kerületek olyan számtani sorozatot alkotnak, amelynek első tagja: a1=50π, a2=52π, és így tovább. A differencia: d=2π.
A kérdés úgy is fogalmazható, hogy hány tekeréssel lehet a 20 m = 20 000 mm hosszúságú szövetet feltekerni. Ez az érték az egyes tekerésekkor fellépő kerületi értékek összege lesz, Tehát Sn= 20 000.
Felhasználva a megismert összefüggéseket: \( S_{n}=\frac{(a_{1}+a_{n})·n}{2} \), és an=a1+(n-1)d.
Ebből a két összefüggésből:
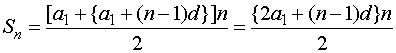
A példában most az Sn adott (Sn= 20 000), és az n az ismeretlen.
Sn= 20 000; a1=50π; d=2π értékeket behelyettesítve:
20 000=n(2⋅50π+(n-1)⋅2π)/2.
Kettővel átszorozva: 40 000=n⋅(2⋅50π+(n-1)⋅2π).
A belső zárójelet felbontva, összevonva: 40 000=n⋅(98π+2π⋅n).
A külső zárójelet felbontva: 40 000=98π⋅n+2π⋅n2.
2π-vel átosztva: 20 000/π=n2+98π⋅n.
Az így kapott n-re másodfokú egyenletetet 0-ra redukálva és a megoldóképlettel megoldva, (a=1; b=49; c=20 000/π), annak pozitív gyöke megközelítőleg n≈59.
Ez azt jelenti, hogy körülbelül 59-szer lehet a 20 m-es anyagot az 5 cm átmérőjű rúdra feltekerni. Az utolsó tekeréskor a rúd kerülete: a59=a1+58⋅d összefüggés felhasználásával a59=50π +58⋅2π, a59=166π.
Így ekkor az átmérő≈166 mm lesz, ami az üres rúd átmérőjének több mint 3-szorosa.
Megjegyzés: Az ókori Görögországban Pitagorasz követői a püthagoreusok már tudták a számtani sorozatot összegezni.


Comments are closed, but trackbacks and pingbacks are open.