Ezt a sorozatot az olasz Fibonacci-ról nevezték el, mert ő fogalmazta meg a következő feladatot:
„Hány pár nyúl származhat egy évben egyetlen pártól, ha minden pár havonta új párnak ad életet, amely a második hónaptól lesz tenyészképes, és feltételezzük, hogy egy ivadék sem pusztul el?”
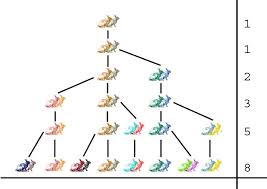 A válasz a következő sorozat: 1, 1, 2, 3, 5, stb. Azaz h1=1, h2=1, h3=2, h4=3, h5=5,… stb. Tehát az első két hónapban (h1, h2) még csak a „kezdő” párunk van, a harmadik hónapban születik meg az első új pár. A negyedik hónapban ez az új pár még nem ellik, de szülei igen, így már három pár nyulunk van. És így tovább.
A válasz a következő sorozat: 1, 1, 2, 3, 5, stb. Azaz h1=1, h2=1, h3=2, h4=3, h5=5,… stb. Tehát az első két hónapban (h1, h2) még csak a „kezdő” párunk van, a harmadik hónapban születik meg az első új pár. A negyedik hónapban ez az új pár még nem ellik, de szülei igen, így már három pár nyulunk van. És így tovább.
Fibonacci sorozathoz jutunk akkor, ha azt számoljuk, hogy egy lépcsőn felfelé haladva hányféleképpen juthatunk fel az n-edik lépcsőfokra, ha feltételezzük, hogy egyszerre csak egy, de legfeljebb két lépcsőfokot tudunk lépni.
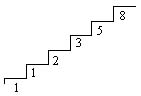 Tekintsük a kiindulási helyzetünket az első lépcsőfoknak. Ez az első tagja a sorozatnak, f1=1. A második lépcsőre lépni csak egy lehetőségünk van, nevezetesen a kiindulási pontról, ezért f2=1. A harmadik lépcsőre kétféleképpen juthatunk fel, a kiindulási pontról és az második lépcsőről, tehát f3=2. A negyedik lépcsőre a harmadikról vagy a másodikról juthatunk. A másodikra 1, a harmadikra 2, így a negyedikre 3 lehetőségünk van. És így tovább. A mellékelt ábrán a lépcsők alatti számok mutatják, hogy arra lépcsőfokra hány lehetőségünk van feljutni.
Tekintsük a kiindulási helyzetünket az első lépcsőfoknak. Ez az első tagja a sorozatnak, f1=1. A második lépcsőre lépni csak egy lehetőségünk van, nevezetesen a kiindulási pontról, ezért f2=1. A harmadik lépcsőre kétféleképpen juthatunk fel, a kiindulási pontról és az második lépcsőről, tehát f3=2. A negyedik lépcsőre a harmadikról vagy a másodikról juthatunk. A másodikra 1, a harmadikra 2, így a negyedikre 3 lehetőségünk van. És így tovább. A mellékelt ábrán a lépcsők alatti számok mutatják, hogy arra lépcsőfokra hány lehetőségünk van feljutni.
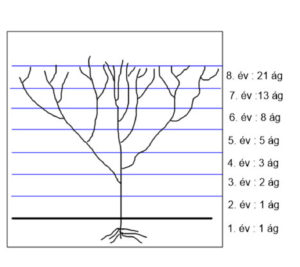
A sorozat szemléltetésére szokták még a következő példát mondani:
Egy fa az ültetést követő második évben hoz először új ágat. Minden ág a keletkezését követő évben csak gyarapszik, és az azt követő évektől kezdve minden évben egy újabb ágat hoz. Hány ága lesz a fának 5, 10, n év múlva?
Megjegyzés: Ez a példa természetesen nem jeleni azt, hogy bármely konkrét fafajtánál az ágak ilyen szabály szerint hajtanának.
Általánosítva:
Fibonacci sorozatoknak nevezzük azokat a sorozatokat, amelyeknél az első két tag adott, ezt követően minden tag az őt megelőző két tag összege.
Formulával: Adott f1 és f2, (f1=f2=1 ) és fn=fn-1+fn-2.
A sorozat első néhány eleme:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465, …
Fibonacci sorozat tulajdonságai:
Korlátossága: Mivel minden tagja pozitív, alulról korlátos, minden tagja nagyobb 1-nél. Ugyanakkor felülről nem korlátos.
Menete: A definícióból következik, hogy a sorozat monoton növekszik, sőt a harmadik tagtól kezdve szigorúan monoton.
Fibonacci sorozat első néhány tagjának ábrázolása koordináta-rendszerben.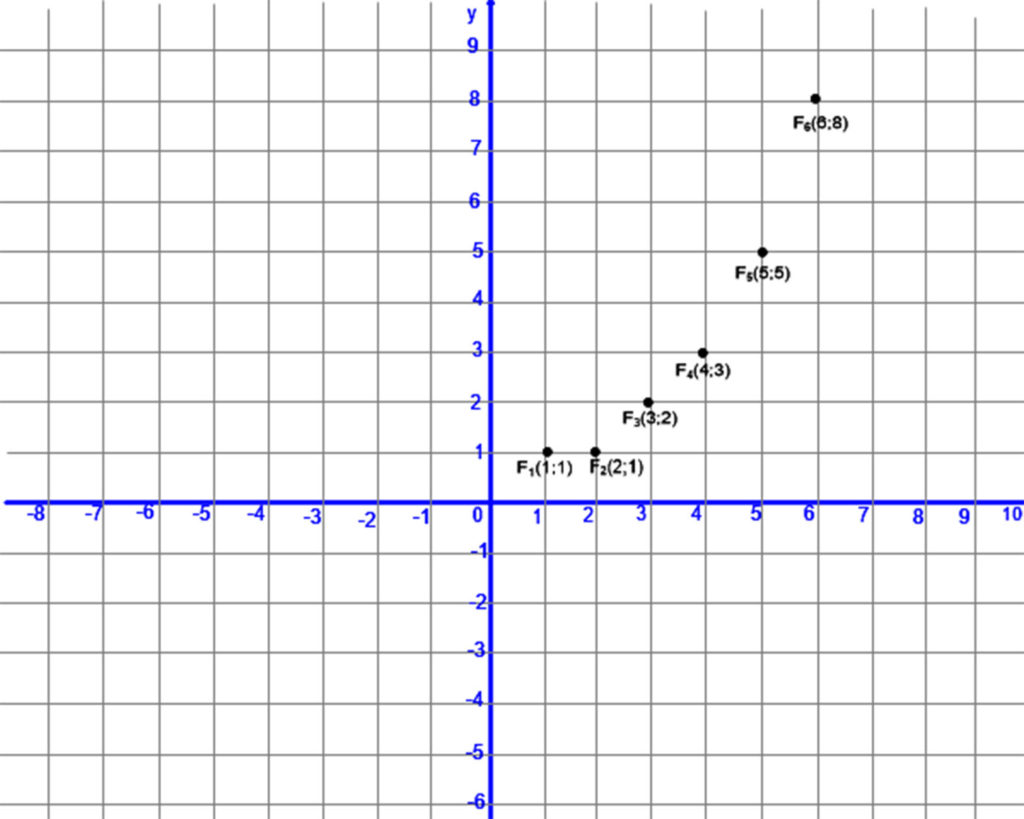
Fibonacci sorozat első néhány tagjának ábrázolása számegyenesen.
További ismeretek a Fibonacci sorozatról.
(Lásd: Gerőcs László: A Fibonacci sorozat általánosítása;
illetve Sokszínű matematika 12.)
Néhány ezek közül:
-
- A sorozat n-edik eleme eggyel nagyobb, mint a sorozat első n-2 elemének az összege.
- A páratlan indexű tagok összege megegyezik a rákövetkező elemmel.
- Minden negyedik eleme osztható 3-mal. Formulával: 3|fn; n=4⋅k, k∈ℕ+.
- A sorozat első „n” tagjának az összege megegyezik az „n”-dik és a rákövetkező tag szorzatával.
- A Fibonacci sorozat kapcsolatban van az aranymetszéssel, nevezetesen a sorozat egyre nagyobb sorszámú elemeinek hányadosa egy állandó számhoz, az aranymetszéssel kapott hosszabbik szakasznak a rövidebbikhez való arányához közelít.
A Fibonacci-sorozat két szomszédos elemének hányadosan az aranymetszés arányszámához (1.618-hoz)„közelít”. Formulával: \( \frac{a_{n+1}}{a_{n}}→\frac{1+\sqrt{5}}{2}≈1.618 \).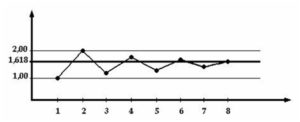
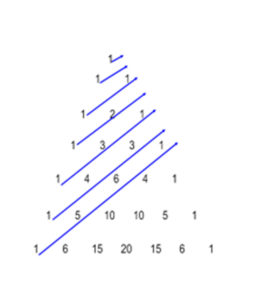 A Fibonacci sorozat a Pascal-háromszöggel is kapcsolatban van. Ha a mellékelt ábrán követjük a nyilakat és összeadjuk a nyilak mentén található binomiális együtthatókat, akkor a következő összegeket kapjuk:
A Fibonacci sorozat a Pascal-háromszöggel is kapcsolatban van. Ha a mellékelt ábrán követjük a nyilakat és összeadjuk a nyilak mentén található binomiális együtthatókat, akkor a következő összegeket kapjuk:
\( \binom{0}{0}=1=f_{1}; \; \binom{1}{0}=1=f_{2}; \; \binom{2}{0}+\binom{1}{1}=2=f_{3}; \; \binom{3}{0}+\binom{2}{1}=3=f_{4} \). És így tovább: \( \binom{6}{0}+\binom{5}{1}+\binom{4}{2}+\binom{3}{3}=\sum_{i=0}^{3}\binom{6-i}{i}={ }1+5+6+1=13=f_{7} \).Általában: \( f_{n+1}=\sum_{i=0}^{\left [\frac{n}{2}\right ] }{ }\binom{n-i}{i} \).Kérdéses, hogy a Fibonacci-sorozat tagjai között végtelen sok prímszám van-e. A Fibonacci sorozat első néhány tagjában megjelölve a prímszámokat:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584,…


Comments are closed, but trackbacks and pingbacks are open.