Számsorozat fogalma

Hogyan folytatnád?

Az alábbi néhány számsorozatot nagyon könnyű folytatni.

a)   2, 4, 6, …
b) 2;-6;18;
c) 3; 5; 7;….

Vegyük azonban észre, hogy ezeknél a fenti feladatoknál a folytatás nem is annyira egyértelmű. Például  így is folytathatnánk:

a)   2, 4, 6,  2, 4, 6, ,… és így tovább.
b) 2;-6;18, 2,-6,18,… és így tovább.
c) 3; 5; 7, 3, 5, 7,… és így tovább.

A harmadik (A c) jelű) sorozatra legtöbben a következő folytatást javasolnák:
3; 5; 7, 9, 11, 13,… és így tovább. Azaz a páratlan egész számok sorozatára gondolnának. Pedig a c) 3; 5; 7, sorozat így is folytatható:
3, 5, 7, 11, 13, 17, 19,… és így tovább.  Ez pedig a páratlan prímszámok sorozatát jelenti.

Gyakori kérdés , hogy milyen szám állhat a megadott számsorozat egy adott sorszámú helyén. Ez a kérdés azonban feltételezi, hogy a sorozat folytatása  egyértelmű.

Ha c) feladatban a páratlan egész számok sorozata van megadva, akkor a 10. helyen a 21-es szám áll. Ha a c) feladatban a számsorozat a páratlan prímek sorozata, akkor a 10. helyen a 31-es szám van.

Megjegyzés:

Ezek a sorozatok vég nélkül folytathatók.  A c) jelű sorozat is, hiszen bizonyított tény, hogy végtelen sok prímszám van, de a prímszámok sorozata jelenleg is csak egy adott számig ismert hiánytalanul. Eltekintve az eratoszthenészi szitától, nincs olyan képzési szabály, amely a prímszámok sorozatát előállítaná.

A számsorozatoknál tehát egy adott sorszámhoz egyértelműen tartozik hozzá a sorozat adott sorszámú eleme.

Sorozat fogalma:

A számsorozat a pozitív egész számok halmazán értelmezett valós értékű függvény. f: ℕ⁺→ℝ.

Másképpen: Ha egy függvény értelmezési tartománya a pozitív egész számok halmaza, értékkészlete a valós számok egy részhalmaza, akkor ezt a függvényt valós számsorozatnak, vagy röviden sorozatnak nevezzük. f: ℕ⁺→ℝ.
A számsorozat tehát egy speciális függvény.

Jelölések:

Sorozatok esetében egy sajátos jelölési mód alakult ki. A sorozatot az ABC kis betűivel szoktuk azonosítani. Elemei esetében az alsó index jelöli, hogy a számsorozat adott eleme melyik sorszámhoz tartozik, azaz a sorozat, mint függvény változóját az alsó indexben szerepeltetjük.

A kiinduló c) jelű példánál maradva legyen a számsorozat jele {c_n}, elemeit pedig így jelöljük: c₁; c₂;… c_n azaz c₁=3; c₂=5;….; c_n= az n-edik prímszám.
Az c_n a sorozat n-edik tagját, az  {c_n} magát a sorozatot jelöli.

Számsorozatok megadása módjai:

Mivel a számsorozat függvény, a megadási módok is hasonlóan a függvényekhez igen változatosak.

Számsorozat megadható:

Elemei (egyrészének) felsorolásával képlettel; és/vagy szövegesen is. Természetesen a sorozat megadásnak egyértelműnek kell lennie. Ugyanazt a sorozatot adott esetben többféle módon definiálhatjuk.
Elemeinek felsorolásával: {d_n}=1; 4; 9; 16; 25; … (ha az egyértelmű).
Képlettel, ha lehetséges: {e_n}=2n+1, ahol n∈ℕ⁺; e_n∈ℤ⁺.
Szövegesen: {p_n}={A prímszámok sorozata}. Nincs képlet. Ugyanakkor p_n=?.
A {d_n} sorozat megadása szövegesen:  {d_n}={ A négyzetszámok sorozata}.
A képlettel megadott sorozatoknál a képlet alapján felírhatók a sorozat elemei.

Mi a közös az alábbi sorozat meghatározásokban?
g) g₁=3; g_n=g_n-1+n. (n>1) Azaz: 3, 5, 8, 12; …
f) f₁=1; f₂=1; f_n=f_n-1+ f_n-2. Azaz: 1; 1; 2; 3; 5; 8; 13; …

Ezekben az esetekben a sorozat elemeit az előző tagok ismertében határozzuk meg. A fenti sorozatok un. rekurzív sorozatok. Pontosabban rekurzív módon megadott sorozatok. A második (f) jelű sorozat a nevezetes Fibonacci sorozat.

Számsorozatok ábrázolása

Mivel a számsorozat egy speciális függvény ezért ez történhet koordináta rendszerben is.  Gyakoribb azonban a számegyenes való ábrázolás. A sorozat grafikonja természetesen – definícióból következően – diszkrét pontokból áll. Itt a pontok első koordinátája a sorozat tagjának a sorszáma, a második koordináta pedig a sorozat adott sorszámú tagjának az értéke.

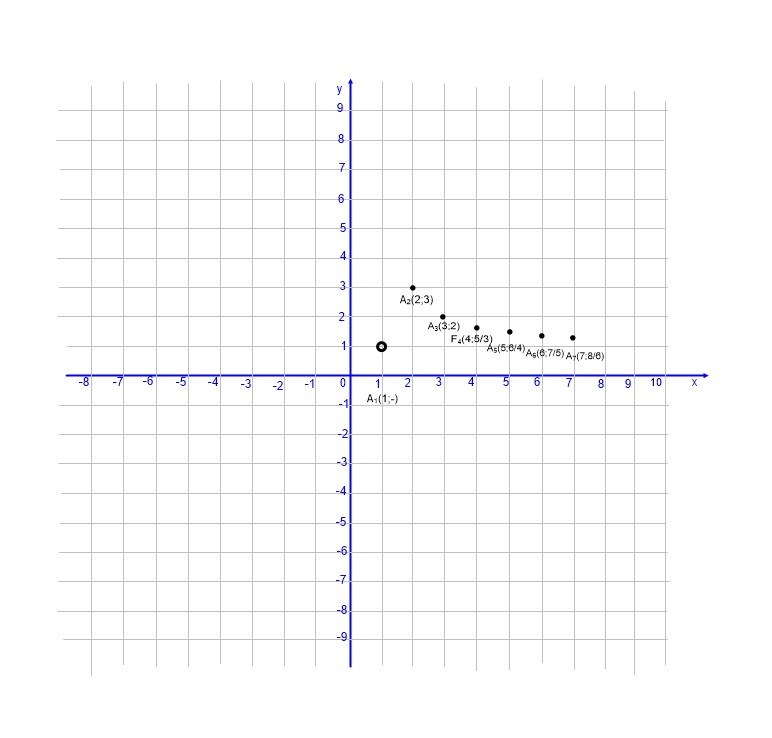
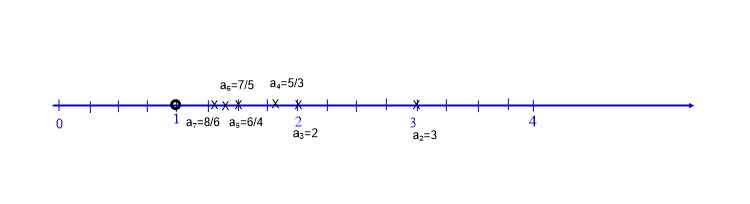
Ábrázoljuk a következő sorozatot: ​\( a_{n}=\left\{\frac{n+1}{n-1} \right\}=\left\{ 1+\frac{2}{n-1}\right\} \; n∈\mathbb{N}^{+} \; n>1 \)​.

Azaz: a₁=/ (nincs), a₂=3, a₃=2, a₄=5/3, a₅=6/4=3/2, a₆=7/5, a₇=8/6=4/3, ….és így tovább.

Koordináta rendszerben történő ábrázolás:

Számegyenesen történő ábrázolás: