Német matematikus, csillagász és fizikus. Őt tartják minden idők egyik legnagyobb matematikusának. Így is nevezik: „A matematikusok fejedelme.” Euler mellett ő a matematika legsokoldalúbb tudósa.
Gauss életéről
Braunschweigben született, édesapja nyergesmester volt. Már 6 éves korában kitűnt matematikai tehetségével.
Tanítója egyszer azt a feladatot adta a kis tanulóknak, hogy adják össze a számokat 1-től 40-ig, mivel a tanító úr addig egy másik évfolyammal akart foglalkozni, és így akarta addig a kicsiket lefoglalni. De a kis Gauss hamarosan jelentkezett a jó eredménnyel. Csodálkozó tanítójának el is magyarázta, hogyan csinálta. Párba állította a számokat 40+1=39+2=38+3 stb. Ezek a párok mindig 41-t adnak összegül, és mivel 20 ilyen pár van, az eredmény 820.
Ez a gondolkozás megegyezik a számtani sorozat összegének meghatározásánál alkalmazottal. Tanítója felismerve a kisfiú rendkívüli képességeit, jelentette az esetet elöljáróinak. Így jutott el a híre braunschweig-i herceghez, aki felkarolta a kis Gauss-t. Gimnáziumba került, majd a göttingeni egyetemre. Pályája töretlenül ívelt felfelé. Ismerte és barátjának nevezte Bolyai Farkast, ennek ellenére fiát Bolyai Jánost nem támogatta és evvel igen nagy csalódást okozott mindkettőjüknek. Sajnos Gauss mások elismerésével is fukarkodott. Így például Abel tehetséges norvég matematikussal kapcsolatban is. Lobacsevszkij orosz matematikust ugyan beajánlotta a Göttingeni Tudományos Társaságba, de a nem euklideszi geometria megalkotásának területén végzett munkásságának közvetlen elismeréstől tartózkodott, akárcsak Bolyai János esetében.
Gauss békés, hosszú és elismert életet élt. Igazi zsenialitást még így is nehéz teljes egészében felmérni, mert nagyon sok felfedezését, elgondolását, így a nem euklideszi geometria felfedezése irányába tett gondolatait sem publikálta.
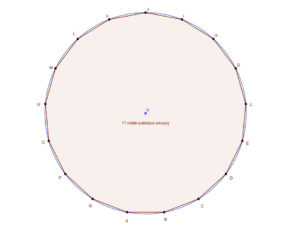
Németország Göttingen városában az Albani temetőben (Albani-Friedhof) nyugszik. Utolsó kívánsága az volt, hogy egyik korai és számára legkedvesebb felfedezésének, a 17 oldalú szabályos sokszög szerkesztésének emlékére sírkövére egy szabályos 17 szöget véssenek. Ezt ugyan nem teljesítették, de szülővárosában a tiszteletére emelt szobor talapzatán látható a szabályos 17 oldalú sokszög.
Gauss csillagászként is számottevőt alkotott. 1801-ben egy új és egyszerűbb módszert dolgozott ki a bolygó pályájának kiszámítására. 1820 körül geodéziával (földmérés) kezdett foglalkozni. Fizikai munkássága is említésre méltó. Göttingenben egy szobor ábrázolja őt és Wilhelm Webert a távíró 1833-ban történő feltalálása közben. Ő alkotja meg az első abszolút fizikai mértékegységrendszert. Még számológép fejlesztéssel foglalkozott, Leibniz gépét tökéletesítette. Ez a gép az ő idejében népszerű volt egész Németországban.
Gauss matematikai munkásságáról
Egyik legkedvesebb matematikai szakterülete a számelmélet volt. Tőle származik az a mondás, hogy: „A matematika a tudományok királynője, és a matematika királynője a számelmélet.” 1791-ben, 14 éves korában becslést adott a prímszámok eloszlására, miszerint ezres számkörben a prímszámok száma fordítottan arányos a számok természetes alapú logaritmusával. Ezt ugyan később többen is pontosították, de ez semmit nem von le a fiatal Gauss érdemeiből.
Ő volt az, aki felfedezte, hogy kapcsolat van a prímszámok és a szabályos sokszögek szerkeszthetősége között. Egy „n” oldalszámú szabályos sokszög csak akkor szerkeszthető euklideszi szerkesztéssel ha „n” prímtényezős felbontásában csak a 2 szerepel tetszőleges nem-neagatív egész kitevőjű hatványon, és az un. Fermat-féle prímek (3,5,17,65537) első kitevőjű hatványon. Azaz n=2k⋅p1⋅p2⋅…⋅pk, ahol p1, p2, pk különböző Fermat-féle prímek. Tehát szerkeszthető a 3, 4, 5, 6, 8, 10, 12, 14, 15, 17, …, 257 és 65537 oldalú szabályos sokszög, de nem szerkeszthető például a 7, 9 , ill. 11 oldalú. A 17 oldalú szabályos sokszög szerkesztésének a módját ő meg is oldotta.
Gauss foglalkozott a szakaszos tizedes törtekkel, és tisztázta mikor kapunk tiszta vagy vegyes szakaszos tizedes törtet, és mekkora lehet a szakasz hosszúsága. 1799-ben a doktori értekezésében az „algebra alaptételét” igazolta, amely szerint minden algebrai egyenletnek van gyöke. Ezek gyökök nem okvetlenül valósak, hanem lehetnek komplex számok is, és nem biztos, hogy ezek a gyökök mind különböznek egymástól. A gyökök száma (beleértve az azonosakat is) az egyenlet fokszámával egyenlő.
1827-ben jelent meg „A görbe felületekre vonatkozó általános vizsgálatok” című műve, amelynek eredményei geodéziai munkásságára vezethetők vissza. Gauss ötlete, hogy a komplex számokat a sík pontjaiként ábrázolhatjuk. 1837-ben megjelent értekezése a komplex számok algebráját és aritmetikáját tartalmazza. A nem euklideszi geometria megalkotásának területén végzett kutatásairól csak levelezéseiből tudunk és feltételezhető, hogy ezen a területen is messzire jutott.
Comments are closed, but trackbacks and pingbacks are open.