Bizonyítási módszerek

Bizonyítási módszerek a matematikában.

Matematikában az axiómákon kívül minden állítást bizonyítunk.
De ennek többféle módja van. Nézzük az alábbiakat:

1. Direkt bizonyítás
2. Indirekt bizonyítás
3. Teljes indukció
4. Skatulya-elv

1. Direkt bizonyítás.

Ebben az esetben már korábbi bizonyított állításokból illetve axiómaként elfogadott alapállításokból kiindulva, helyes logikai következtetések alapján bizonyítjuk az állítást.  A leggyakrabban alkalmazott módszer.

Példa a direkt bizonyítás alkalmazására. 

Állítás: A háromszög területe=oldal⋅szorozva a hozzátartozó magassággal és osztva 2-vel, azaz:  ​\( t_{Δ}=\frac{a·m_{a}}{2}=\frac{b·m_{b}}{2}=\frac{c·m_{c}}{2} \)​

Bizonyítás:

Ennek az állításnak a bizonyításánál felhasználjuk azt a már bizonyított tételt, hogy a paralelogramma területe alap⋅magasság (vagyis: ​\( t=a·m_{a} \)​ , valamint azt, hogy a középpontos tükrözéskor szakasz képe vele párhuzamos szakasz.

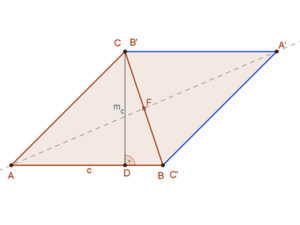Legyen adott az ABC háromszög. Tükrözzük ezt a háromszöget a BC szakasz F felező pontjára. Ekkor B’=C és C’=A. Az AB szakasz képe a C’A’, az AC szakasz képe B’A’. Tehát az ABA’C négyszög olyan paralelogramma, amelynek egyik oldala a háromszög AB oldala és paralelogramma magassága megegyezik a háromszög magasságával. A középpontos tükrözés miatt az t_ABC=t_A’B’C’ Vagyis a kapott paralelogramma területe éppen kétszerese a háromszög területének.

2. Indirekt bizonyítás.

Az indirekt bizonyítás olyan eljárás, melynek során feltesszük, hogy a bizonyítandó állítás nem igaz és ebből kiindulva helyes következtetésekkel lehetetlen következményekhez jutunk el. Így a kiinduló feltevés volt téves, vagyis a bizonyítandó állítás valójában igaz.

Példa az indirekt bizonyítás alkalmazására.

Állítás:  Nincs legnagyobb prímszám.

Bizonyítás:

• • Tételezzük fel az ellenkezőjét, azaz tételezzük fel, hogy van legnagyobb prímszám, azaz a prímszámok száma véges. Tegyük fel, hogy „k” darab prímszám van: p₁=2, p₂=3, p₃=5 és a feltételezett utolsó prímszám a k-ik p_k.
  • Szorozzuk össze a feltételezett összes prímszámot: p₁⋅p₂⋅p₃⋅….⋅p_k, majd adjunk hozzá 1-t!
    Az így kapott N=p₁⋅p₂⋅p₃⋅….⋅p_k +1 szám vagy prím, vagy összetett.
    • Ha az így képzett N szám prím, akkor különbözik mindegyiktől, amit összeszoroztunk, tehát nem igaz, hogy az összes prímszám szerepel az N szám képzésében.
    • Ha pedig N összetett szám, akkor van prímosztója.
      De az oszthatóság szabályai szerint ez nem lehet egyik sem a p_k-ig terjedő prímszámok között.
  • Van tehát az általunk gondolt összes (k db) prímszámon kívül más prímszám is. Ez ellentmond annak a feltételezésnek, hogy véges számú prímszám van.

3. Teljes indukció:

Ezen a módon olyan állítást bizonyíthatunk, amely az n pozitív egész számoktól függ. Ilyenek például a számtani és mértani sorozat n-edik elemének meghatározására vonatkozó vagy az első n egész szám négyzetösszegére vonatkozó összefüggések. Sok oszthatósággal kapcsolatos állítás is ezen az úton válaszolható meg.

A teljes indukciós bizonyításra 1665-ben Pascal adott pontos meghatározást.

A bizonyítás három fő részből áll:

1. Az állítás igazságáról néhány konkrét n érték esetén (n=1, 2, 3, …) számolással, tapasztalati úton meggyőződünk.
2. Feltételezzük, hogy n az az utolsó olyan pozitív egész szám, amire az állítás még igaz. Ilyen n van, ezt az első lépés biztosítja.
3. Ezt a feltételezést felhasználva bizonyítjuk, hogy a rákövetkező értékre, azaz n+1-re is igaz marad az állítás. (Tehát „öröklődik”, a következő „dominó” is el fog dőlni.)

Példa a teljes indukciós bizonyítás alkalmazására.

Bizonyítsa be, hogy 6|(n²+5)⋅n, (n pozitív egész)!

(Összefoglaló feladatgyűjtemény 3635. feladat.)

Megoldás:

1. Az állítás n=1 esetén igaz, hiszen 6|(12+5)1=6.
2. Tételezzük fel, hogy n az utolsó olyan pozitív egész szám, amire még igaz az állítás.
3. Bizonyítjuk (n+1)-re az öröklődést.

Az (n2+5)n formulába n helyére n+1-t írva:	[(n+1)2+5](n+1)
Zárójeleket felbontva:	(n2+2n+6)(n+1) n3+3n2+8n+6
Más csoportosításban:	(n3+5n)+(3n2+3n+6)
Vagyis:	(n2+5)⋅n+(3n2+3n+6)
Ebben a csoportosításban az első tag osztható 6-tal, az indukciós feltevés miatt.	6|(n2+5)⋅n
A csoportosítás másik tagjában kiemeléssel:	3n⋅(n+1)+6
Itt az n(n+1) tényezők közül az egyik biztosan páros, ezért a 3n(n+1) biztosan osztható 6-tal, így	6|3n2+3n+6.

4. A skatulya-elv

Ha „n” darab objektumot (tárgyat, embert, stb.) „k” darab helyre (skatulyába) helyezünk el (n>k), akkor biztosan lesz legalább egy skatulya, amelybe legalább két objektum kerül.

Általánosabban:

Ha „n” darab objektumot (tárgyat, embert stb.) „k” darab helyre (skatulyába) helyezünk el és n> k*p akkor biztosan lesz legalább egy olyan skatulya, amelybe legalább p+1 objektum kerül.

Példák skatulya-elvvel történő bizonyításra.

I. Bizonyítsuk be, hogy egy 37 fős osztályban biztosan van legalább 4 olyan tanuló, aki ugyanabban a hónapban született.

Megoldás:

Egy évben 12 hónap van (a skatulyák), az osztályban pedig 37 fő tanuló, amely több, mint 3*12=36.
Ha a tanulókat csoportosítjuk születési hónapjuk szerint, akkor a skatulya-elv értelmében lesz legalább egy hónap, amikor 4 tanuló ünnepli a születésnapját.

Gondoljuk csak meg, ha minden hónapra 3 szülinapos jutna, a 37. tanuló már csak olyan hónapban születhetett, ahol már van 3 tanuló.

Megjegyzés: Természetesen lehetnek olyan hónapok, amikor senki nem szülinapos és olyan hónap is, amikor 4-nél többen ünnepelnek. A biztos csak az, hogy van legalább egy hónap, amikor legalább 4 tanuló ünnepel.

II. Bizonyítsa be, hogy egy „n” pontú egyszerű gráfban van két azonos fokszámú pont!  

Bizonyítás:

Mivel az állításban szereplő „n” pontú gráf egyszerű, azaz nincs benne többszörös él és hurok sem, ezért legmagasabb fokszám az n-1 lehet, azaz ebből a pontból minden más pontba vezet él.  De akkor nincs 0 fokszámú elem.
Ha van 0 fokszámú (izolált) elem, akkor a legmagasabb fokszám csak n-2 lehet.
Mind a két esetben n-1 darab fokszám (objektum) létezik az n darab ponthoz (skatulyához), ezért a skatulya-elv értelmében az adott egyszerű gráfban biztosan van két azonos fokszámú pont.

Ezt kellett igazolni.