Bevezető példa:
1. A következő sorozatot nagyon könnyű folytatni: 2; 4; 8; 16,…és így tovább.
Szavakkal: Az első tag 2, minden tag az előző kétszerese.
2. Szerkesszünk egy 3 egység oldalú ABCD négyzetet. Ennek BD átlójára egy újabb négyzetet. És így tovább. Számítsuk ki az egyes négyzetek oldalhosszúságaiból álló sorozat első néhány tagját. Mekkora lesz az ötödik négyzet oldala?
Az első négyzet oldala: a1=3. A következő négyzet oldala az első négyzet átlója, azaz a2=3⋅√2 egység.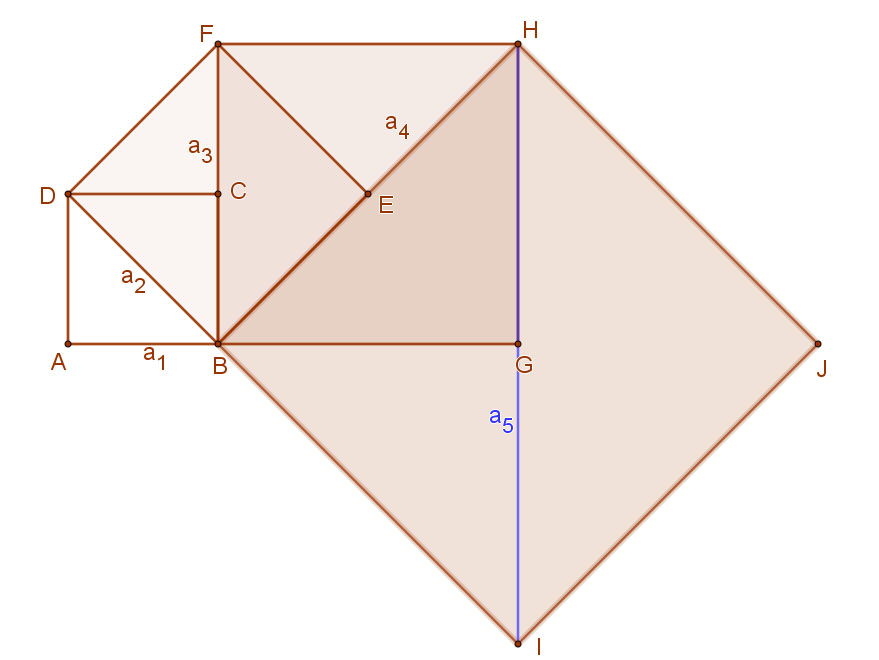
A harmadik négyzet oldala a második négyzet átlója, azaz a3=a2⋅√2=a1⋅√2⋅√2=a1⋅(√2)2=a1⋅2. Azaz a3=6 egység.
Hasonlóan a negyedik négyzet oldala a harmadik négyzet átlójával egyenlő, így a4=a3⋅√2. Az előzőekhez hasonlóan: a4=a1⋅(√2)3. Így a4=6⋅√2.
A következő négyzet oldala tehát a5=a4⋅√2. Így a5=12 egység.
Az egyes négyzetek oldalhosszúságaiból a következő sorozatot kaptuk:
a1=3; a2=3⋅√2; a3=a2⋅√2=6; a4=a3⋅√2; a5=a4⋅√2=12.
Ennek a sorozatnak minden páratlan sorszámú tagja egész szám, míg minden páros sorszámú tag irracionális szám.
Mindkét számsorozatban közös azonban hogy a szomszédos tagok hányadosa konstans. Az első feladatban ez a hányados 2, míg a második feladatnál a egymást követő négyzeteinek oldalhosszúságainak hányadosa √2.
Definíció:
Mértani sorozatoknak nevezzük azokat a sorozatokat, amelyekben (a másodiktól kezdve) bármelyik tag és az azt megelőző tag hányadosa állandó.
Ezt az állandó hányadost latin eredetű szóval a sorozat kvóciensének nevezzük és általában q-val jelöljük.
Formulával: \( \frac{a_{n}}{a_{n-1}}=q \; (n>1) \). Ez szorzat alakban: an=an-1⋅q.
Megjegyzés: A definíció következménye, hogy a mértani sorozat tagjai – az elsőtől eltekintve- egyike sem lehet egyenlő 0-val. Ha sorozat első tagja a1=0, akkor a sorozat minden tagja q-tól függetlenül nulla lenne, de ez ellentmond a definíciónak, hiszen 0-val nem lehet osztani. Ha a1≠0 de q=0, akkor a sorozat nem első tagja mind nullával lesznek egyenlők.
Ezért a továbbiakban feltételezhetjük, hogy a1≠0 és q≠0.
Mértani sorozat jellemzése:
A mértani sorozat viselkedése nemcsak a kvócienstől (q), hanem a sorozat első tagjától is függ.
Ha a mértani sorozat konstans, azaz q=1, vagy c1=0, illetve =0, akkor a sorozat monoton és konvergens.
Ha a mértani sorozat nem konstans (q≠1 és c1≠0), akkor a következő esetek vannak:
1. Ha q>1 és c1>0, akkor a mértani sorozat szigorúan monoton nő, alulról korlátos. A legnagyobb alsó korlát a sorozat első tagja. A mértani sorozat ebben az esetben divergens.
2. Ha q>1 és c1<0, akkor a mértani sorozat szigorúan monoton csökkenő, felülről korlátos. A legkisebb felső korlát a sorozat első tagja. A mértani sorozat ebben az esetben divergens.
3 Ha 0<q<1 és c1>0 , akkor a mértani sorozat szigorúan monoton csökkenő, alulról és felülről is korlátos. A legkisebb felső korlát a sorozat első tagja. A mértani sorozat ebben az esetben konvergens.
4. Ha 0<q<1 és c1<0 , akkor a mértani sorozat szigorúan monoton nő, alulról és felülről is korlátos. A legkisebb alsó korlát a sorozat első tagja. A mértani sorozat ebben az esetben konvergens.
5. Ha –-1<q<0 c1>0, akkor a mértani sorozat nem monoton (oszcilláló), ugyanakkor korlátos. A legkisebb felső korlát a sorozat első tagja.A mértani sorozat ebben az esetben konvergens.
6. Ha -1<q<0 c1<0, akkor a mértani sorozat nem monoton (oszcilláló), ugyanakkor korlátos. A legkisebb alsó korlát a sorozat első tagja. A mértani sorozat ebben az esetben konvergens.
7. Ha q=-1 akkor az első tagjától függetlenül a mértani sorozat nem monoton (oszcilláló) de korlátos. A mértani sorozat ebben az esetben divergens.
8. Ha q<-1, akkor az első tagjától függetlenül a mértani sorozat nem monoton (oszcilláló) és nem is korlátos. A mértani sorozat ebben az esetben divergens.
Mértani sorozat elnevezéséről:
Miért hívják így az ilyen típusú sorozatokat? A Fibonacci sorozatot egy matematikusról nevezték el.
Írjuk fel a sorozat három szomszédos elemét: an-1; an; an+1 (n>1).
Ezt a definíció szerint így is írhatjuk: \( \frac{a_{n}}{q}; \; a_{n}; \; a_{n}·q \).
Képezzük az an-1 ⋅an+1 szorzatot! \( a_{n-1}·a_{n+1}=\frac{a_{n}}{q}·a_{n}·q=a^2_{n} \).
Ami azt jelenti, hogy: \( a_{n}=\sqrt{a_{n-1}·a_{n+1}} \), n>1.
Vagyis a mértani sorozat n-edik (nem első) tagja vele szomszédos két tag mértani közepe. Sőt ezt általánosabban is írhatjuk: \( a_{n}=\sqrt{a_{n-i}·a_{n+i}} \), n>i.
Amit úgy is fogalmazhatunk, hogy a mértani sorozat n-edik eleme (n>1) mértani közepe a tőle szimmetrikusan elhelyezkedő két másik tagnak.
Már az ókori egyiptomiak is ismerték a számtani és mértani sorozatot. Erről árulkodik az un. Rhind-papirusz, amely Kr.e. 1750 körül készült.
A fenti 2. példán láttuk, hogy a negyedik négyzet oldala: a4=a1⋅(√2)3.
Tehát azt kaptuk, hogy a negyedik négyzet oldala kifejezhető a sorozat első tagjának és a sorozat állandójának (q) segítségével. Ez általánosan is megfogalmazható:
A mértani sorozat n-edik tagjának meghatározása
A mértani sorozat n-edik tagja kifejezhető a sorozat első tagjának és a sorozat állandójának (q) segítségével a következő módon: an=a1⋅qn-1.
Bizonyítás:
Az állítás helyességét teljes indukcióval fogjuk belátni. Közben felhasználjuk a sorozat definícióját, miszerint: an=an-1⋅q.
1. A definíció felhasználásával belátjuk az állítást az első náhány konkrét n értékre:
a2=a1⋅q definíció szerint. a3=a2⋅q a definíció szerint, de felhasználva az a2-re kapott kifejezést: a3=a1⋅q2.
2. Indukciós feltevés: Feltételezzük, hogy n olyan index, amire még igaz: an=a1⋅qn-1. Ilyen az 1. pont szerint biztosan van.
3. Ezt felhasználva, bebizonyítjuk, hogy a rákövetkező tagra is igaz marad, azaz: an+1=a1qn. Tehát azt, hogy a tulajdonság öröklődik.
Definíció szerint az n-edik tag után következő tag: an+1=an⋅q.
Itt an helyére behelyettesítve az indukciós feltételt: an+1=(a1⋅qn-1)⋅q.
Egyszerűbben: an+1=a1qn.
Ezt akartuk bizonyítani.
A mértani sorozat tagjainak összege
Állítás:
Mértani sorozat első n tagjának összege: \( S_{n}=\frac{a_{1}·\left(q^n-1\right) }{q-1} \; q≠1 \).
Bizonyítás:
Írjuk fel az első n tag összegét tagonként:
Sn=a1+a2+a3+…+an-2+an-1+an.
Majd felhasználva az n-edik tagra fent bizonyított képletet:
1) Sn=a1+a1⋅q+a1⋅q2+…+a1⋅qn-3+a1⋅qn-2+a1⋅qn-1.
Szorozzuk végig q-val:
2) Sn⋅q=a1⋅q+a1⋅q2+a1⋅q3+…+a1⋅qn-2+a1⋅qn-1+a1⋅qn.
Vonjuk ki a 2) egyenlőségből az 1)-t. Ekkor az 1. egyenletből az első tag, a második egyenletből az utolsó tag kivételével minden tag kiesik. Így:
Sn⋅q- Sn=a1⋅qn-a1.
A baloldalon Sn-t, jobb oldalon a1-t kiemelve: Sn⋅(q-1)=a1⋅(qn-1).
Ezt (q-1)≠0-val osztva: \( S_{n}=\frac{a_{1}·\left(q^n-1\right) }{q-1} \; q≠1 \).
Ezt kellett bizonyítani.
Ha q=1, akkor a mértani sorozat állandó tagú, azaz minden k-ra ak=a1, k∈ℤ+. Ezért ebben az esetben Sn=n⋅a1.
Az i.e. 2000 tájáról származó egyiptomi Rhind-féle papiruszon fordul elő a következő feladat:
„7 ház mindegyikében 7 macska él. Mindegyik macska 7 egeret őriz. Hány egér volt összesen?”
Valószínű tehát, hogy az ókori egyiptomiak már ismerték a mértani sorozatot, annak összegképletét, persze nem a jelenlegi formájában.


Comments are closed, but trackbacks and pingbacks are open.