Bevezető feladat
Ábrázoljuk és jellemezzük korlátosság és monotonitás szempontjából az: \( a_{n}=\frac{n+1}{n-1} \) sorozatot!
Megoldás
A sorozat ábrázolása:
A sorozat első néhány eleme: a1=-nincs értelmezve; a2=3; a3=2; a4=5/3; a5=6/4; a6=7/5; a7=8/6≈1,33; a8=9/7≈1,29; a9=10/8; a10=11/9;…
A sorozat grafikonját a mellékelt animáció szemlélteti: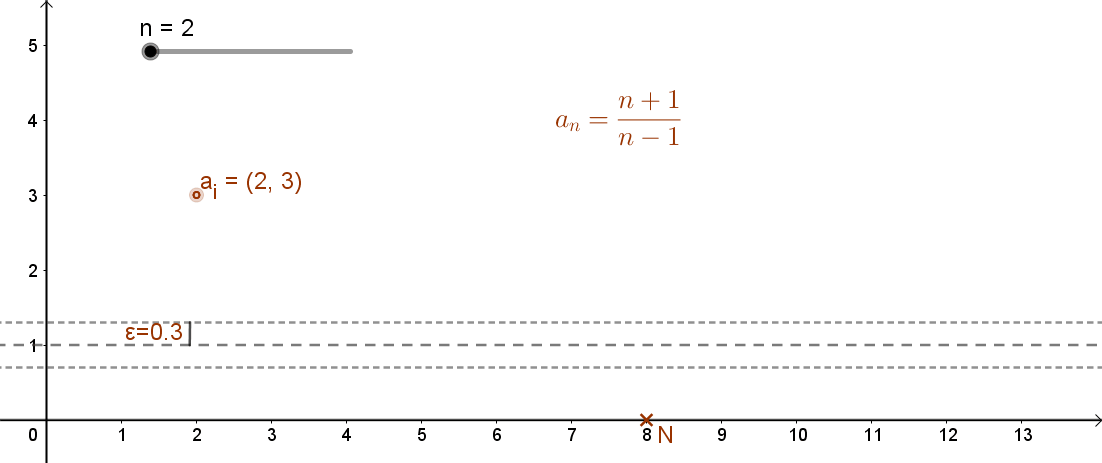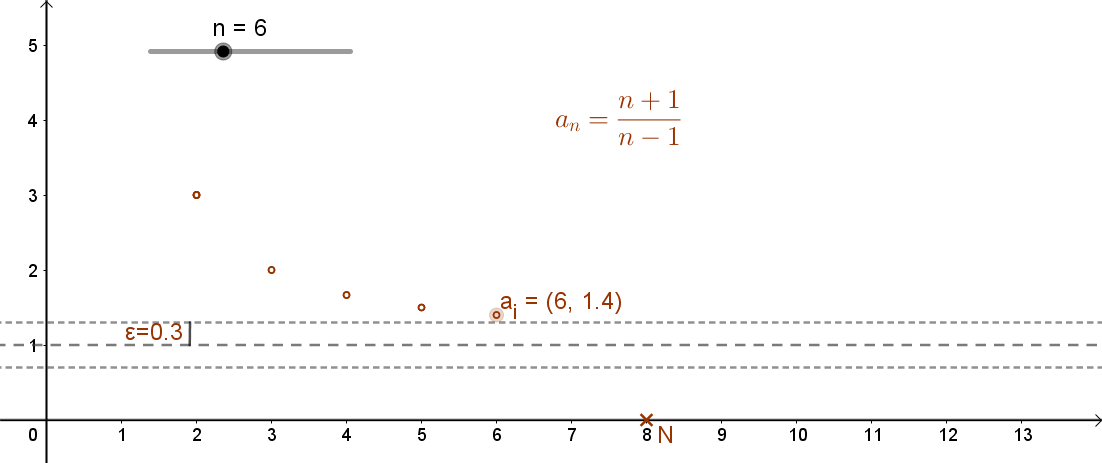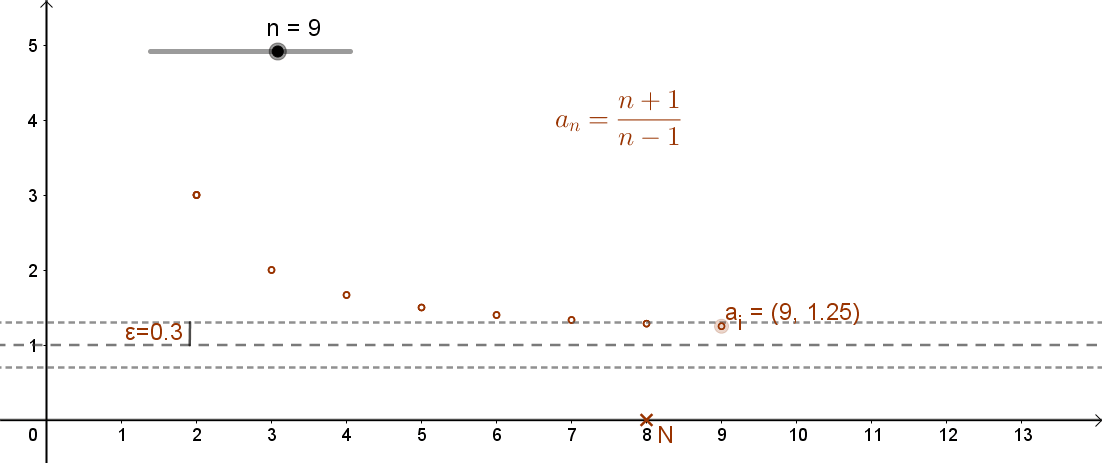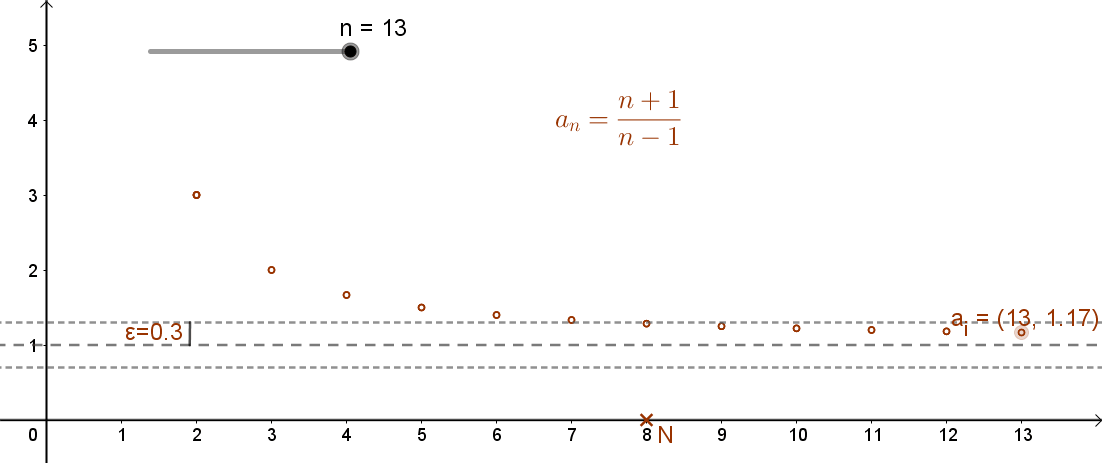
A sorozat jellemzése
Korlátosság: Mivel a sorozat számlálója mindig nagyobb, mint a nevező és mind a nevező mind a számláló pozitív, ezért biztosan állítható, hogy a sorozat minden tagja nagyobb, mint 1. Tehát alulról korlátos.
Menete: A sorozat első néhány tagja azt sugallja, hogy a sorozat szigorúan monoton csökken.
Ez természetesen algebrailag is igazolható: an>an+1.
Azaz: \( \left\{\frac{n+1}{n-1} \right\}>\left\{\frac{(n+1)+1}{(n+1)-1} \right\} \). A jobb oldali törtben persze elvégezzük az összevonást, akkor \( \left\{\frac{n+1}{n-1} \right\}>\frac{n+2}{n} \).
A nevezőkkel átszorozva kapjuk a következő egyenlőtlenséget: n⋅(n+1)>(n+2)⋅(n-1). (Itt tudjuk, hogy mindkét nevező pozitív, tehát a relációs jel nem változik.) Zárójelek felbontása után: n2+n>n2+n-2, azaz 0>-2 Ez pedig nyilvánvalóan igaz.
Így beláttuk, hogy az \( a_{n}=\left\{\frac{n+1}{n-1} \right\} \) sorozatban tetszőleges n-re a tagok egyre kisebbek lesznek vagyis minden tag nagyobb a rákövetkezőnél: an>an+1.
Ebből az következik, hogy a sorozat felülről is korlátos. Legnagyobb értékű eleme az első: a2=3.
Vegyük fel a következő 6 tized hosszúságú nyílt intervallumot: ]0,7; 1,3[. Az 1-es érték 0,3 távolságra van az intervallum két végpontjától.
Definíció:
Egy „A”valós szám ε>0 sugarú környezetén értjük azokat a valós számokat, amelyeknek az „A” számtól való távolsága kisebb, mint ε. Ez a ]A- ε ;A+ ε[ nyílt intervallum.
A fenti példa esetén tehát: ε=0,3.
A fenti sorozatnak lesz-e olyan tagja, amelyik már ebbe az intervallumba esik? És ha igen, milyen sorszámtól kezdődően? A sorozat 7. tagjának értéke: a7=8/6≈1,33, míg a 8. tag értéke a8=9/7≈1,29.
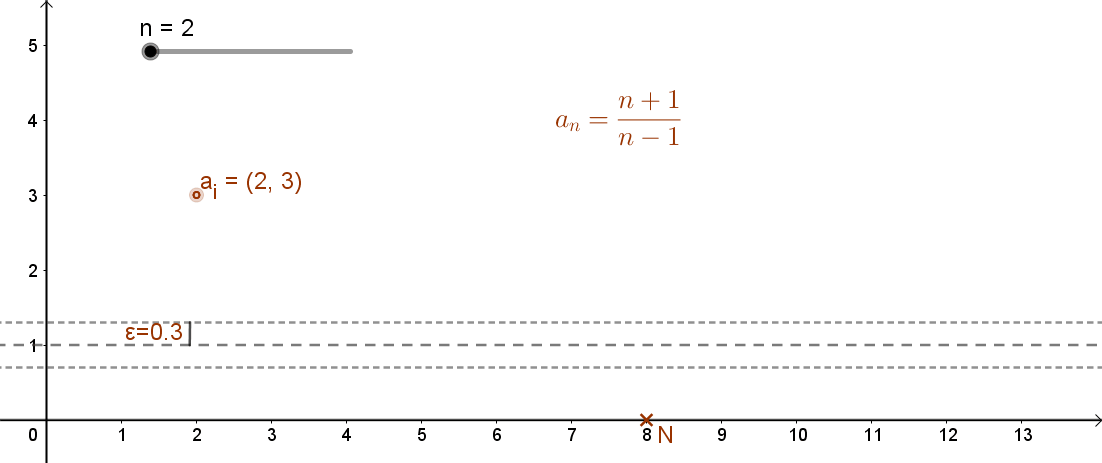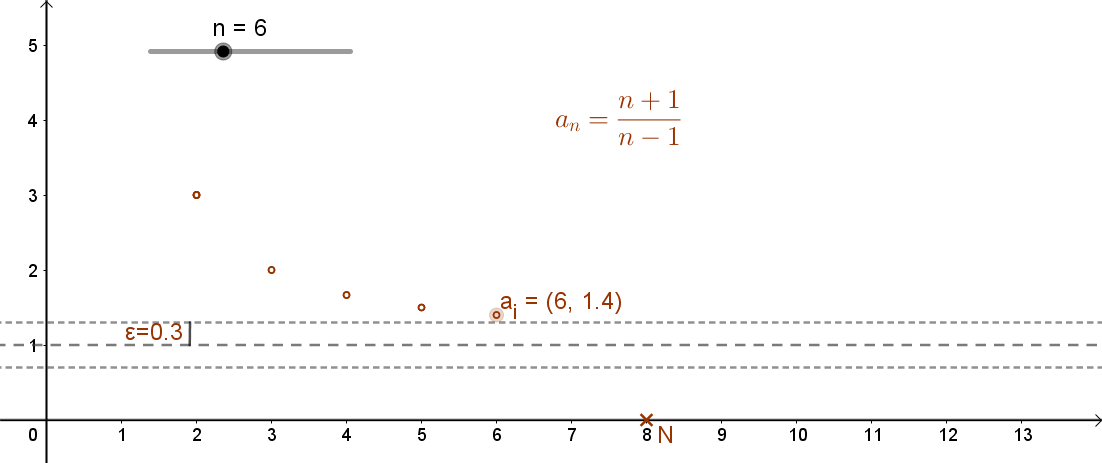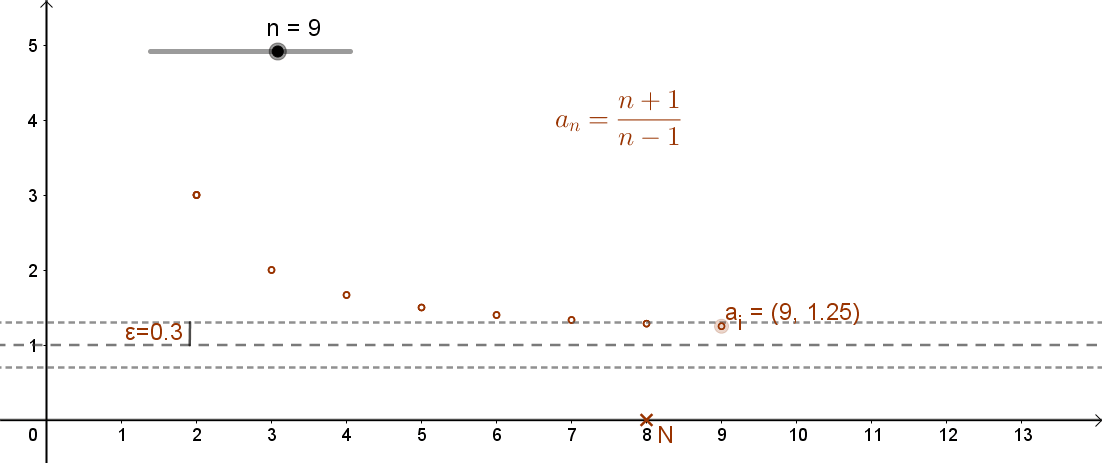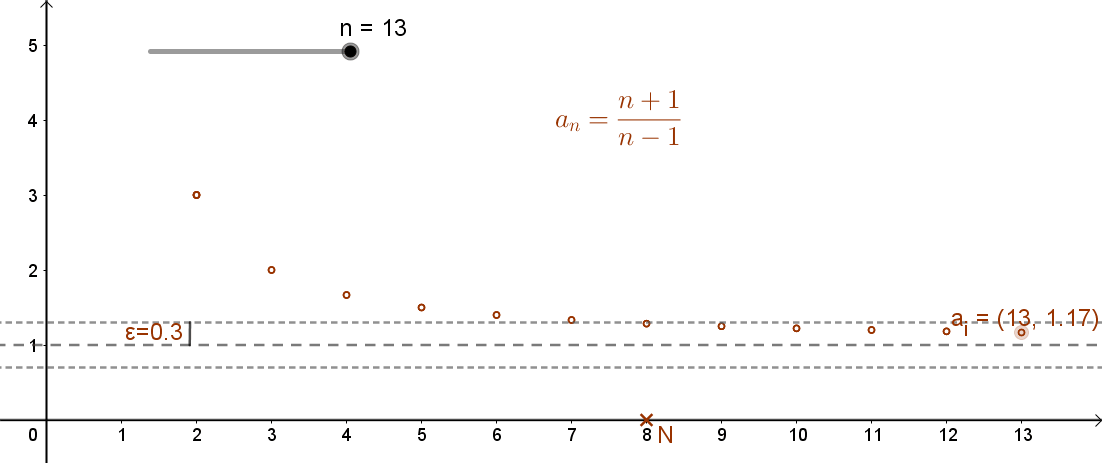
Tehát a sorozat 8. tagja már csak kb. 0,29 századnyira tér el az 1-től. Ugyanakkor a sorozat 100. tagjának értéke a100=101/99≈1,02. Ez már csak 0,02 századnyira tér el az 1-től.
Látható tehát, hogy a sorozat tagjai „egyre közelebb” kerülnek az 1-hez. Minél nagyobb sorszámú tagját nézzük a sorozatnak, a kapott érték egyre kisebb mértékben tér el az 1-től.
Vizsgáljuk most meg monotonitás és korlátosság szempontjából a következő sorozatot! bn=3+(-1/2)n
Először írjuk fel a sorozat első néhány elemét!
b1=3-1/2=5/2; b2=3+1/4=13/4; b3=3-1/8=23/8; b4=3+1/16=49/16; b5=3-1/32; b6=3+1/32; b7=3+1/32. .
Belátható, hogy a sorozat alulról is és felülről is korlátos. A sorozat legkisebb eleme a b1, a legnagyobb eleme a b2. Hiszen minden páratlan sorszámú elemnél egyre kisebb értéket levonunk 3-ból, míg minden páros sorszámú elem esetén egyre kisebb számot adunk hozzá a 3-hoz.
Azaz k=b1=5/2=2,5≤bn≤b2=3,25=49/16=K.
A fentiekből az is következik, hogy minden páratlan sorszámú tag kisebb, mint 3, minden páros sorszámú tagja pedig nagyobb, mint 3, ezért ez a sorozat sem nem növekvő, sem nem csökkenő.
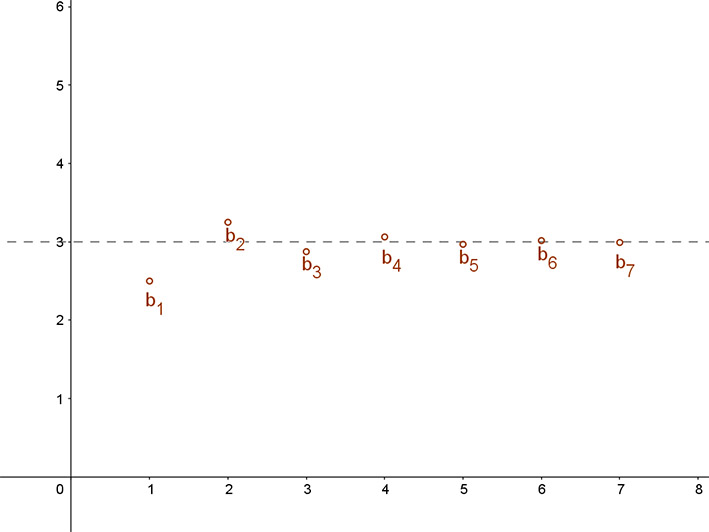 Az is látható, hogy a sorozatnak minél magasabb sorszámú tagjait nézzük, azok „egyre közelebb” kerülnek a 3-hoz. A páratlan indexűek egyre kisebb mértékben kisebbek, mint 3, a páros indexűek egyre kisebb mértékben nagyobbak, mint 3. De a 3-as szám nem tagja a sorozatnak.
Az is látható, hogy a sorozatnak minél magasabb sorszámú tagjait nézzük, azok „egyre közelebb” kerülnek a 3-hoz. A páratlan indexűek egyre kisebb mértékben kisebbek, mint 3, a páros indexűek egyre kisebb mértékben nagyobbak, mint 3. De a 3-as szám nem tagja a sorozatnak.
Természetesen ezt a „egyre közelebb” kifejezést pontosan definiálni kell.
Határérték fogalma
Definíció:
Az „A számot az {an} sorozat határértékének nevezzük, ha bármely ε>0 számhoz (távolsághoz) található olyan N szám (küszöbindex) , hogy ha n>N, akkor |an-A|<ε (Cauchy –féle definíció).
Nézzük ezt az első példán. Azt sejtjük, hogy a sorozat egyre közelebb kerül az 1-hez, azaz a fent definíció szerint a sorozat határértéke az 1, vagyis A=1. Megadtunk az 1 környezetének egy 0,3 sugarú intervallumát, azaz ε=0,3. Ha a sorozat 8. indexű tagját néztük, akkor |a8-1|=|1,29-1|=0,29<0,3.
Az is könnyen belátható, hogy ha az A=1 számnak az 0,3-nál kisebb sugarú környezetét nézzük, akkor is lesz a sorozatnak – ugyan egy magasabb indexű – tagja, amelynek az eltérése az A=1 határértéktől még ettől az értéknél is kisebb. Azaz az környezet mértéke és a küszöbindex értéke egymástól függ. Kisebb ε–hoz nagyobb küszöbindex tartozik és fordítva.
Az is megállapítható, hogy a fenti sorozatok esetén, hogy csak véges számú tag esik az adott környezeten kívül, míg fenti sorozatoknak (a küszöbindextől kezdődően) végtelen sok tagja ebbe a környezetbe fog beleesni.
Megfogalmazható tehát a határérték fogalma másképp is:
Definíció:
Az an sorozatnak létezik határértéke, ha van olyan A szám, hogy az A szám tetszőleges sugarú környezetébe a sorozat végtelen sok tagja esik és csak véges sok tagja marad ki belőle. Jelölések: an→A, illetve \( \lim_{n \to \infty }a_{n}=A \.
A fenti példák esetén: \( a_{n}=\left\{\frac{n+1}{n-1} \right\} \) →1 és bn=3+(-1/2)n→3. Illetve \( \lim_{ n \to \infty }\frac{n+1}{n-1}=1 \) és \( \lim_{n \to \infty }=3+\left(-\frac{1}{2}\right)^n=3 \).
Az olyan sorozatokat, amelyeknek van határértéke konvergens (összetartó) sorozatoknak, amelyeknek pedig nincs, azokat divergens (széttartó) sorozatoknak nevezzük.
Konvergens sorozatok határértéke monoton növekvő sorozat esetén a sorozat felső határa (suprémuma), monoton csökkenő sorozatok esetén a sorozat az alsó határa (infimuma). (Supremum: a legkisebb felső korlát; infimum: a legnagyobb alsó korlát).
A {(-1)n} sorozatnak nincs határértéke. Minden páros indexű tagja =1; minden páratlan indexű tagja =-1. Mind a +1; mind a -1 „környezetében” végtelen sok (azonos értékű) tagja van a sorozatnak. Bár ennek a sorozatnak a +1 és a -1 számok tetszőleges kicsi környezetében is végtelen sok elem van, de végtelen sok elem marad ki akár a +1 és akár a -1 tetszőleges kicsi környezetéből. Ezért ennek a sorozatnak a +1 és a -1 pontok torlódási pontjai (torlódási helyek).
Definíció:
A „t” szám a sorozat torlódási pontja (torlódási helye), ha „t” bármilyen kis környezete a sorozat végtelen sok elemét tartalmazza.
Tétel:
Egy konvergens sorozatnak csak egy torlódási pontja lehet.
A cn = 2 (konstans) sorozat konvergens, hiszen miden tagja =2, tehát a 2 bármilyen kicsi sugarú környezetébe esik a sorozat minden tagja és a határérték is = 2.
Ha egy korlátos sorozatnak egyetlen torlódási pontja van, akkor azt a torlódási pontot határértéknek nevezzük.
A definícióban ugyanazt fogalmaztuk meg, amit a bevezető elnevezésben: a konvergenciához korlátosság és egyetlen torlódási pont létezése szükséges.
(-1)n-ediken sorozatnak két torlódási pontja van: 1, ha n páros és -1, ha n páratlan.
Bolzano–Weierstrass tétel:
Korlátos sorozatnak mindig van legalább egy torlódási pontja.
A bizonyítás alapgondolata:
Ha az (an ) korlátos, akkor minden eleme két korlát, a ka és a Kf között található.
A két korlát által meghatározott intervallumot megfelezzük és azt a részt, amelyben a sorozatnak végtelen sok eleme van, újra felezzük és így tovább. A felezgetést (elvileg) „végtelenszer” megismételjük, ekkor a végtelen sok elemet tartalmazó intervallum ponttá zsugorodik, ez a torlódási pont.
A Fibonacci sorozat nyilván felülről nem korlátos, de szigorúan monoton nő. Bármilyen nagy valós számnál is lesz nagyobb értékű tagja a sorozatnak Az ilyen típusú sorozatok ugyan divergensek, de azt mondjuk, hogy tart a végtelenhez. A felülről nem korlátos monoton sorozatok a +∞-hez, az alulról nem korlátos és monoton csökkenő sorozatok pedig a -∞-hez tartanak (közelítenek).
Definíció:
Az {an} sorozat tart a végtelenhez (∞–hez), ha minden K számhoz létezik olyan N szám, hogy ha n > N, akkor an > K, illetve an < K (Az an sorozat a végtelenhez divergál.)
Ezt így jelöljük: \( \lim_{ n \to \infty }=+∞ \)illetve \( \lim_{ n \to \infty }=-∞ \).


Comments are closed, but trackbacks and pingbacks are open.