Számsorozatok jellemzése

A számsorozatok a pozitív  természetes számokon értelmezett függvény.

Bár függvényként kezelhetjük őket, de a definíció következtében a függvényvizsgálatok egy részére nincs szükség. Hiszen például az értelmezési tartomány adott, a pozitív természetes számok halmaza. Persze bizonyos sorozatoknál ez szükülhet is. (pl: az a_n= 1/(n-3) esetén n≠3.)
Nincs értelme például a folytonosság tulajdonságáról sem beszélni, hiszen a számsorozat változói természetes számok,  amelyek diszkrét értékek.

A számsorozatok esetén a két legfontosabb vizsgálati szempont a korlátosság és a monotonitás.

Számsorozatok korlátossága:

Tekintük a következő sorozatot: ​​\( a_{n}=\left\{\frac{n+1}{n-1} \right\} \; n∈\mathbb{N}^{+} \; n>1 \)​.

Erről könnyen megállapítható, hogy minden tagja nagyobb lesz mint 1, hiszen a számlálója nagyobb, mint a nevezője. Az is rögtön kimondható, hogy a sorozat tagjai mind pozitív számok.

Alakítsuk át a sorozat hozzárendelési szabályát: ​\( a_{n}=\left\{\frac{n+1}{n-1} \right\}=\left\{ 1+\frac{2}{n-1}\right\} \; n∈\mathbb{N}^{+} \; n>1 \)​. Megállapítható, hogy a sorozat egyetlen egy tagja sem lehet nagyobb, mint 3, hiszen a 2/(n-1) tört értéke n=2 esetén 2, így a₂=(2+1)/(2-1)=3,  minden más n>2 esetén a sorozat tagjai  3-nal kisebbek lesznek.

A függvények korlátosságához hasonlóan definiálhatjuk a számsorozatok korlátosságát.

Definíció:

Az {a_n} sorozat felülről korlátos, ha van olyan „K” szám, hogy a sorozat minden a_n tagjára a_n ≤K teljesül. A „K” számot a sorozat felső korlátjának nevezzük.
Ha egy számsorozat felülről korlátos, akkor végtelen sok felső korlátja van.
A felülről korlátos sorozatok legkisebb felső korlátját a sorozat felső határának (szuprémumának) nevezzük.

Definíció:

Az {a_n} sorozat alulról korlátos, ha van olyan „k” szám, hogy a sorozat minden „a_n” tagjára a_n ≥ k teljesül. A „k” számot a sorozat alsó korlátjának nevezzük.
Ha egy számsorozat alulról korlátos, akkor végtelen sok alsó korlátja van.
Az alulról korlátos sorozat legnagyobb alsó korlátját a sorozat alsó határának (infimumának) nevezzük.

Definíció:

Az {a_n} sorozat korlátos, ha felülről és alulról is korlátos, azaz ha van olyan „k” és „K” szám, amelyre k ≤ a_n ≤ K teljesül.

Mondhatjuk, hogy a fenti sorozat korlátos, hiszen van alsó korlátja (k=1) és van felső korlátja is, K=3. Azaz 1<a_n ≤ 3

Legyen adott az b_n=(-2)ⁿ sorozat. Tagjai: b₁=-2; b₂=4; b₃=-8; b₄=16;…
A sorozat tagjai váltakozó előjelüek. Ez a sorozat nem korlátos, sem alulról, sem felülről.

Számsorozatok monotonitása:

Vizsgáljuk meg monotonitás szempontjából is a fenti \( a_{n}=\left\{\frac{n+1}{n-1} \right\} \)​ sorozatot. Számítsuk ki ennek a sorozatnak első néhány tagját:

a₂=3; a₃=2; a₄=5/3; a₅=6/4;…és így tovább. Ebből az a sejtésünk, hogy a tagok egyre kisebbek lesznek. Ez azonban csak sejtés. Ennek igazolásához meg kell oldani a következő egyenlőtlenséget: a_n>a_n+1.

Azaz: ​\( \left\{\frac{n+1}{n-1} \right\}>\left\{\frac{(n+1)+1}{(n+1)-1} \right\} \)​. A jobb oldali törtben persze elvégezzük az összevonást, akkor ​\( \left\{\frac{n+1}{n-1} \right\}>\frac{n+2}{n} \)​.

A nevezőkkel átszorozva kapjuk a következő egyenlőtlenséget: n⋅(n+1)>(n+2)⋅(n-1). (Itt tudjuk, hogy mindkét nevező pozitív, tehát a relációs jel nem változik.) Zárójelek felbontása után: n²+n>n²+n-2, azaz 0>-2 Ez pedig nyilvánvalóan igaz.

Így beláttuk, hogy az  \( a_{n}=\left\{\frac{n+1}{n-1} \right\} \)​ sorozatban tetszőleges n-re a tagok egyre kisebbek lesznek vagyis minden tag nagyobb a rákövetkezőnél: a_n>a_n+1.

Megjegyzés: Általában is elmondható, hogy a sorozatok monotonításának vizsgálatához egyenlőtlenség megoldására van/lehet szükség.

A függvények monotonitásához hasonlóan definiálhatjuk a számsorozatok monotonitását.

Definíciók:

Az {a_n} sorozat szigorúan monoton fogyó, ha minden „n”-re a_n> a_n+1.
(Azaz az egyenlőség nem fordul elő.)

Az {a_n} sorozat monoton fogyó, ha minden „n”-re a_n≥ a_n+1.
(Azaz az egyenlőség is előfordulhat.)

Az {a_n} sorozat szigorúan monoton növekvő, ha minden „n”-re a_n< a_n+1.
(Azaz az egyenlőség nem fordul elő.)

Az {a_n} sorozat monoton növekvő, ha minden „n”-re a_n≤ a_n+1.
(Azaz az egyenlőség is előfordulhat.)

Példák:

Nézzük a következő sorozatot: f₁=1; f₂=1; f_n=f_n-1+ f_n-2.
Azaz: 1; 1; 2; 3; 5; 8; 13;… és így tovább. (Ez az un. Fibonacci sorozat.)
Ábrázoljuk ezt a koordináta rendszerben:

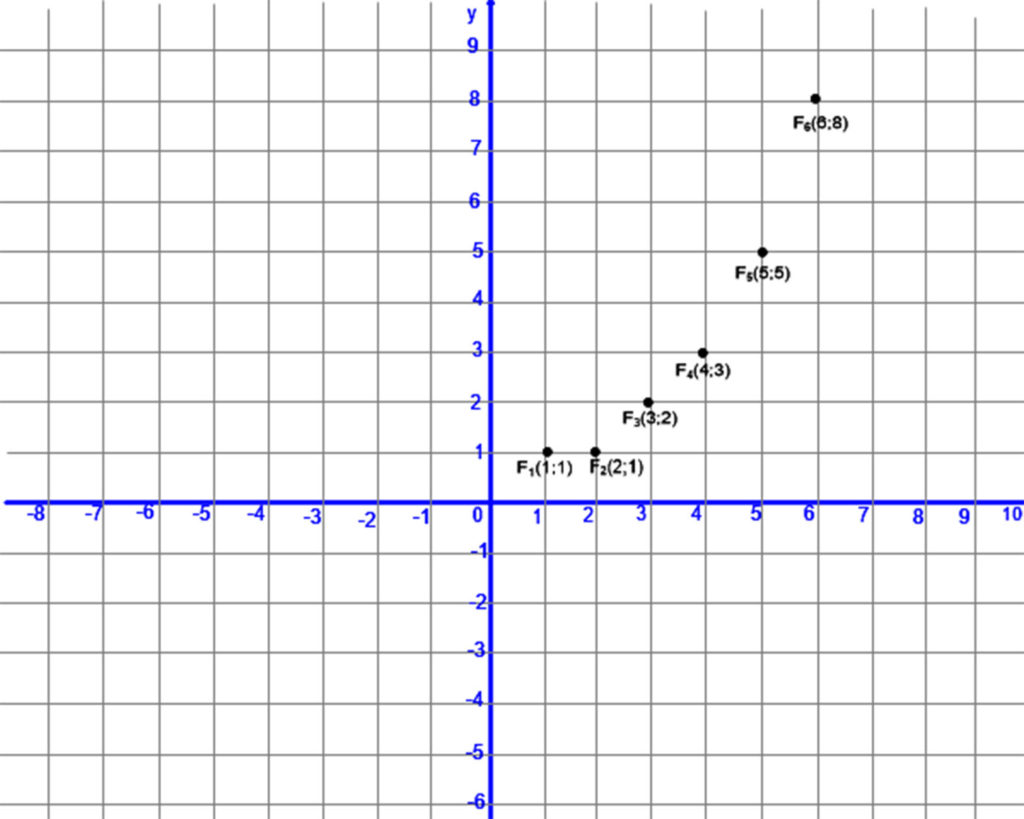
A sorozat definíciójából következik, hogy a 2. tagtól kezdve minden tag kisebb, mint a rákövetkező. Azaz: f_n< f_n+1, ha n>1. Tehát a Fibonacci sorozat monoton növekvő.

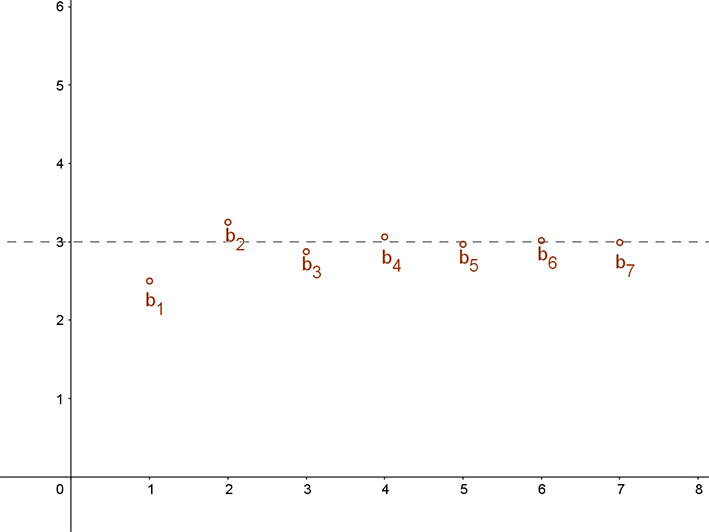
Vizsgáljuk most meg monotonitás szempontjából a következő sorozatot! ​\( b_{n}=3+\left( -\frac{1}{2}\right)^n \)​.
Először írjuk fel a sorozat első néhány elemét!
b₁=5/2, b₂=13/4, b₃=23/8, b₄=49/16,… és így tovább.
A definícióból következik, hogy minden páratlan sorszámú tag kisebb, mint 3, minden páros sorszámú tagja pedig nagyobb, mint 3, ezért ez a sorozat sem nem növekvő, sem nem csökkenő.

Érdemes megtekinteni az alábbi videót!