Aranymetszés, mint speciális arányt, szokták úgy is emlegetni, hogy „divina proportione”, azaz az „isteni arány”.
Definíció:
Aranymetszésről beszélünk, amikor egy mennyiséget, illetve egy adott szakaszt úgy osztunk két részre, hogy a kisebbik rész úgy aránylik a nagyobbikhoz, mint a nagyobbik rész az egészhez.
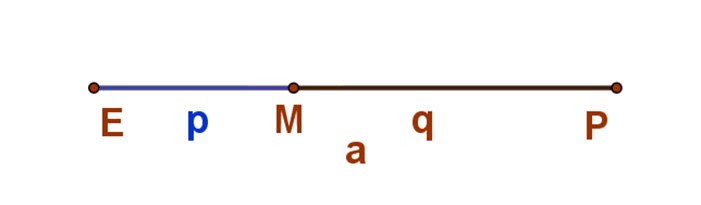
Rajz és formula: Aránypárral: p:q=q:(p+q)
Zeising német esztéta az 1800-as évek közepén az aranymetszésben vélte megtalálni az emberi test szépségének az okát, sőt a természeti tárgyak, élőlények és művészeti alkotások uralkodó morfológiai elvét. (morfológia: alaktan) Zeising természetesen túlzott.
A belvederei Apollón szobron sokan felfedezni vélik az aranymetszési arányt. Ez a szobor Kr. e. 350 körül készült.
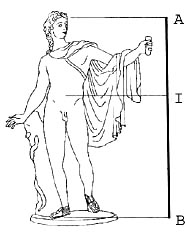
„Úgy tűnik„, az „I” -vel jelölt vonal az egész testet az aranymetszés arányának megfelelően osztja fel, azaz: AI:IB=IB:AB.
Az aranymetszés szerkesztése a szelő tételen alapszik.
Most azt fogjuk bizonyítani, hogy az így kapott M pont valóban a kívánt arányban osztja két részre az a=EP szakaszt.
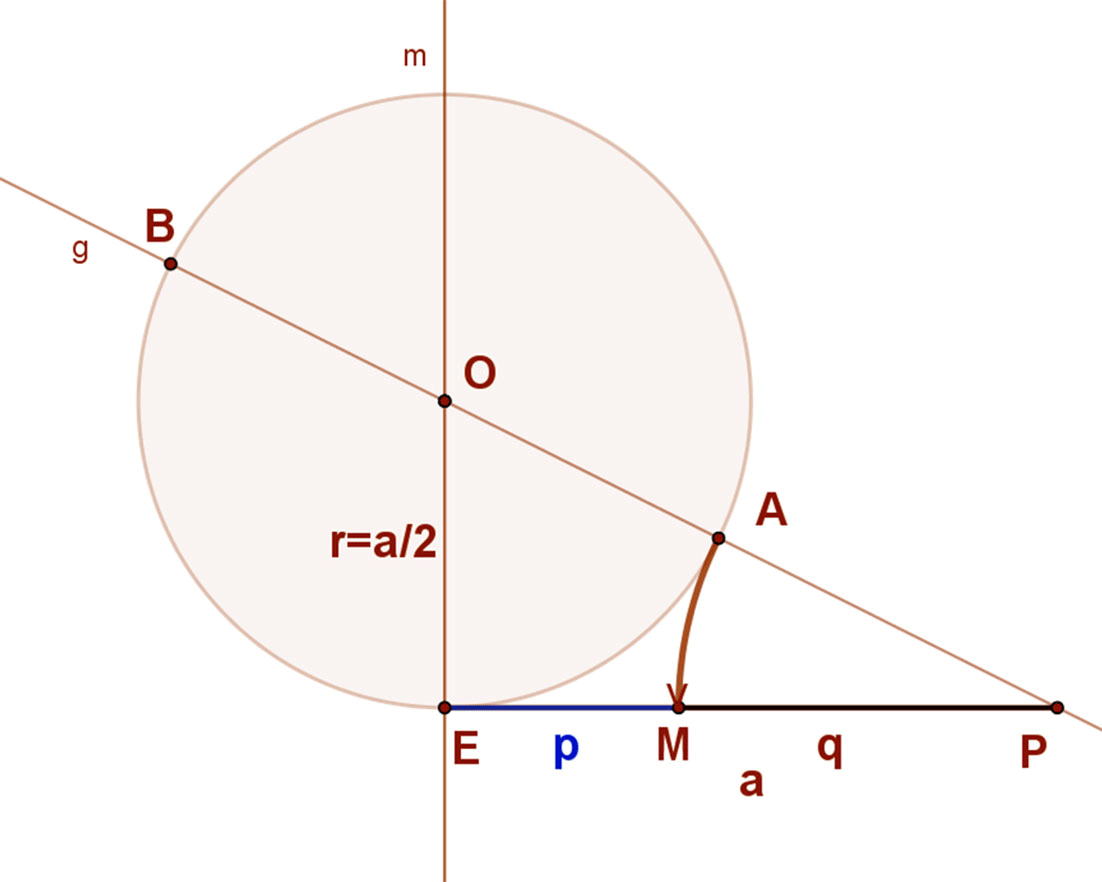A szelő és érintőszakaszok tétele tétele szerint PE2=PA*PB.
Vezessük be az ábra szerinti jelöléseket: EM=p, MP=q, EP=a
A szerkesztésből következik, hogy AP=MP=q, AB=a, és PB=a+q.
A szelő tételt ezekkel a jelölésekkel átírva: a2=q⋅(a+q).
Az egyenlőség jobb oldalán felbontva a zárójelet: a2=aq+q2.
Az aq tagot a bal oldalra átvíve: a2-aq=q2.
Itt a-t kiemelve: a(a-q)=q2.
Mivel a-q=p, ezért: ap=q2.
Az a=p+q jelölést is felhasználva: (p+q)p= q2.
Ezt aránypárba átírva: p:q=q:(p+q).
Tehát az M pont valóban az aranymetszésnek megfelelő arányban osztotta fel a PE=a szakaszt.
Az aranymetszési állandó.
A fenti arányból ki lehet számítani az aranymetszési állandót.
Azt, hogy hányad része a nagyobbik (q) szakasz az egésznek.
Felhasználva, hogy p=a-q és p+q=a, írjuk fel még egyszer az aranymetszési arányt úgy, hogy a p változó ne szerepeljen benne: (a-q):q=q:a.
Ezt szorzat alakba írva: q2=a⋅(a-q), vagyis q2=a2-aq. (Lásd fenti levezetés 3. sora.) Ezt q-ra, mint ismeretlenre rendezve (és a-t paraméternek tekintve):
q2+aq-a2=0. Ami q-ban másodfokú egyenlet.
Ezt a megoldóképlettel megoldva: \( q=a·\frac{\sqrt{5}-1}{2} \) adódik, ami azt jelenti, hogy az aranymetszés hosszabbik (q) szelete \( \frac{\sqrt{5}-1}{2} \)≈ 0,618034-szerese az eredeti „a” szakasznak. Azaz \( \frac{q}{a}=\frac{\sqrt{5}-1}{2} \).
Ezt és a definíciót felhasználva felhasználva kapjuk, hogy az aranymetszés hosszabbik és rövidebbik szeletének az aránya: \( \frac{\sqrt{5}+1}{2} \)≈ 1,618034.
Hiszen a definíció szerint: \( \frac{p}{q}=\frac{q}{a} \). Ennek reciprokát véve és az előző értéket felhasználva:
\[ \frac{q}{p}=\frac{a}{q}= \frac{2}{\sqrt{5}-1}=\frac{\sqrt{5}+1}{2} \]
Tehát a az aranymetszés hosszabbik és rövidebbik szakaszának az aránya: \( \frac{\sqrt{5}+1}{2}≈1,618034. \)
Ezt az állandót a görög ABC nagy „F” betűjével, Φ-vel jelöljük. Φ=\( \frac{\sqrt{5}+1}{2} \)
Alkalmazása:
Aranymetszéssel lehet szabályos öt- és tízszöget szerkeszteni.
Az r sugarú körbe írt szabályos 10 szög oldala a kör sugarának aranymetszéssel kapott hosszabbik szelete. Szabályos 10 szögből természetesen könnyű szabályos ötszöget szerkeszteni.
A szabályos ötszög átlói az aranymetszésnek megfelelő arányban metszik egymást, és az átlók a pentagramot, azaz a Pitagorasz csillagot határolják körül.
A Fibonacci sorozat egyre nagyobb sorszámú elemeinek hányadosa egy állandó számhoz, az aranymetszéssel kapott hosszabbik szakasznak a rövidebbikhez való arányához azaz a Φ=\( \frac{\sqrt{5}+1}{2} \)≈1.618-hoz közelít.
A logaritmikus spirál is kapcsolatban van az aranymetszéssel. A logaritmikus spirál olyan alakzat, ahol a spirál vonal két egymást követő íve között a távolság egyre növekszik úgy, hogy a növekedés arányos az elfordulás szögével. Ilyet figyelhetünk meg például egyes csigák mészháza esetén is.
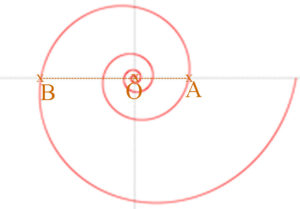
Megmutatható, hogy a logaritmikus spirál középpontján áthaladó egyenes a spirálkarokat az aranymetszési aránynak megfelelően metszi.
A mellékelt ábra esetében: OA : OB = OB : AB.
Ez szorzat alakban: OB2 = OA⋅AB.
Egyes galaxisok karjai gyakran logaritmikus spirál alakúak
Jacob Bernoulli azt kívánta, hogy síremlékére a logaritmikus spirált véssék.
Comments are closed, but trackbacks and pingbacks are open.