Háromszög súlyvonalai egy pontban metszik egymást

Mi is a háromszög súlyvonala?

Definíció:

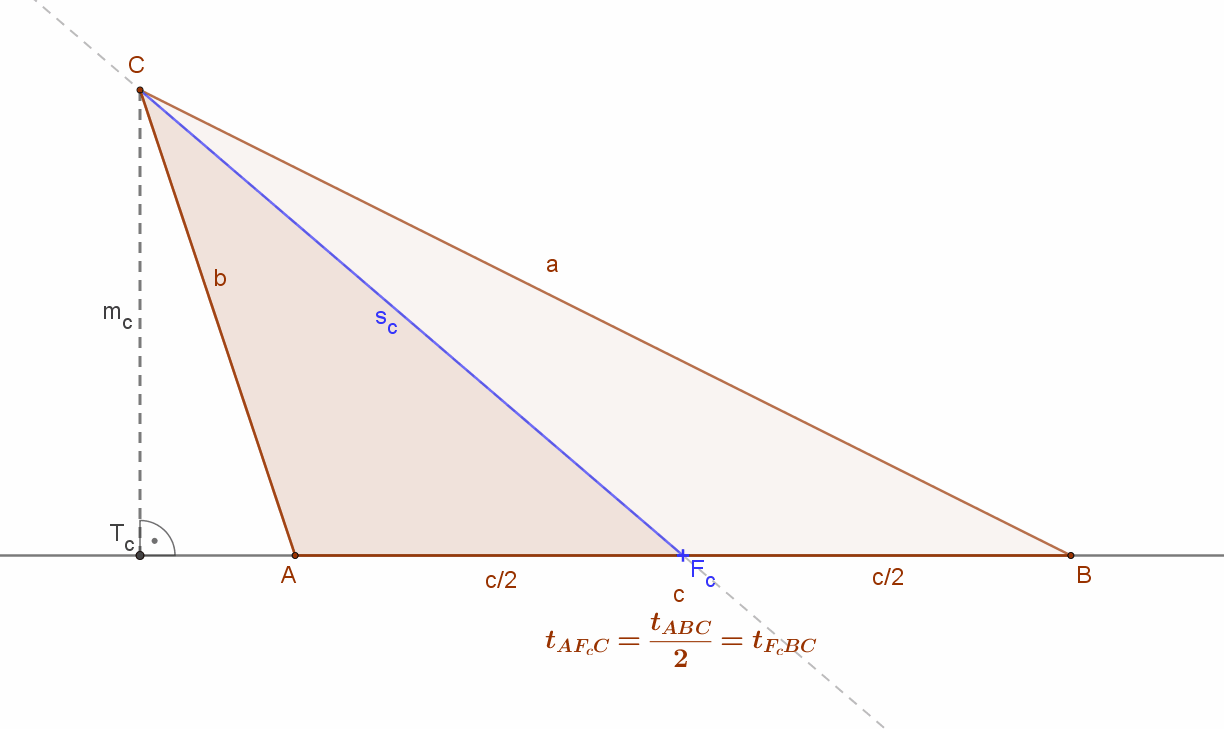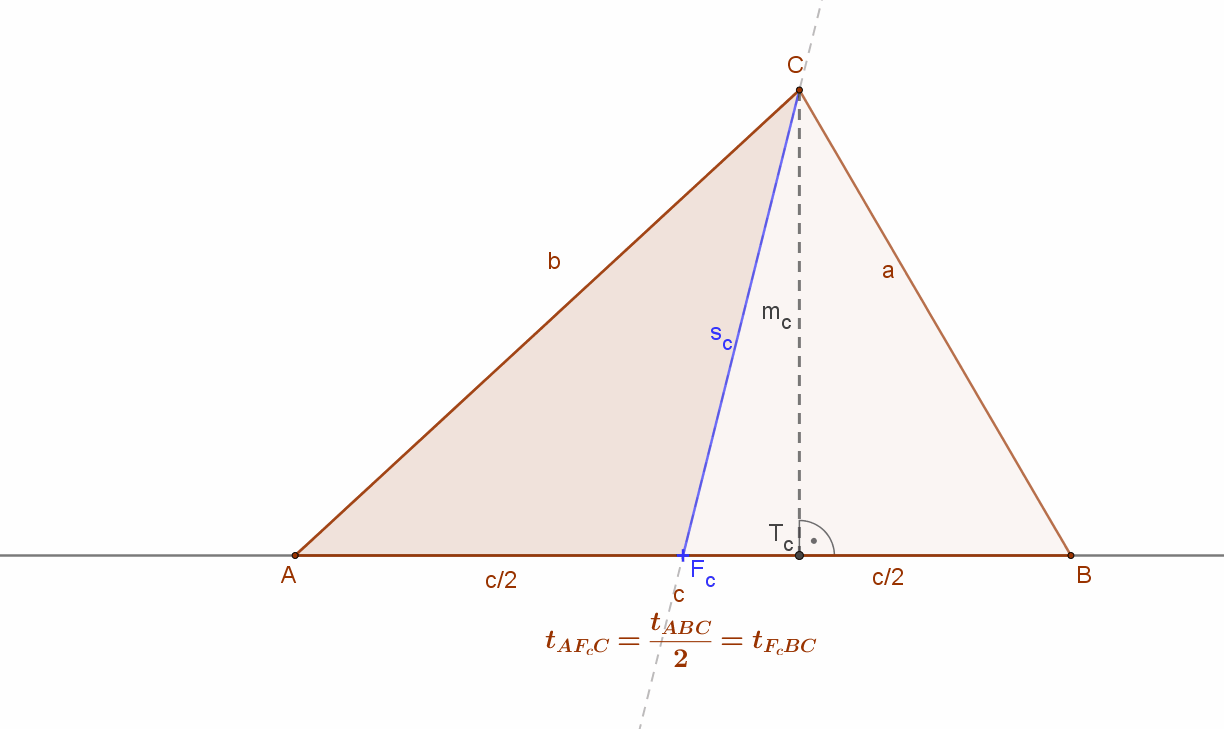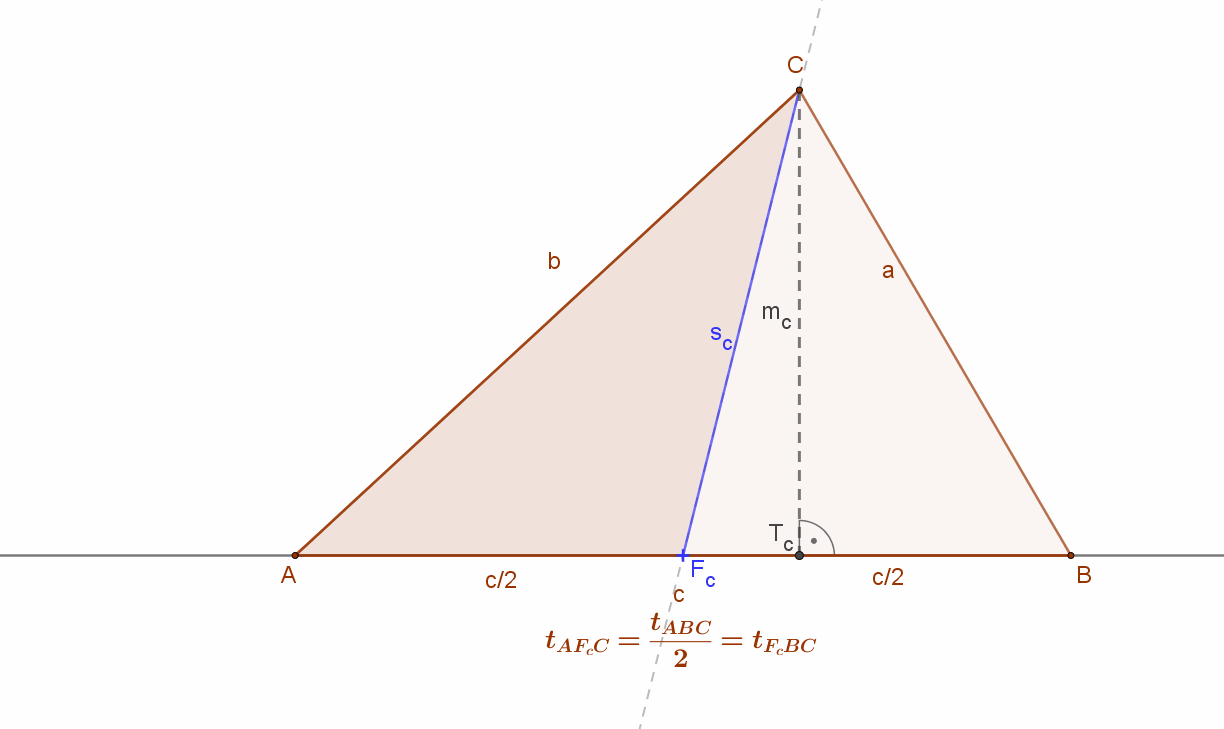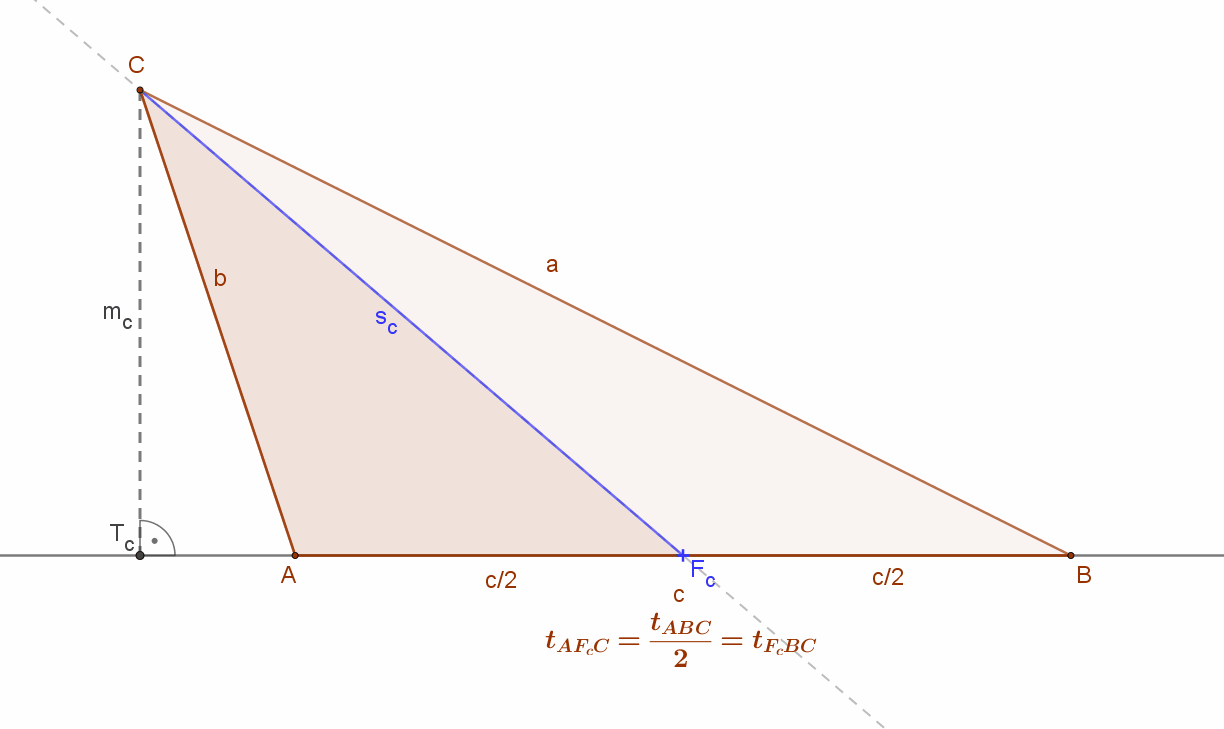
Egy háromszög súlyvonala a háromszög egy adott csúcsát és a szemközti oldal felező pontját összekötő vonal (illetve szakasz).

A súlyvonalról néhány ismeret:

• Egy háromszögnek értelemszerűen három súlyvonala van. Ezek minden esetben a háromszög belsejében haladnak.
• Súlyvonal általában nem merőleges a szemközti oldalra. Kivéve, ha a háromszögnek a súlyvonalat közrefogó oldalai egyenlő hosszúak.
• A háromszög súlyvonala felezi a háromszög területét. Másképpen mondva, a súlyvonal két egyenlő területű háromszögre vágja az eredeti háromszöget. Hiszen a súlyvonal felezi a szemközti oldalt és a két rész-háromszögnek megegyezik a szemközti oldalhoz tartozó magassága.
• Ha egy homogén anyagból készített háromszöget egyik súlyvonalára fektetve vízszintesen támasztunk alá, akkor a háromszög egyensúlyi helyzetben marad. Innen az elnevezés.

Állítás: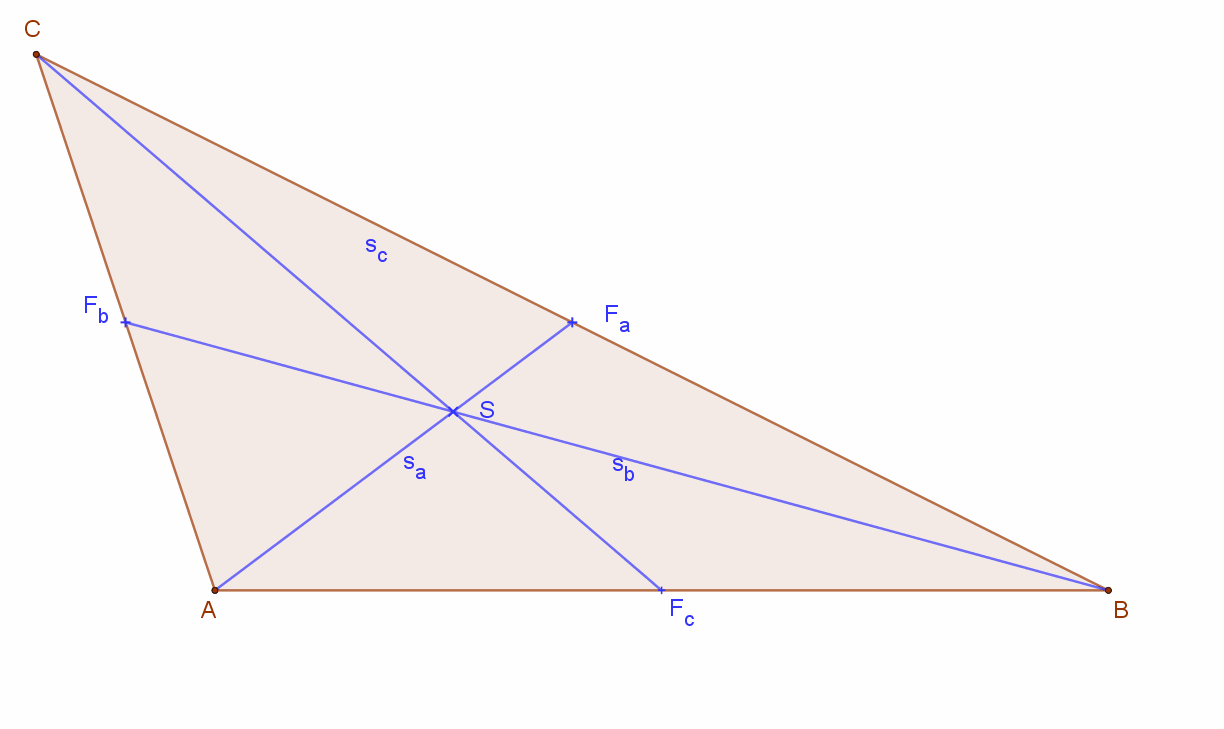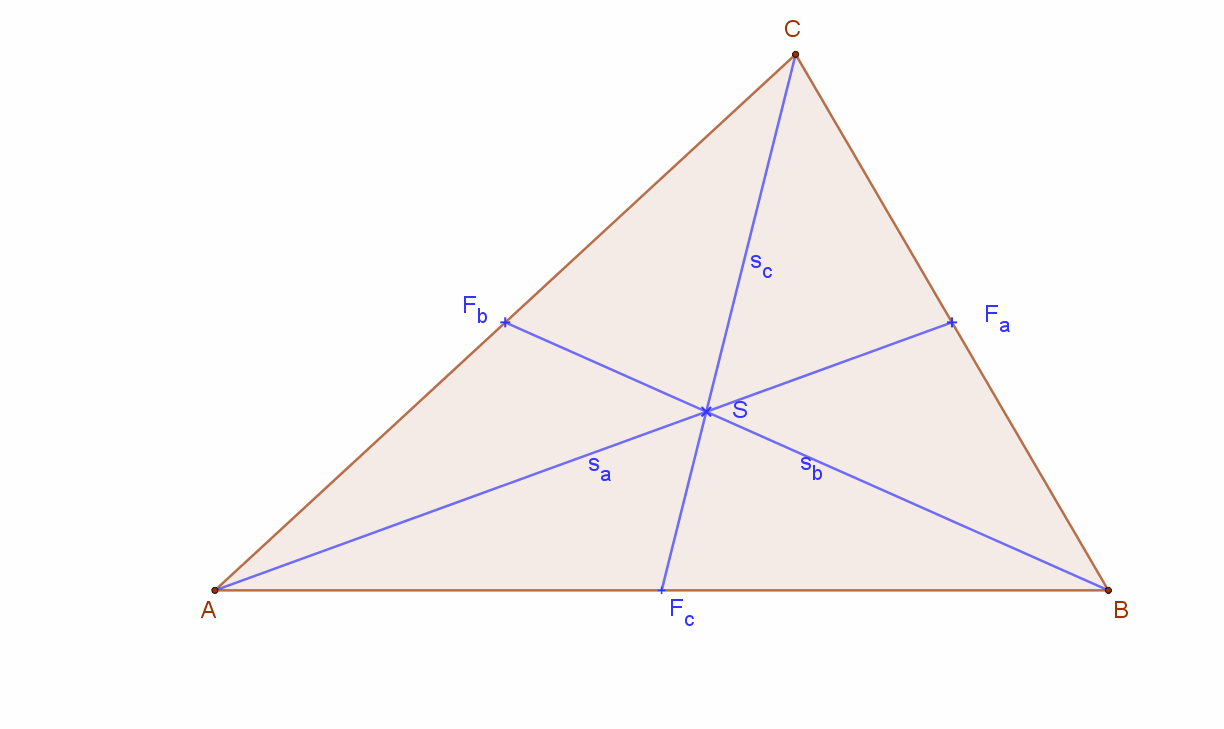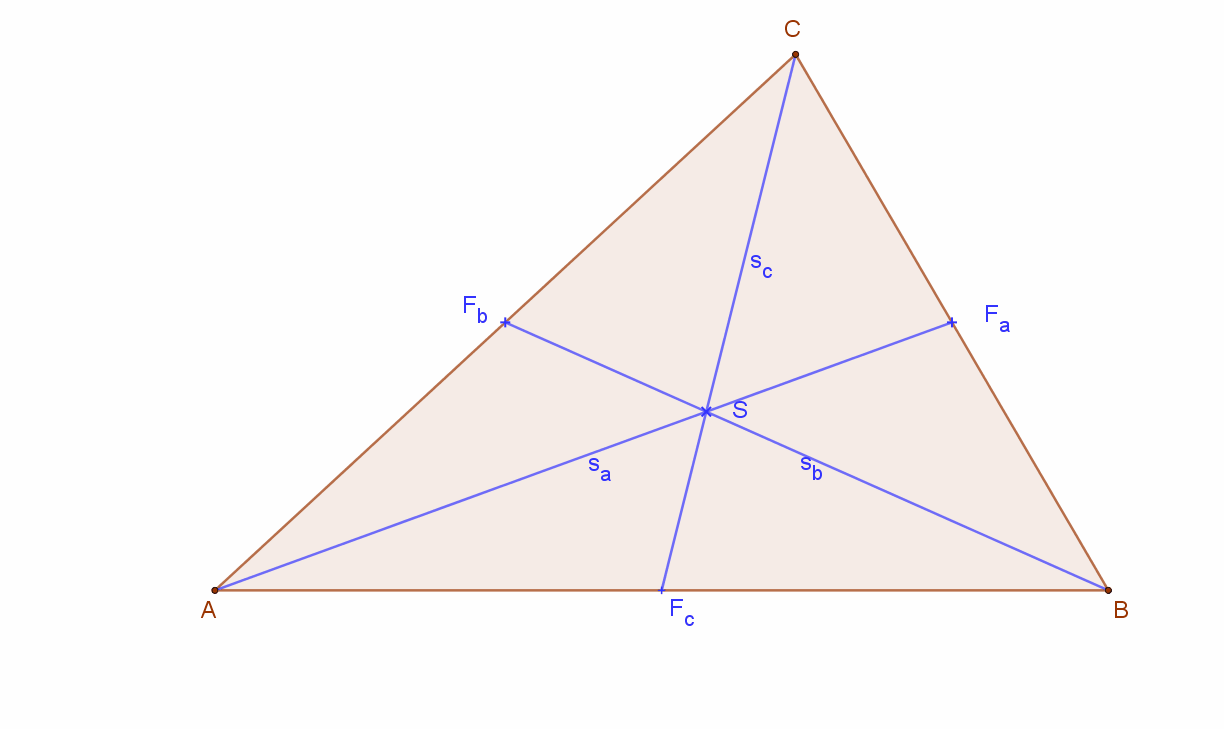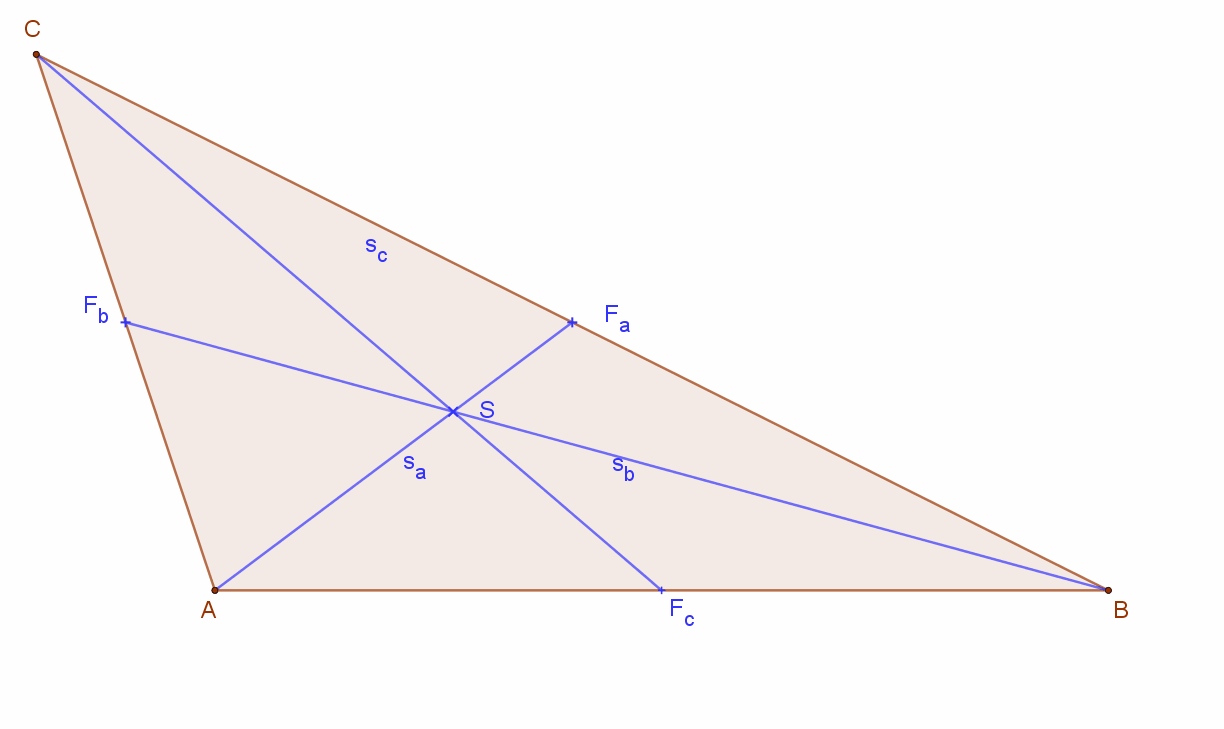

A háromszög súlyvonalai egy pontban, a súlypontban metszik egymást. A súlypont a súlyvonalakat 2:1 arányban osztja két részre úgy, hogy a hosszabb szakasz a csúcs felől van. Azaz: AS:SF_a=BS:SF_b=CS:SF_c=”2:1″

Bizonyítás:

Húzzuk meg az A és a B csúcsból induló súlyvonalakat. Ezeknek a szemközti oldalon lévő metszéspontját jelöljük F_a ill. F_b betűvel. A két súlyvonal metszéspontja S.

1. F_bF_a szakasz az ABC háromszög középvonala, ezért F_bF_a párhuzamos AB-vel, és F_bF_a=AB/2.
2. Az ABS háromszög hasonló F_bF_aS háromszöghöz, mert szögeik egyenlők. Hiszen egyrészt ASB ∠ =F_aSF_b ∠ (csúcsszögek), másrészt ABS∠ =SF_bF_a∠ (váltószögek).
3. Mivel F_bF_a=AB/2, ezért ASB és F_aSF_b háromszögek hasonlósági aránya 2:1.
Így AS:SF_a=2:1, és BS:SF_b=2:1. Ezt akartuk bizonyítani.

Mivel a bizonyításnál két tetszőleges súlyvonalra láttuk be az állítást, ezért ez a harmadik súlyvonalra is igaz.

Feladat: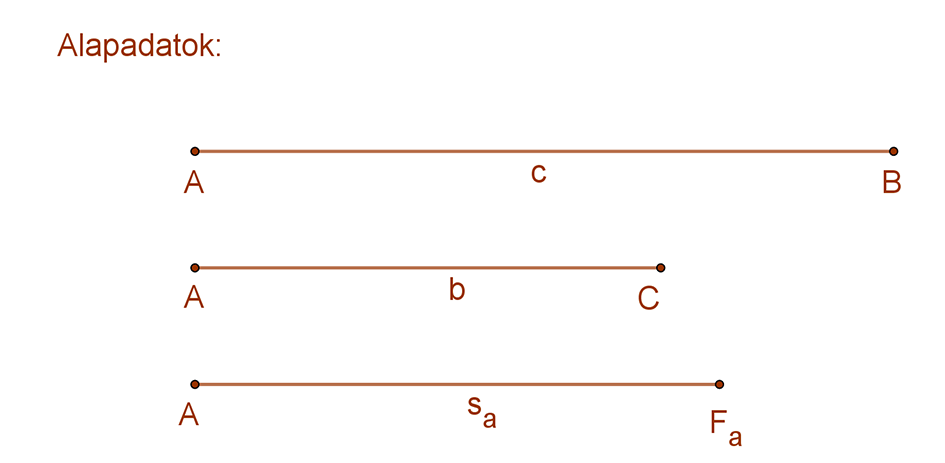

Szerkesszünk háromszöget, ha adott két oldalának és az általuk közrefogott súlyvonalnak a hossza!

Megoldás:

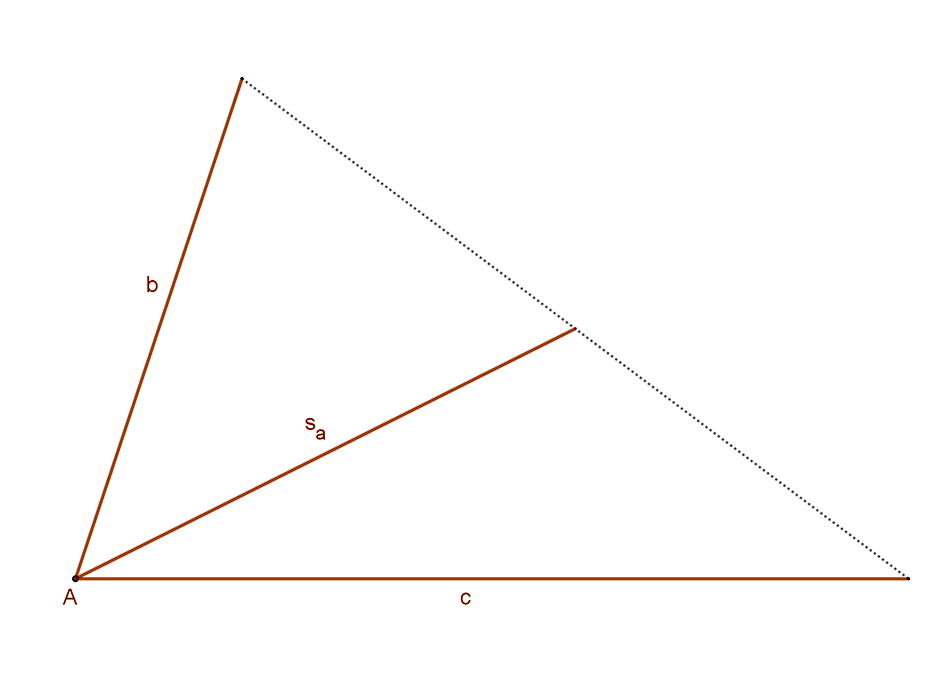
Az hamar felismerhető, hogy a háromszög „közvetlenül” nem szerkeszthető!

Ha azonban figyelembe vesszük, azt, hogy ha egy háromszöget egy oldalának felezőpontjára tükrözünk, akkor egy olyan 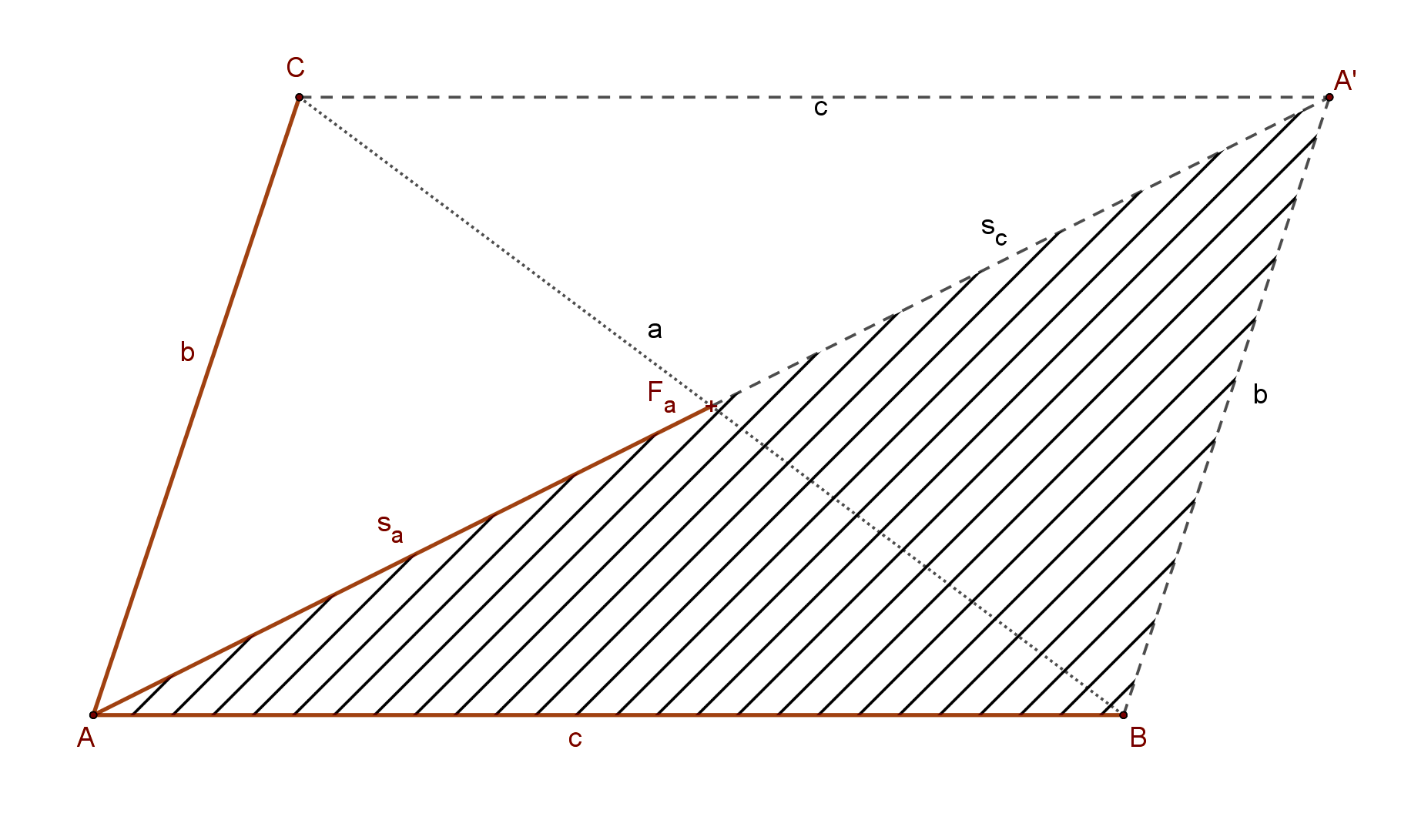paralelogrammát kapunk, amelynek két oldala a háromszög megadott két oldalával megegyezik. Továbbá az egyik átlója a háromszög a két adott oldal által közrefogott súlyvonalának a kétszerese. Ez a paralelogramma könnyen szerkeszthető, így megkapjuk a háromszöget is.

A szerkesztést az alábbi animáció szemlélteti.

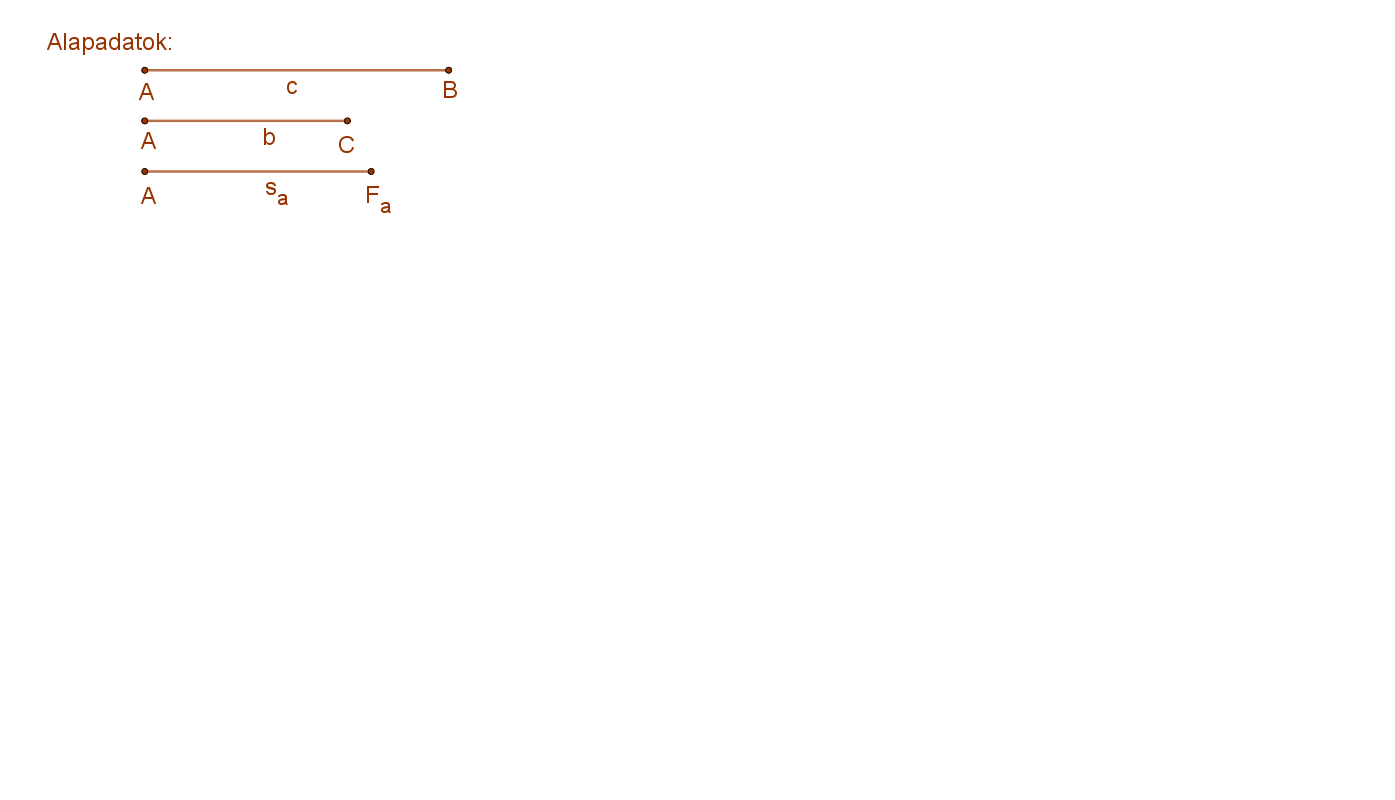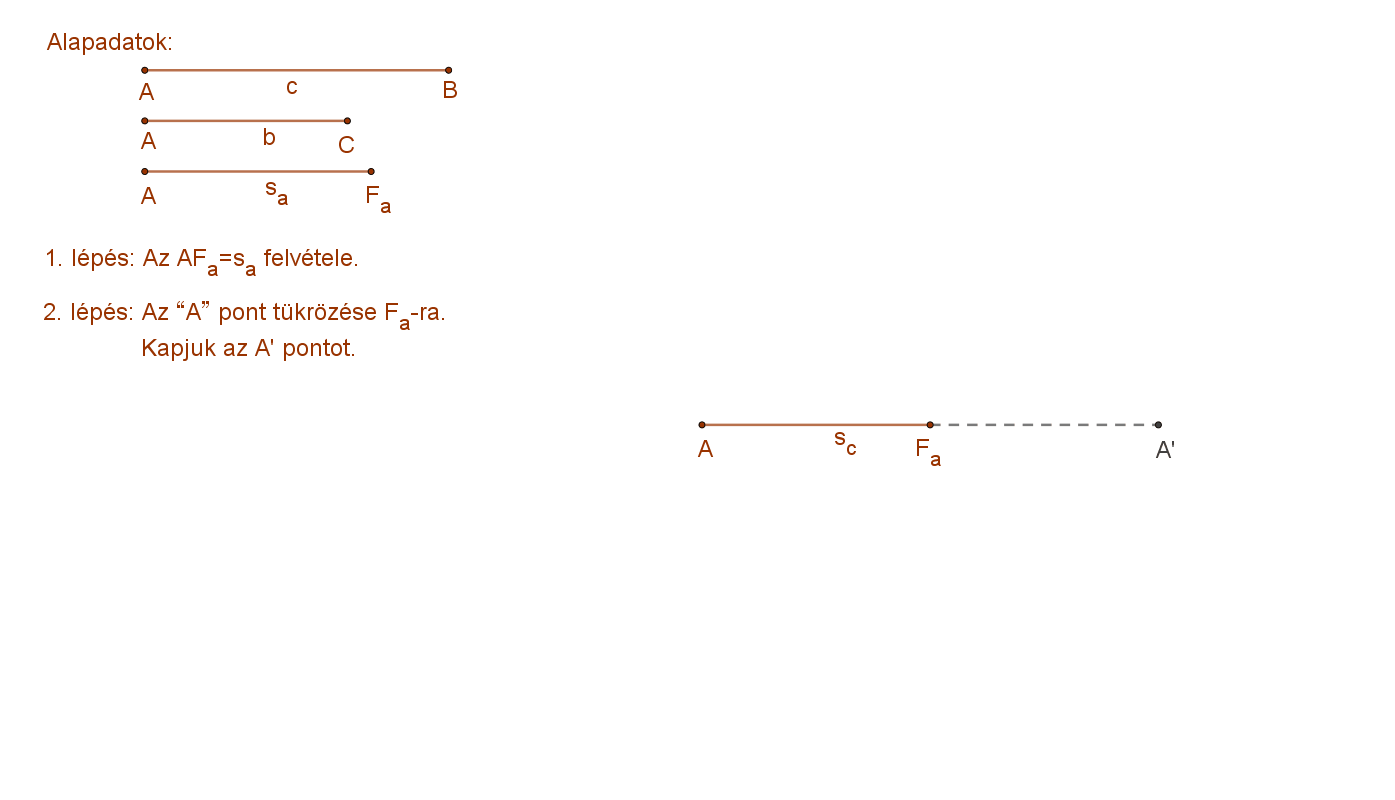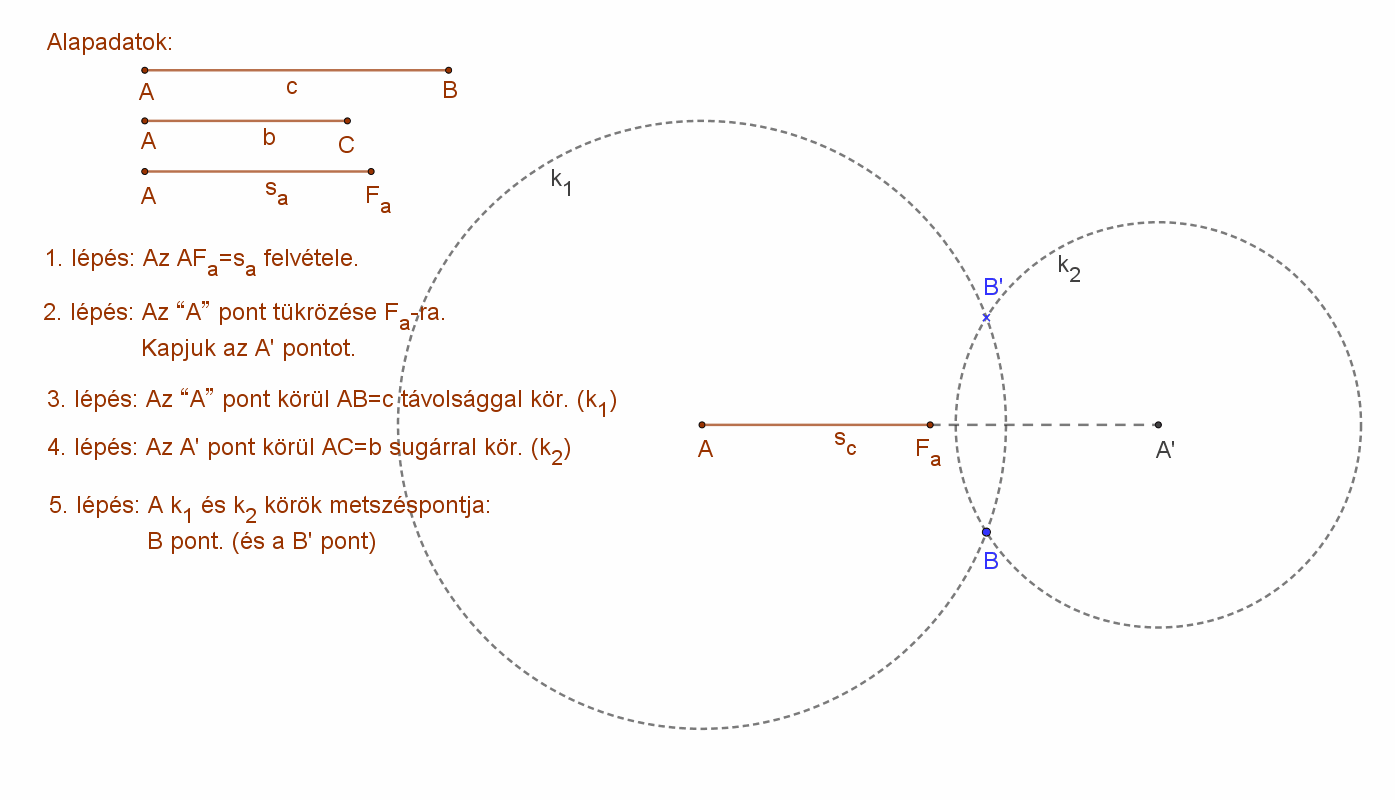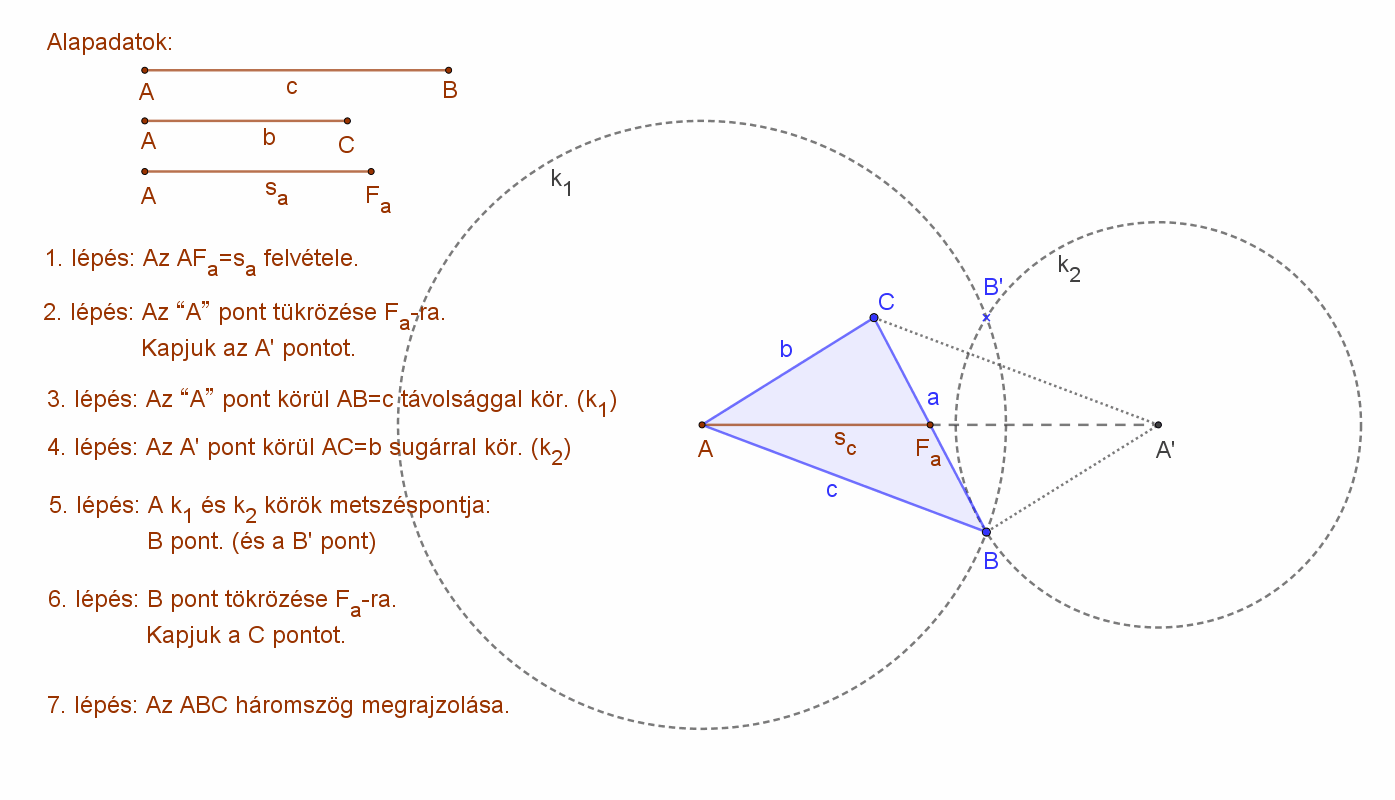
Elemzés:

Az ABC háromszög a megadott három adatból (két oldal és a köztük lévő súlyvonal) csak akkor szerkeszthető, ha a fent említett paralelogramma szerkeszthető. Itt teljesülnie kell a háromszög egyenlőtlenségnek. Azaz a háromszög súlyvonalának kétszerese kisebb kell legyen, mint a közrefogó oldalak összege.

Tétel:

Bármely háromszögben bármelyik súlyvonal hossza kisebb, mint a közrefogó oldalak számtani közepe.

Formulával: ​\( s_{a}<\frac{b+c}{2} \)​, ​\( ​ s_{b}<\frac{a+c}{2} \)​, ​\( s_{c}<\frac{a+b}{2} \)​.