Szögfelező tétel

A szögfelező tétel egy háromszögben egy adott csúcshoz tartozó szögfelezőnek az oldalakkal kapcsolatos viszonyára vonatkozik.

Ha egy egyenlőszárú háromszögben meghúzzuk a szárak által közrefogott szög felezőjét, akkor az a háromszöget két egybevágó háromszögre vágja. Ebben az esetben a szögfelező egyben szimmetriatengely is és a szemközti oldalnak felező merőlegese.

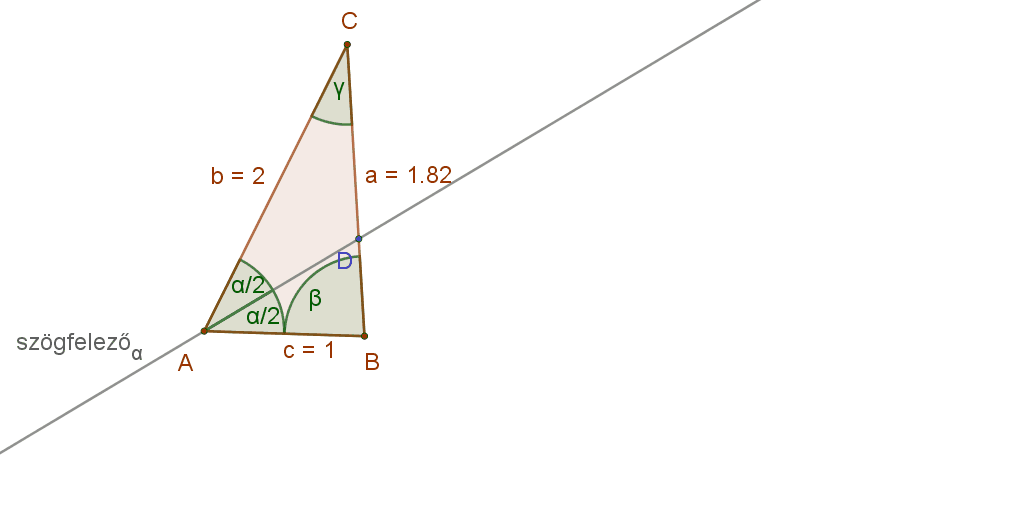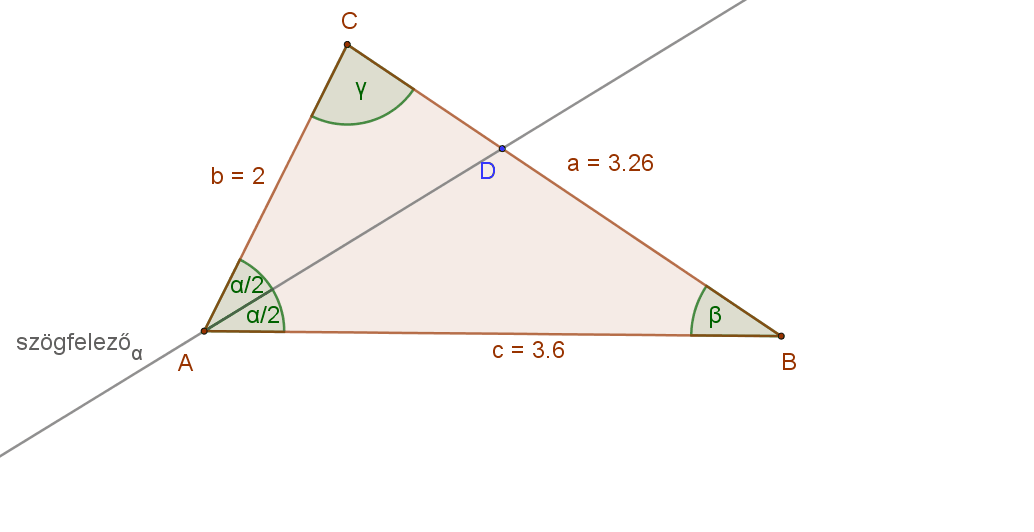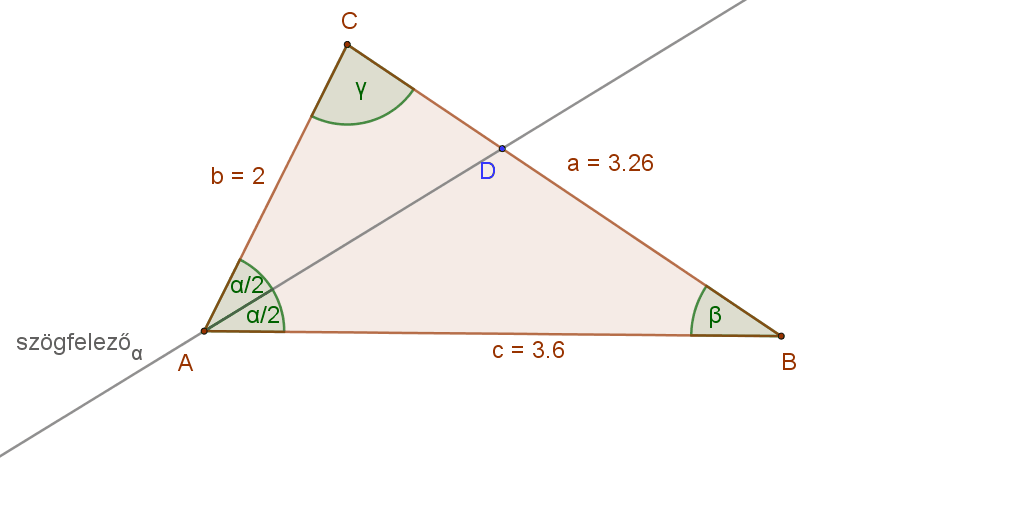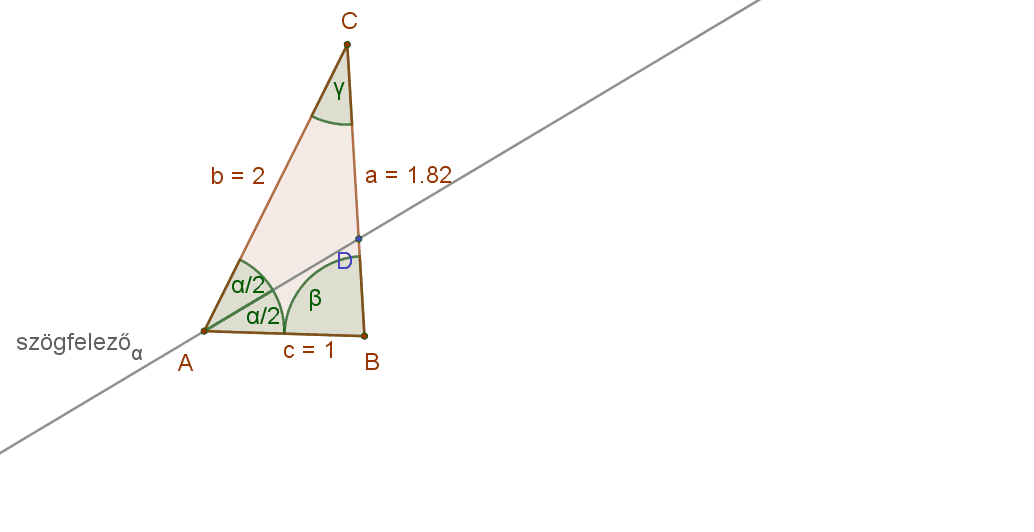
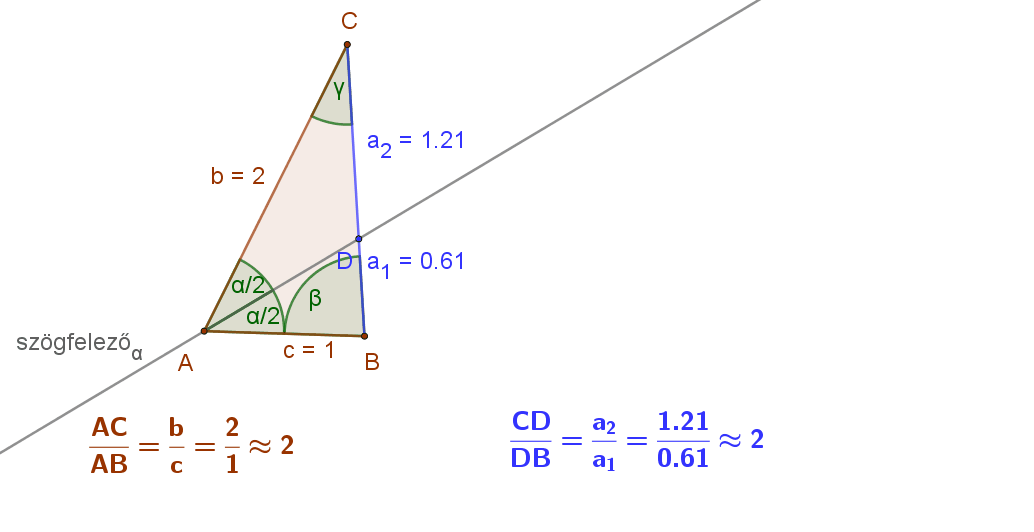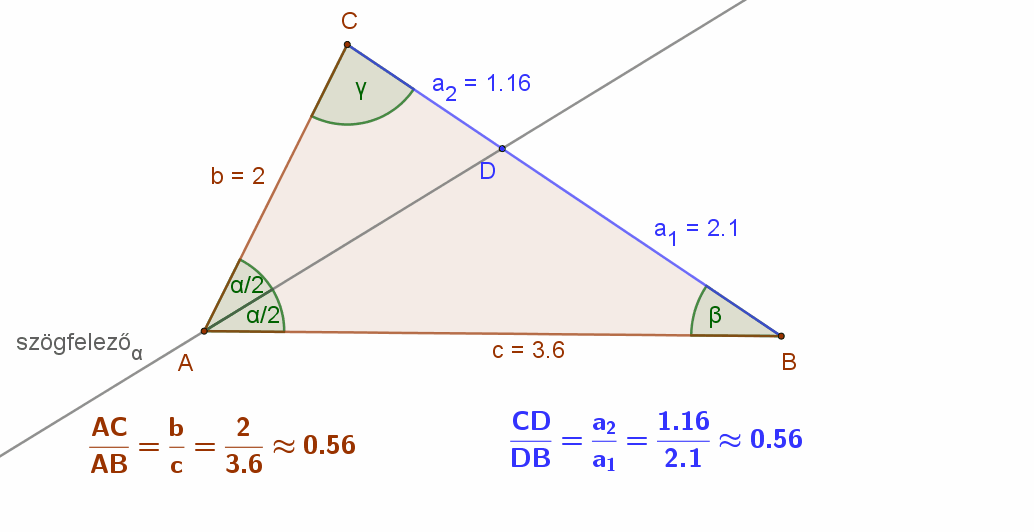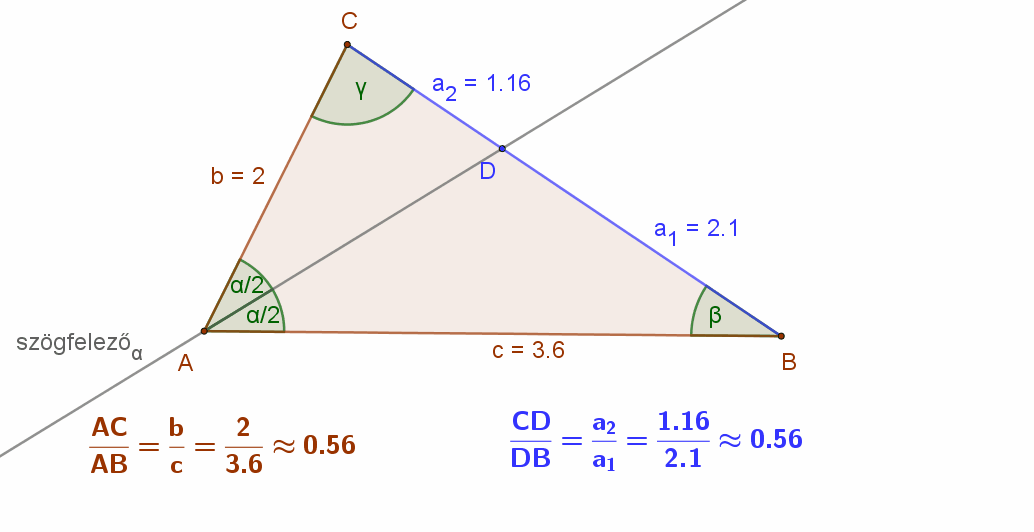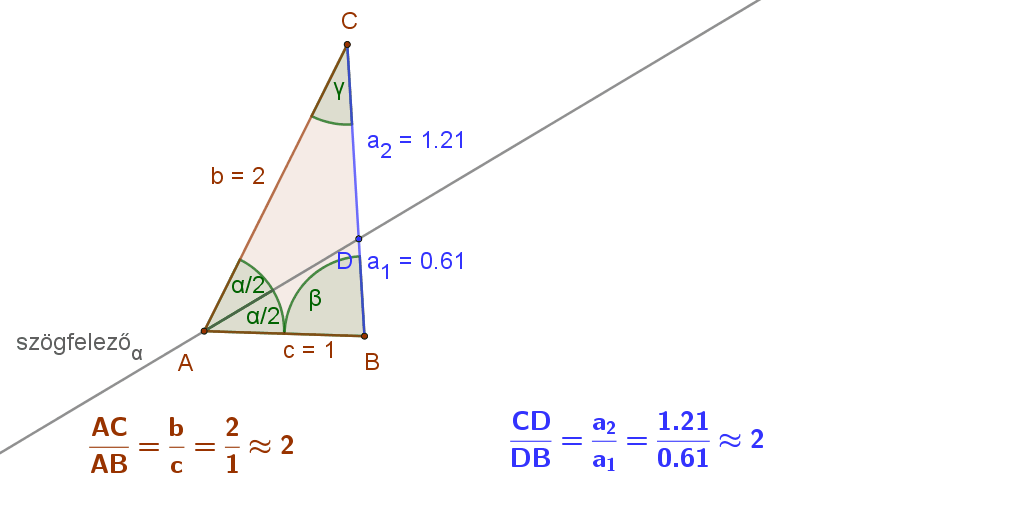
Figyeljük meg az alábbi animáción egy általános háromszögben egy adott csúcshoz tartozó szögfelező és a szemközti oldal metszéspontjának a helyzetét. Mit tapasztalunk?

Az ABC háromszög A csúcsához tartozó szögfelező D metszéspontja mindig a rövidebbik közrefogó oldal csúcsához van közelebb. Persze, ha a szögfelezőt közrefogó oldalak hossza egyenlő, akkor a D pont felezi a szemközti oldalt.

Tétel: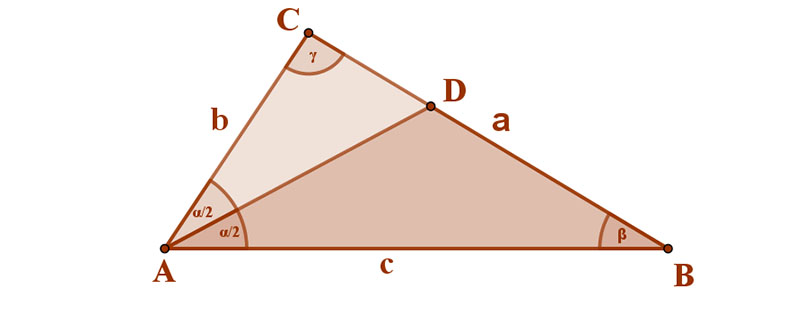

A háromszög belső szögfelezője a szemközti oldalt a szomszédos oldalak hosszának arányában osztja két részre.

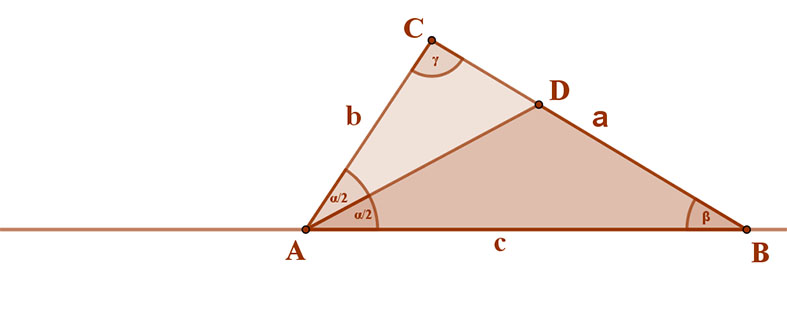
A mellékelt ABC háromszögben az A csúcsnál lévő α szög felezője a szemközti oldalt a D csúcsban metszi.  A bizonyítandó állítás: CD:DB=AC:AB

Bizonyítás:

Hosszabbítsuk meg az AB=c oldal egyenesét A csúcson túl.

 

 

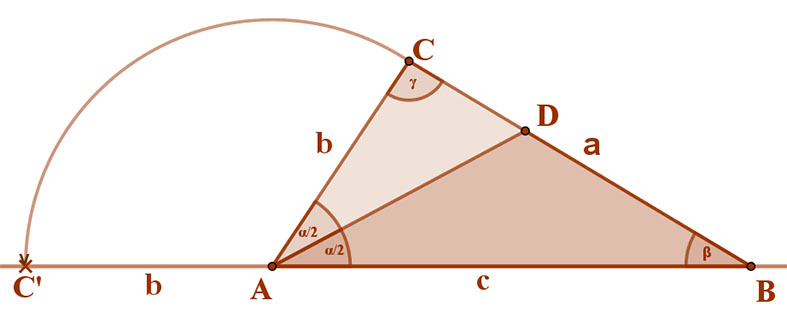
Forgassuk le erre az AC=b oldalt az A pont körül. Így kapjuk a C’ pontot.

 

 

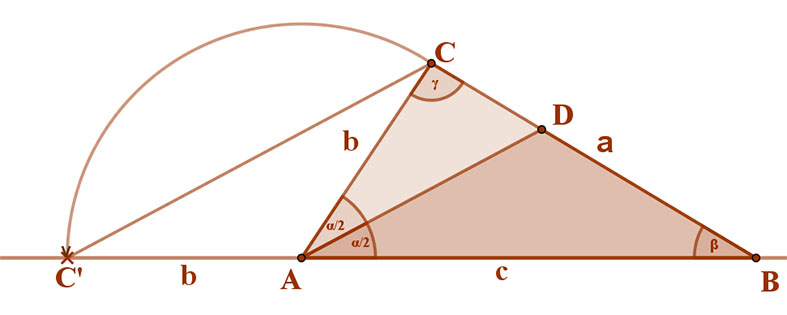
Kössük össze a kapott C’ pontot a háromszög C csúcsával. Vizsgáljuk meg az AC’C háromszöget.

Az AC’C háromszög egyenlőszárú, hiszen AC’=AC, Ezért AC’C∠ =C’CA∠ . Mivel BAC∠ külső szöge az AC’C háromszögnek, ezért AC’C∠ =C’CA∠ =α/2.
Emiatt AC’C∠ =BAD∠ =α/2.

Mivel ez a két szög egyenlő és C’A és AB egy egyenesbe esik, ezért a két szög egyállású. Tehát AD párhuzamos C’C-vel.

A párhuzamos szelők tétele szerint CD:DB=C’A:AB.

Mivel C’A=AC, így az arány: CD:DB=AC:AB.

Ezt kellett bizonyítani.

Felmerülhet ezek után az a kérdés, hogy vajon két belső szögfelező milyen arányban osztja egymást?

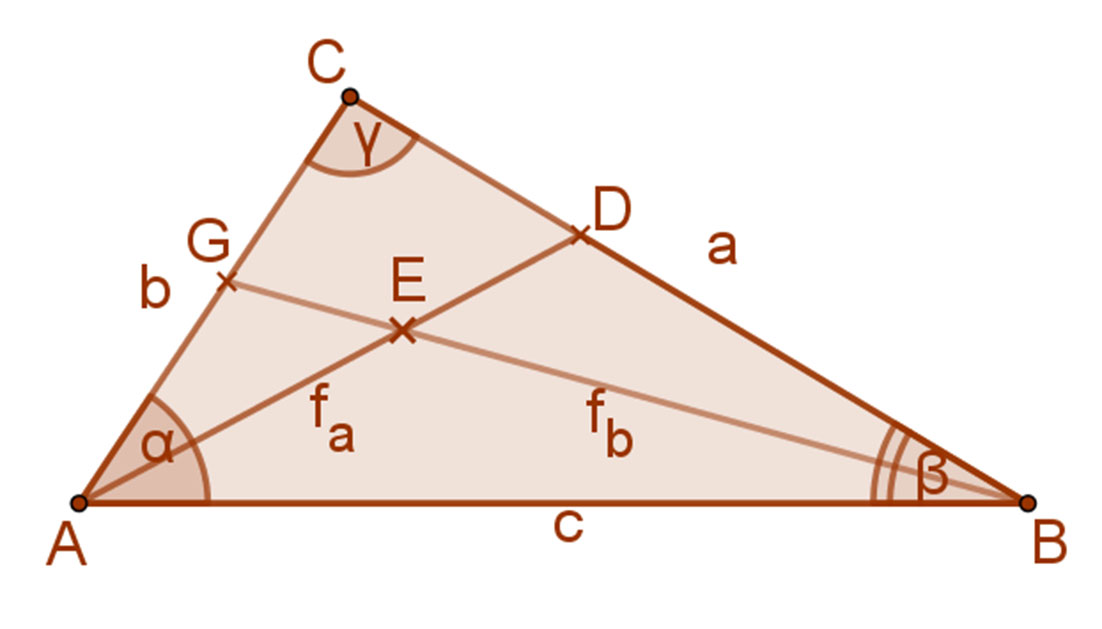Tekintsük a mellékelt ábrán az ABC háromszöget. Ebben a háromszögben az A csúcsból induló  f_a  szögfelező a CB=a oldalt a D pontban metszi.
A fenti szögfelező tétel szerint a D pont a CB-t a közrefogó oldalak arányában osztja.

Az arányos osztás elve szerint a CB=a oldalt fel kell osztani c+b részre, és ezt c-vel szorozva, kapjuk a DB szakaszt. Tehát: DB=a⋅c/(b+c)
Ha a szögfelező tételt ezek után az ABD háromszögre alkalmazzuk, a B csúcsból induló f_b szögfelező a szemközti AD oldalt E pontban metszi. Így AE:ED=AB:DB. AB=c és DB=a⋅c/(b+c) helyettesítéssel: AE:ED=c:(a⋅c/(b+c)). Ezt rendezve: AE:ED=(b+c)/a. Tehát a következő tételhez jutottunk:

Tétel:

Egy háromszögben egy szögfelezőt bármelyik másik a közrefogó oldalak összegének és a vele szemben levő oldal arányában osztja.
Formulával: AE:ED=(b+c)/a

Feladat:

Igazolja, hogy ha egy derékszögű háromszögből az egyik hegyesszög szögfelezője egyenlőszárú háromszöget metsz le, akkor azon szögfelező a szemközti oldalt 1:2 arányban osztja!

(Összefoglaló feladatgyűjtemény 1720. feladat.)

Megoldás:

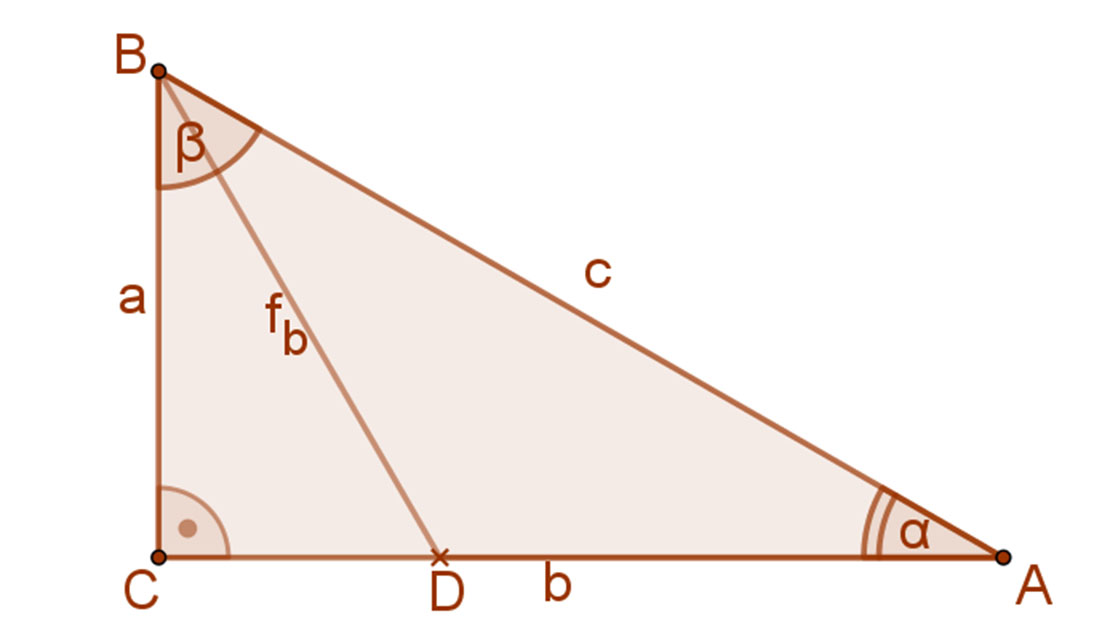Csakis az ABC derékszögű háromszög nagyobbik hegyesszögének szögfelezőjéről lehet szó. Hiszen a feltétel szerint egyenlőszárú háromszögnek kell keletkeznie, azaz a másik hegyesszög meg kell egyezzen a megfelezett szög felével. A mellékelt rajzon DAB∠=DBA∠, mivel a BDA háromszög egyenlő szárú, ezért DA=DB.

Másrészt BD szögfelező, ezért CBD∠=DBA∠=DAB∠. CBD∠+DBA∠+DAB∠=90°, azaz mindegyik szög = 30° . Mivel a BCD derékszögű háromszögben CBD∠=30° , ezért a BD átfogó =2⋅CD, vagyis CD:BD=1:2 A feltétel szerint BD=DA, ezért CD:DA=1:2.

Ezt kellett igazolni.