Elemi függvények csoportosítása

Függvények egy lehetséges csoportosítása

1. Algebrai függvények

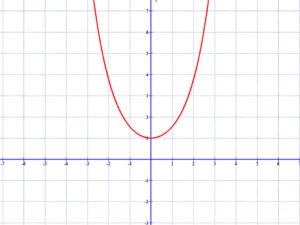
1.1 Racionális egész függvények
(például hatvány függvények)

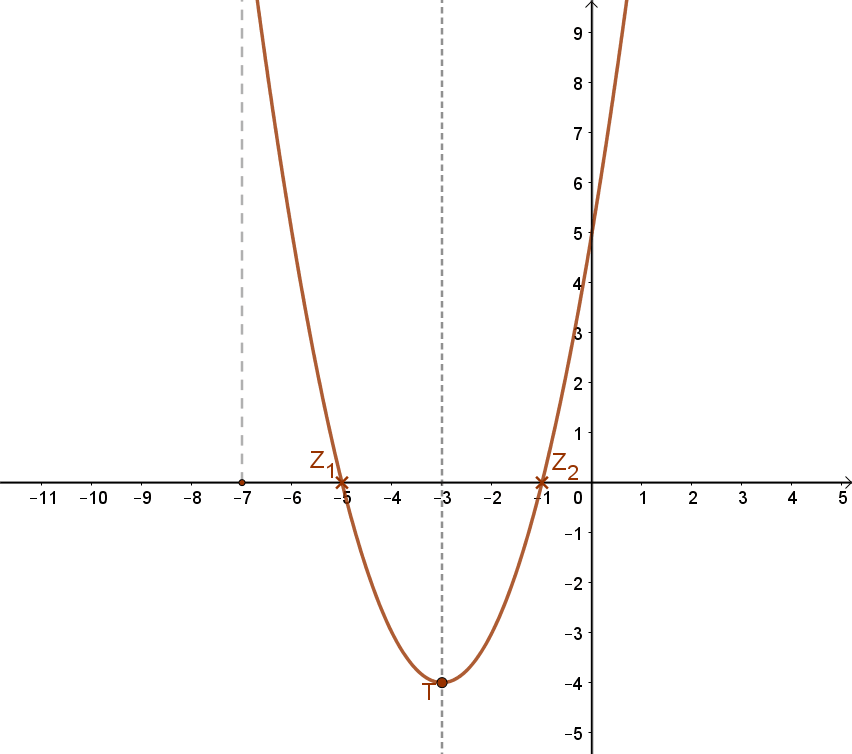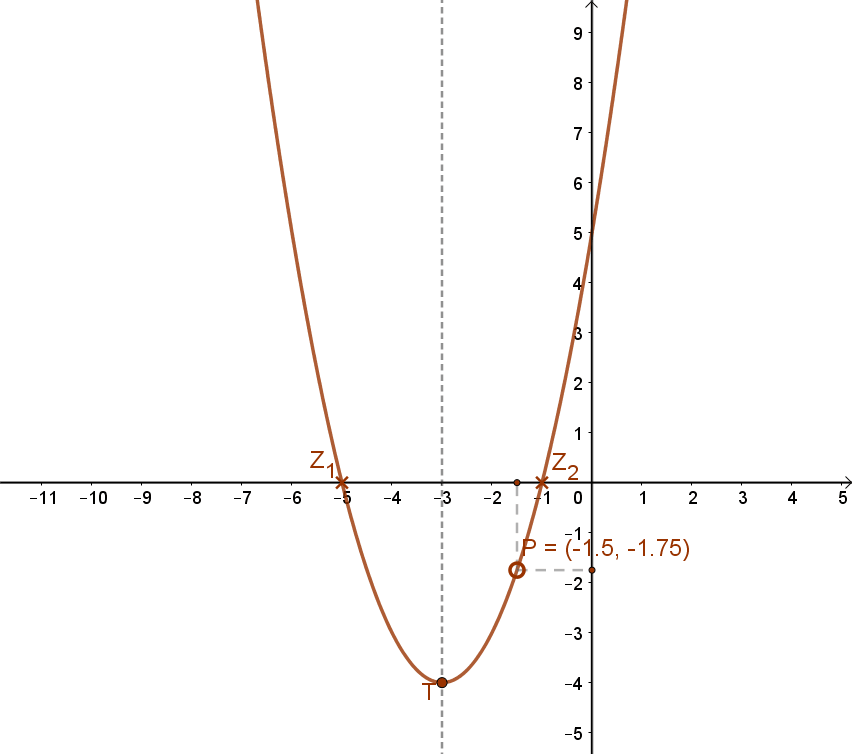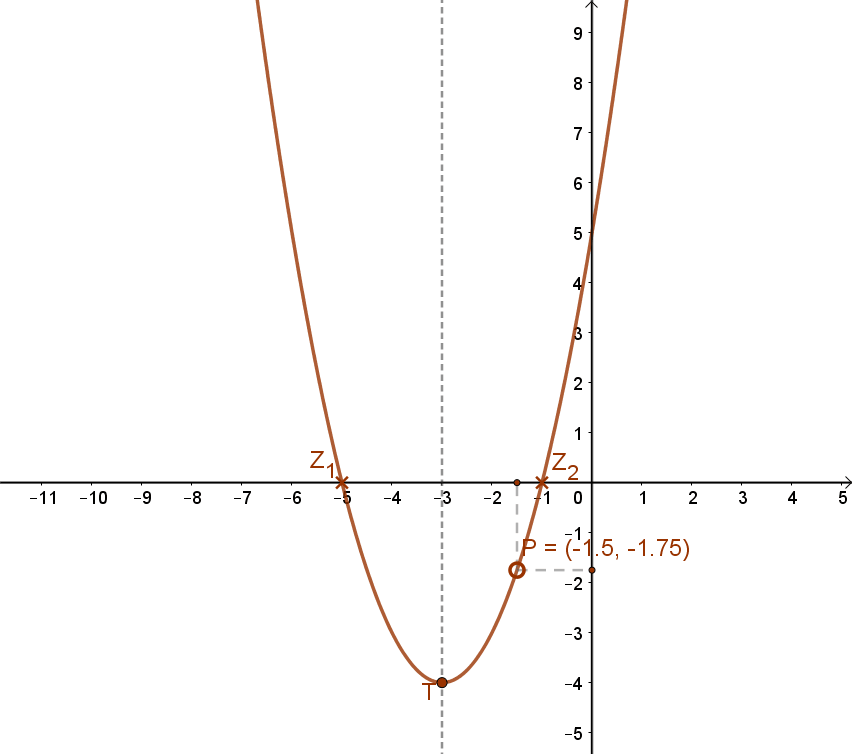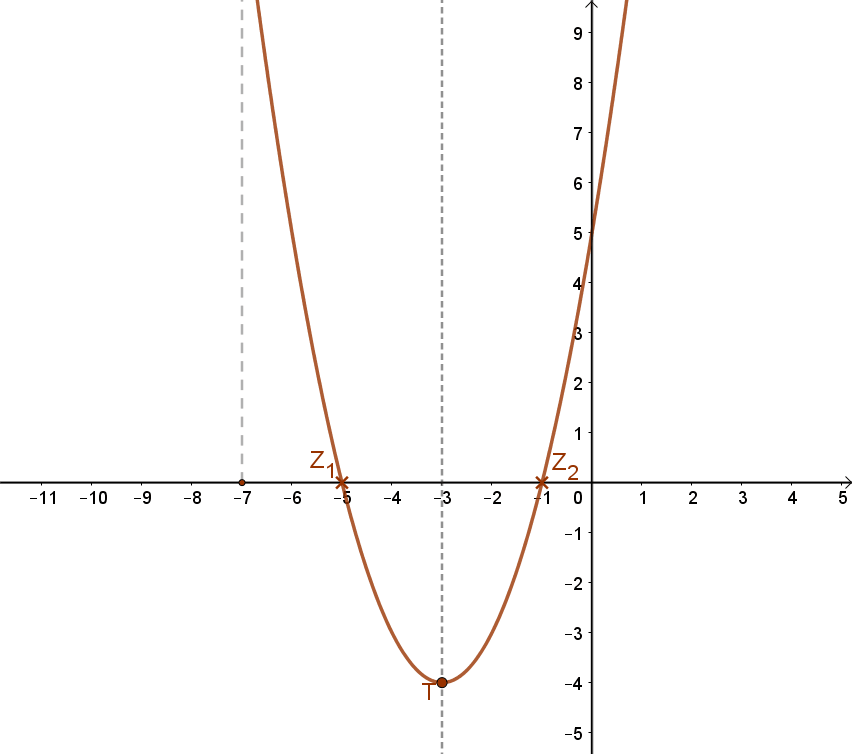m(x)=(x+3)²-4=x²+6x+5

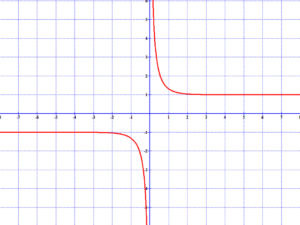
1.2 Racionális törtfüggvények
(például a reciprok függvény)

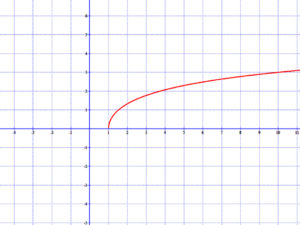
1.3 Irracionális függvények

(Például a gyökfüggvények)

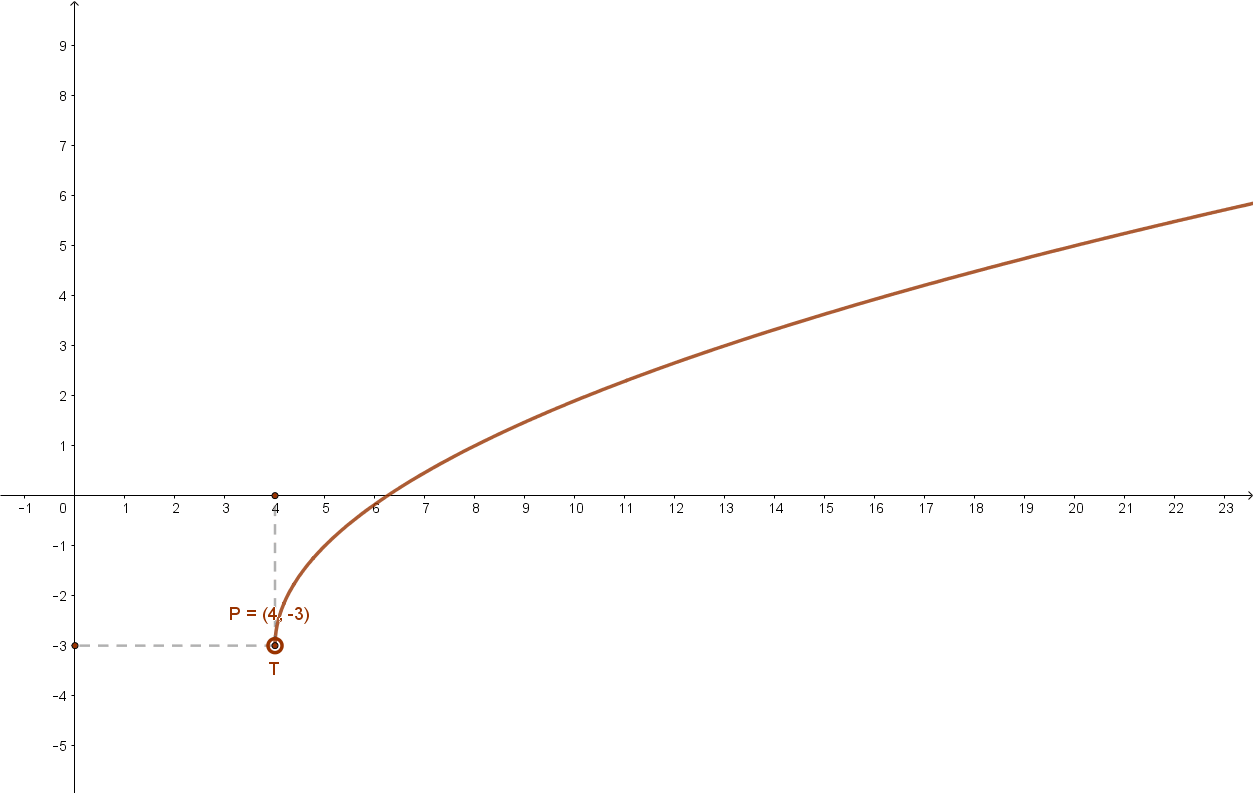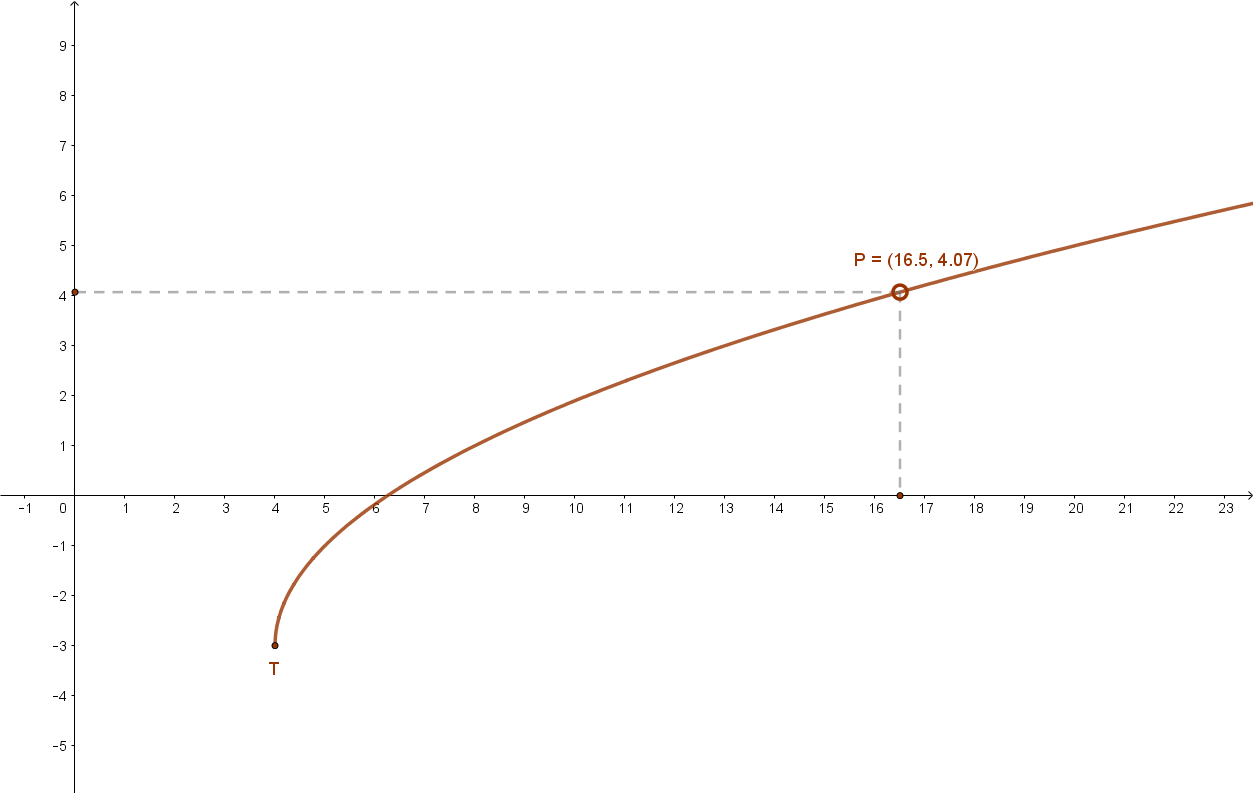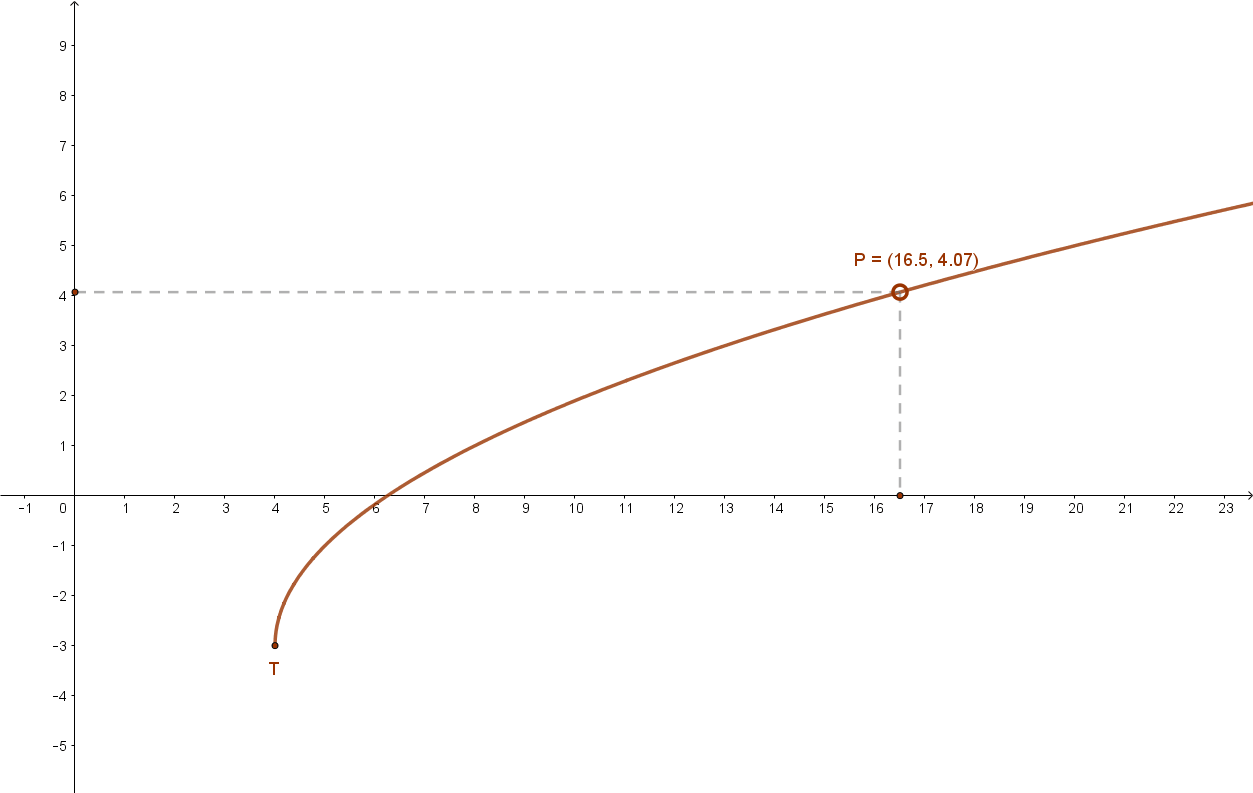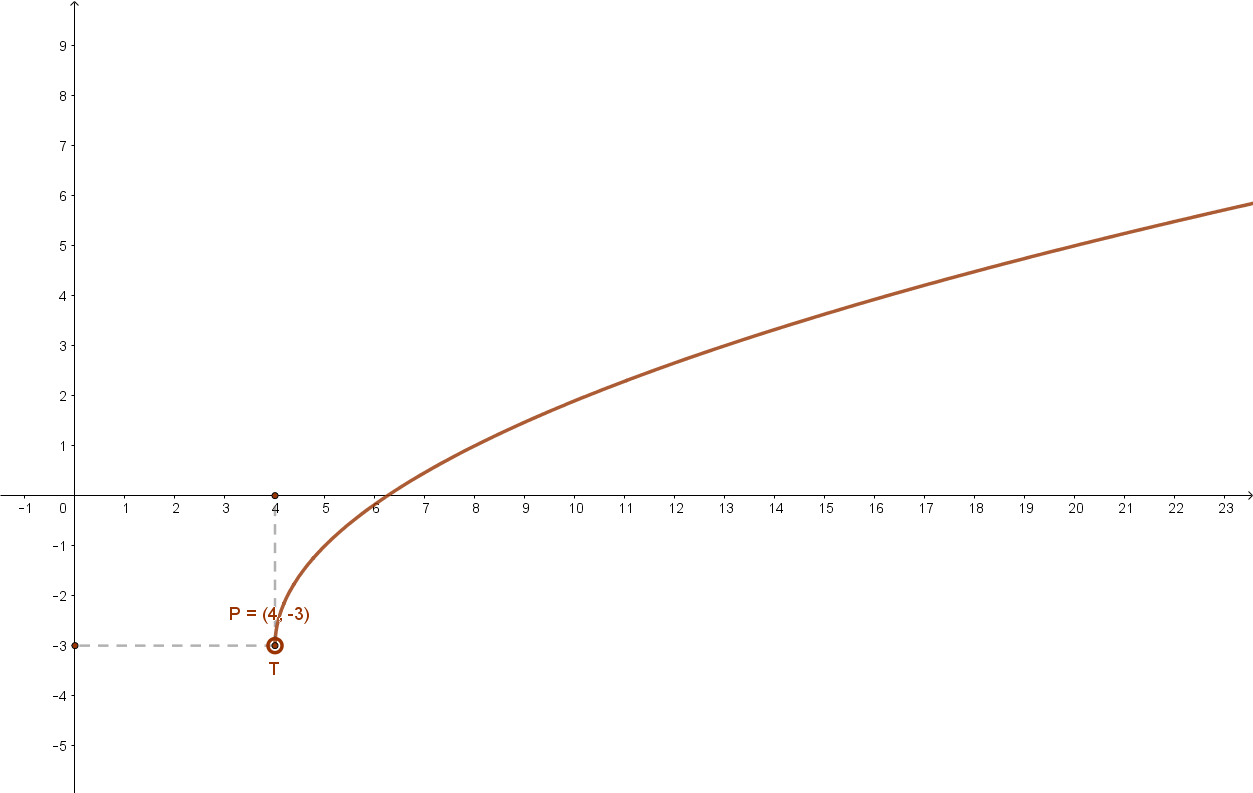
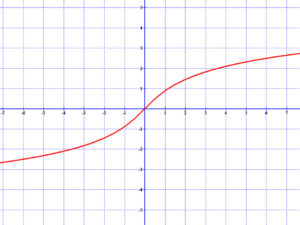
2. Transzcendens függvények

2.1 Exponenciális függvények

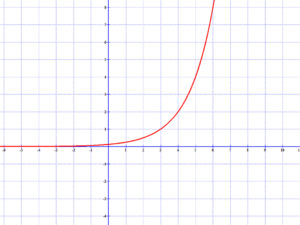​\( e(x)=0,5·2^{x-2} \)​

2.2 Logaritmus függvények

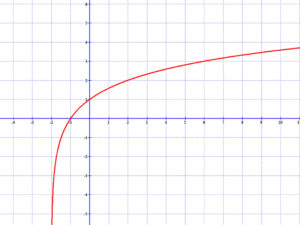
3.   Trigonometrikus függvények

3.1 Szinusz függvény

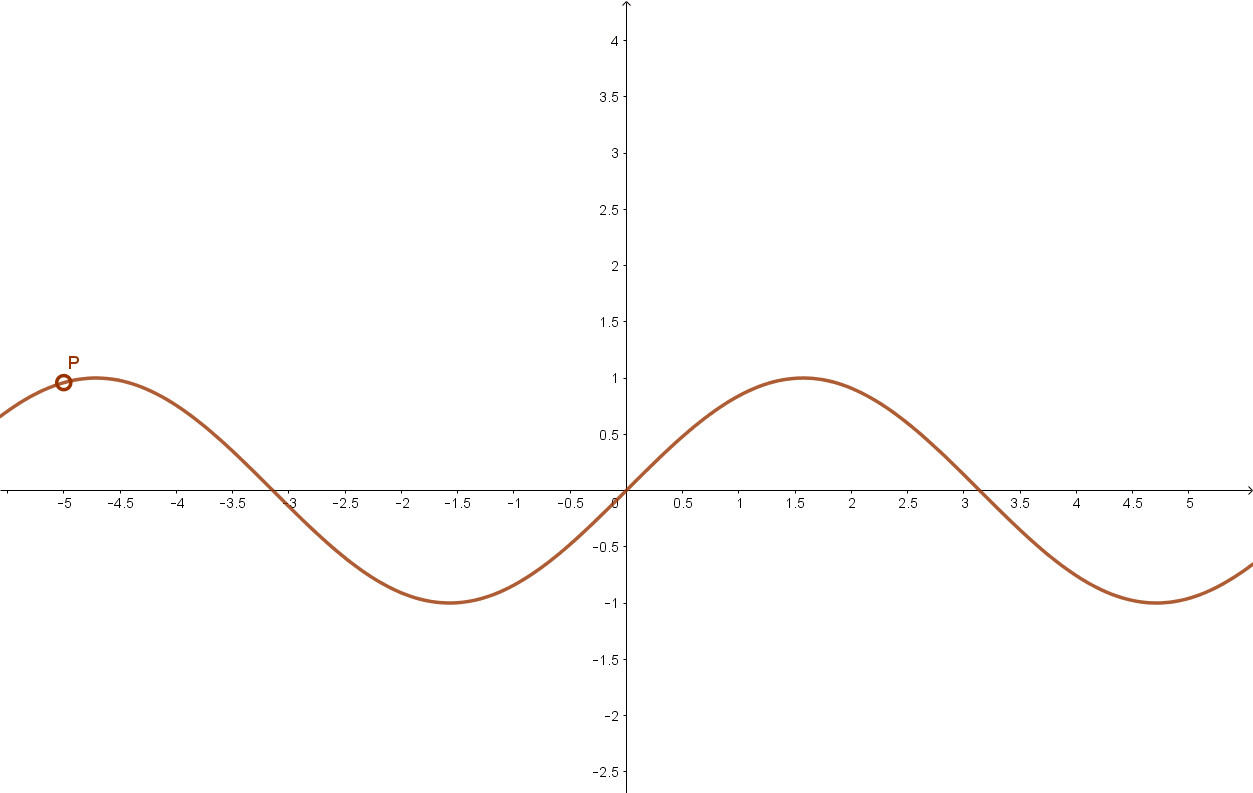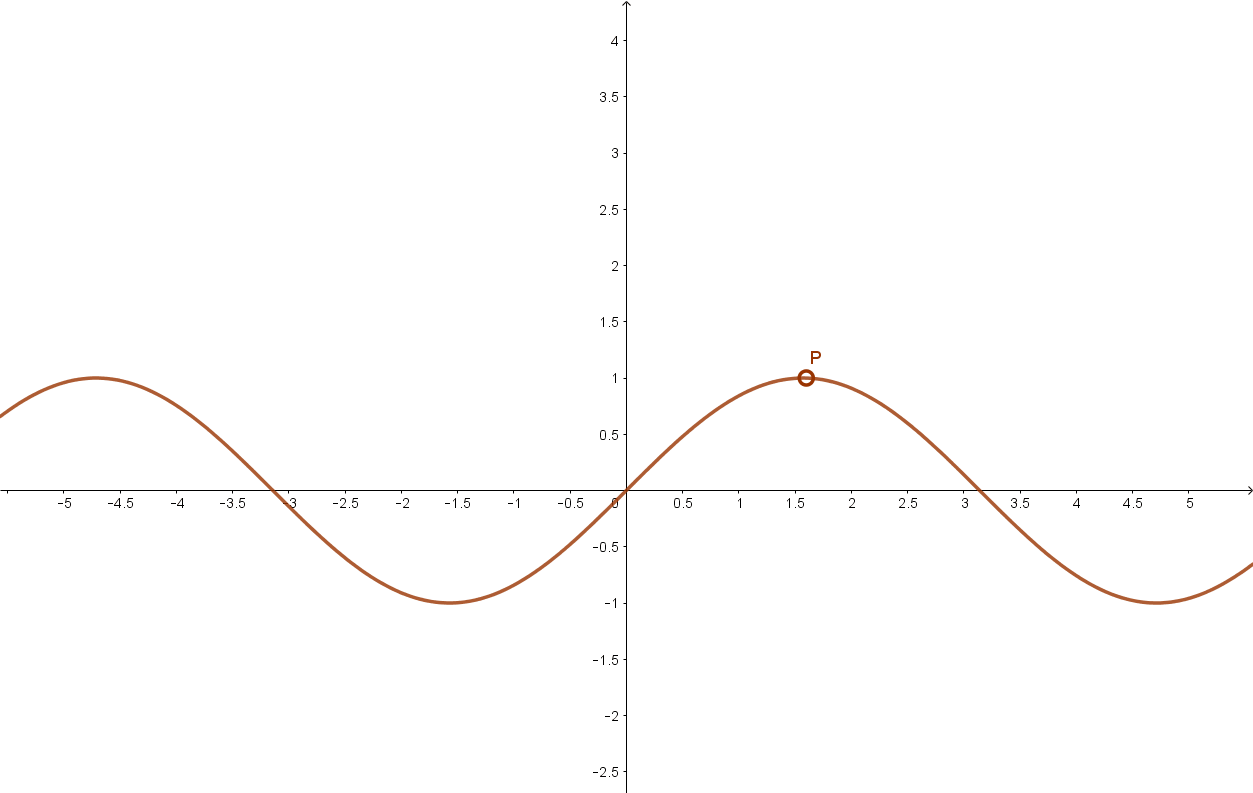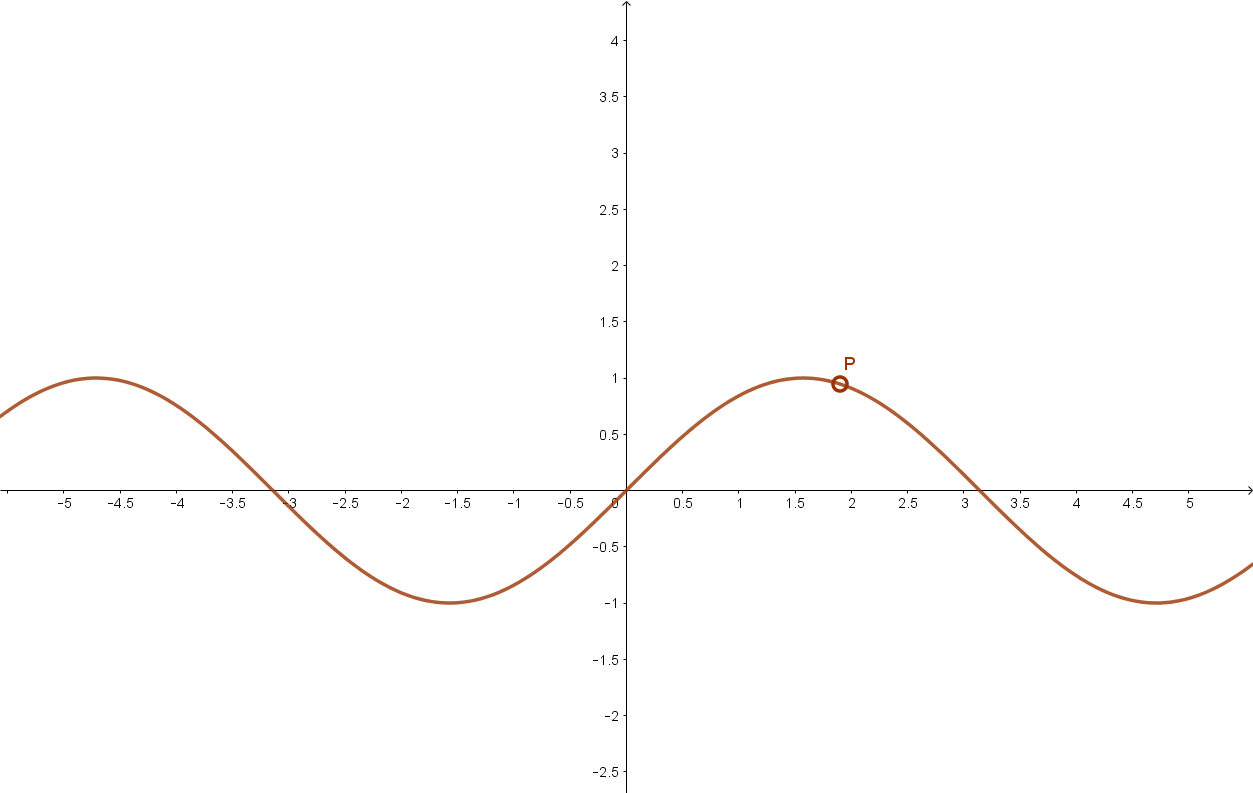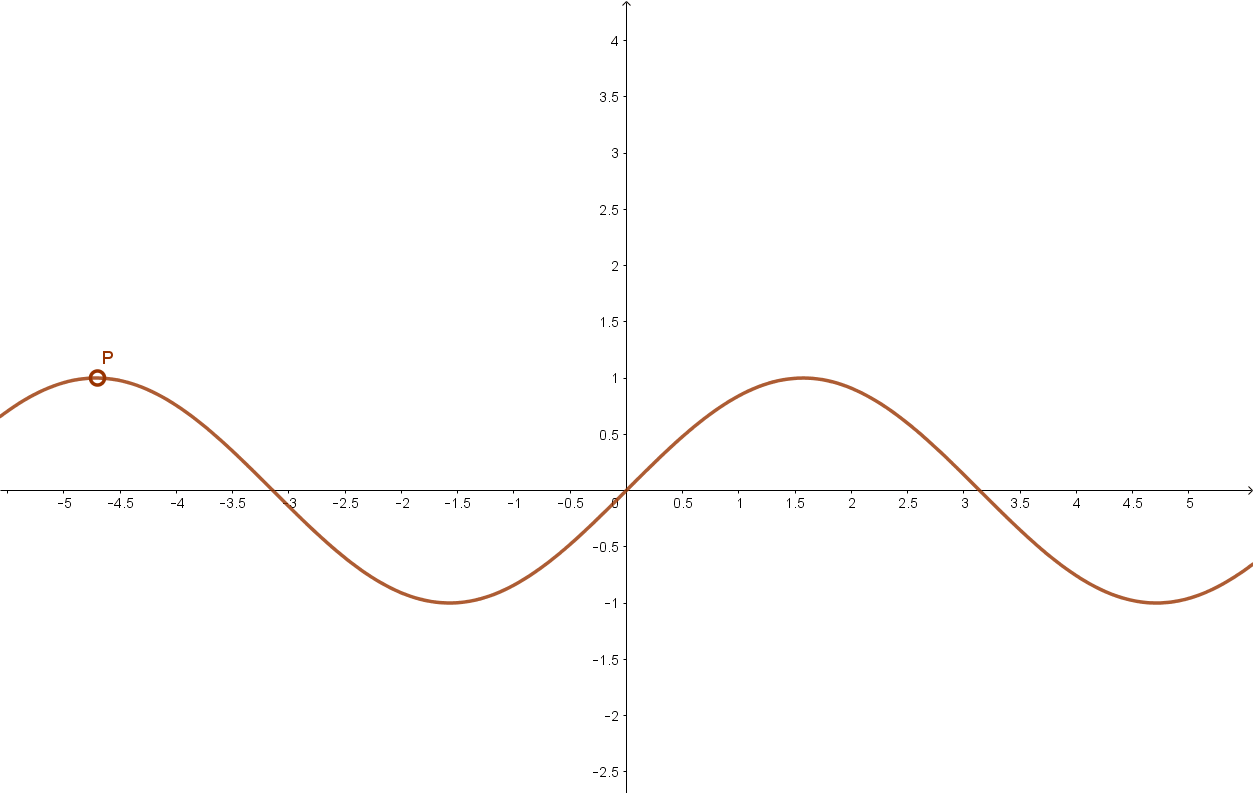
3.2 Koszinusz függvény

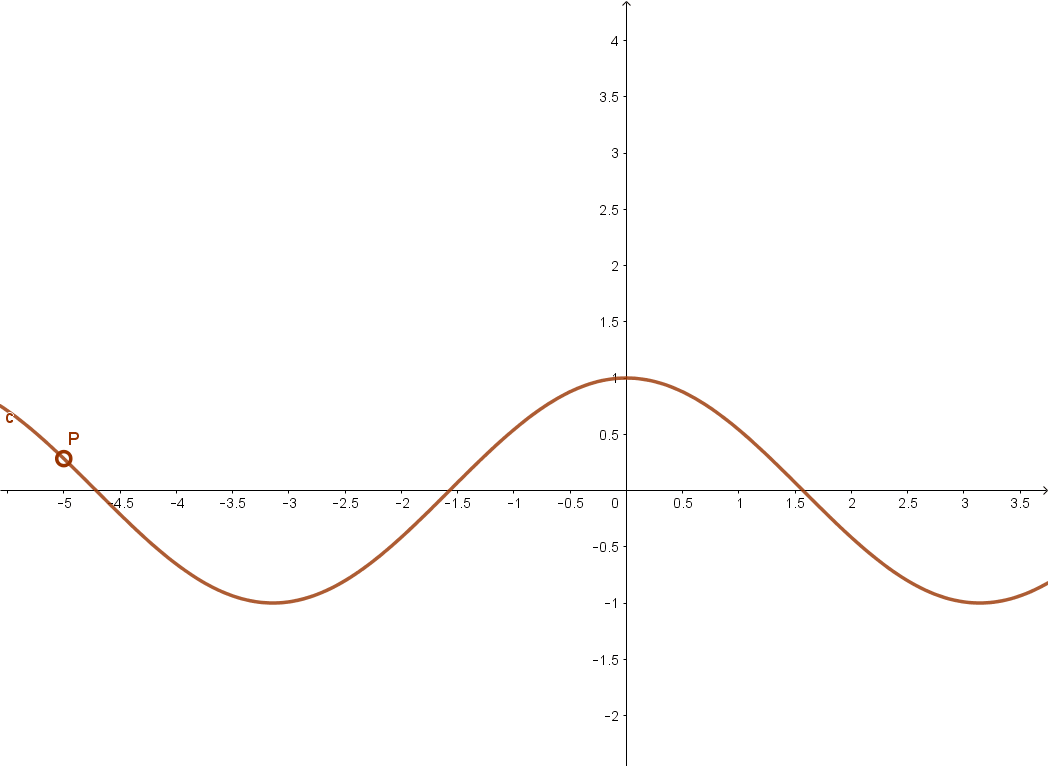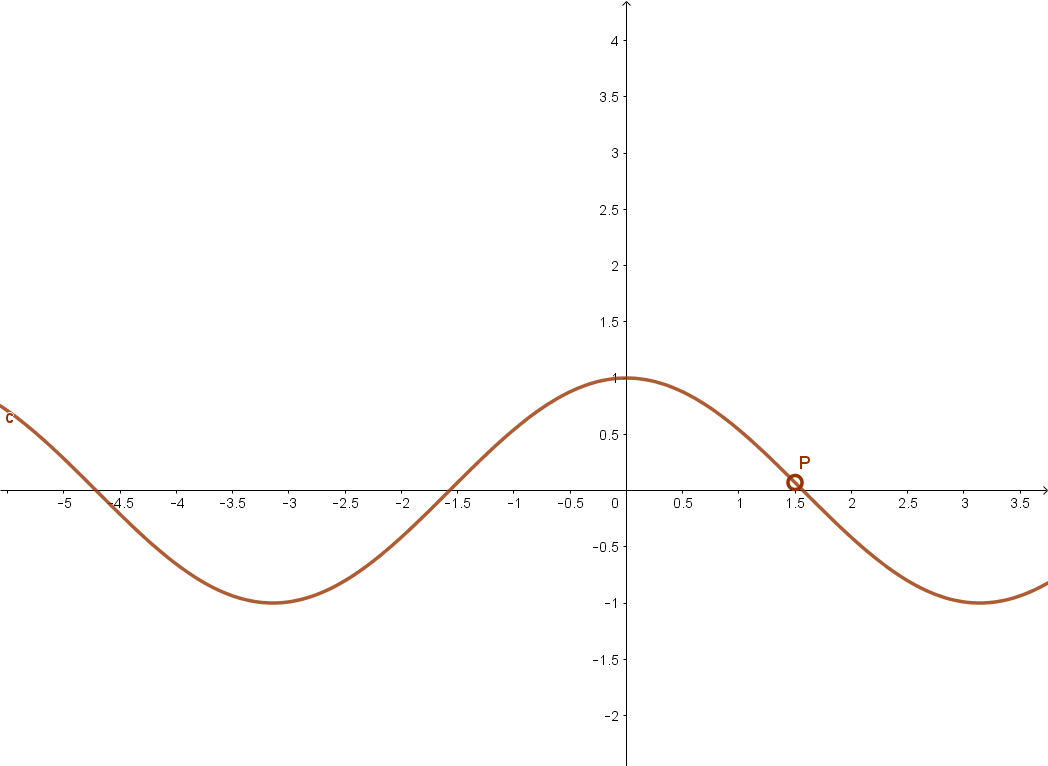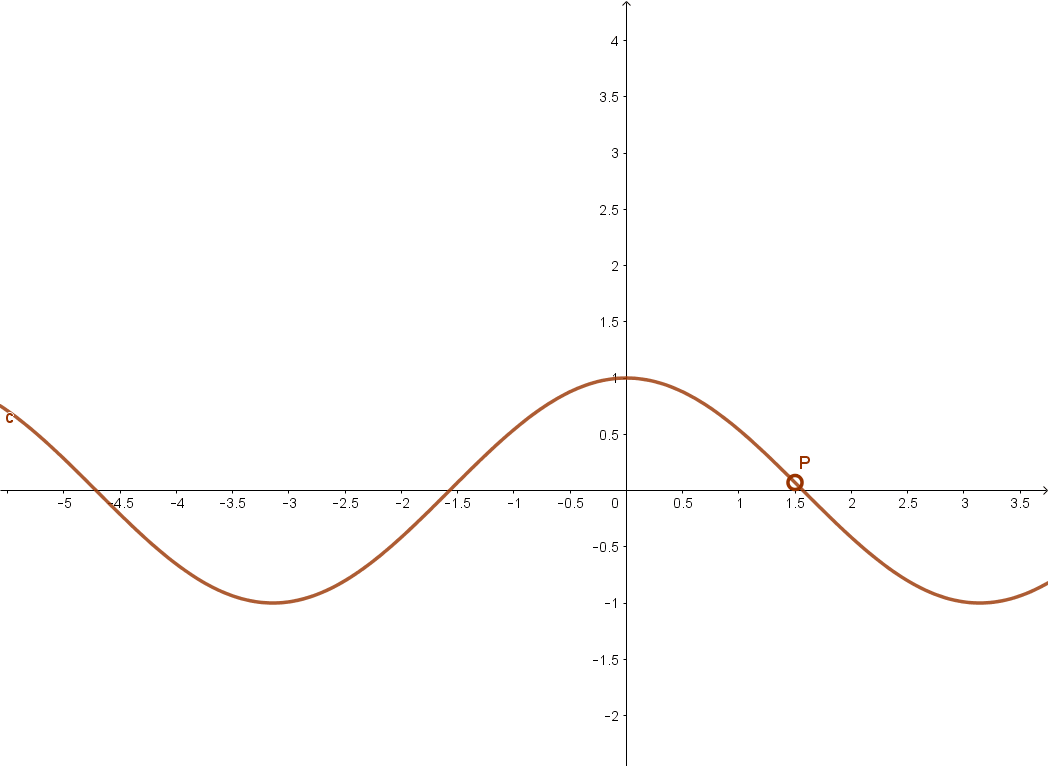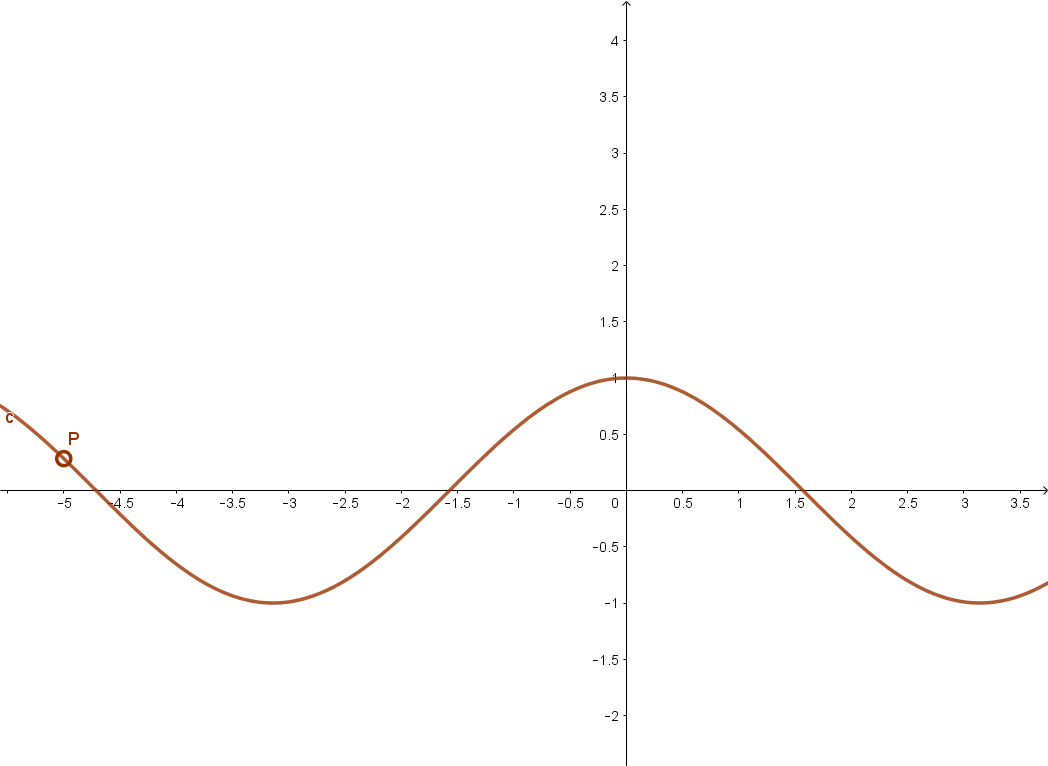
3.3 Tangens függvény

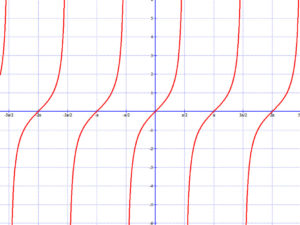
3.4 Kotangens függvény

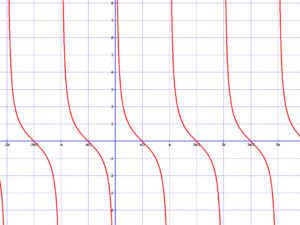
4. Trigonometrikus függvények inverzei, az arcus függvények

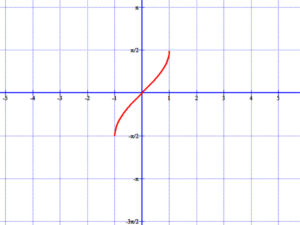
4.1 Arkusz-szinusz függvény

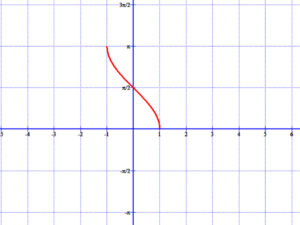
4.2 Arkusz-koszinusz  függvény

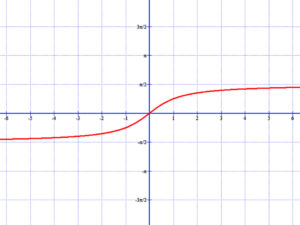
4.3 Arkusz-tangens függvény

 

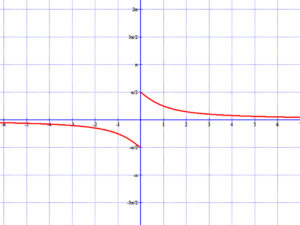
4.4 Arkusz-kotangens függvény

5. Hiperbolikus függvények

5.1 Szinusz hiperbolikus függvény

Lásd: ​\( sh(x)=\frac{e^{x}-e^{-x}}{2} \)​

5.2 Koszinusz hiperbolikus függvény

Lásd: ​\( ch(x)=\frac{e^{x}+e^{-x}}{2} \)​

5.3 Tangens hiperbolikus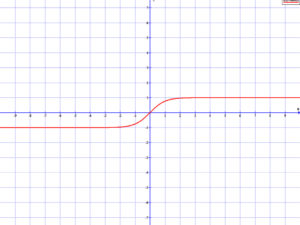

Lásd: ​\( th(x)=\frac{sh(x)}{ch(x)} \)​

5.4 Kotangens hiperbolikus

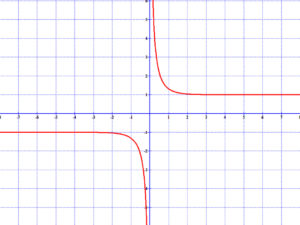Lásd: ​\( cth(x)=\frac{ch(x)}{sh(x)} \)

6. Hiperbolikus függvények inverzei, az area függvények​

6.1 Area szinusz hiperbolikus

Lásd: ​\( arsh(x)=ln\left(x+\sqrt{x^{2}+1}\right) \)​

6.2 Area koszinusz hiperbolikus

Lásd: ​\( arch(x)=ln\left(x+\sqrt{x^{2}-1}\right) \)​

6.3 Area tangens hiperbolikus

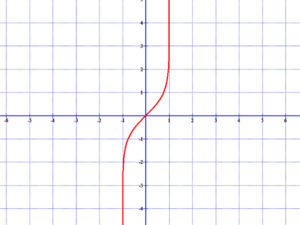
Lásd: ​\( arth(x)=\frac{1}{2}ln\left( \frac{1+x}{1-x}\right) \)​

6.4 Area kotangens hiperbolikus

 

Lásd: ​\( arcth(x)=\frac{1}{2}ln\left( \frac{x+1}{x-1}\right) \)​

7. Egyéb függvények

7.1 Abszolút érték függvény

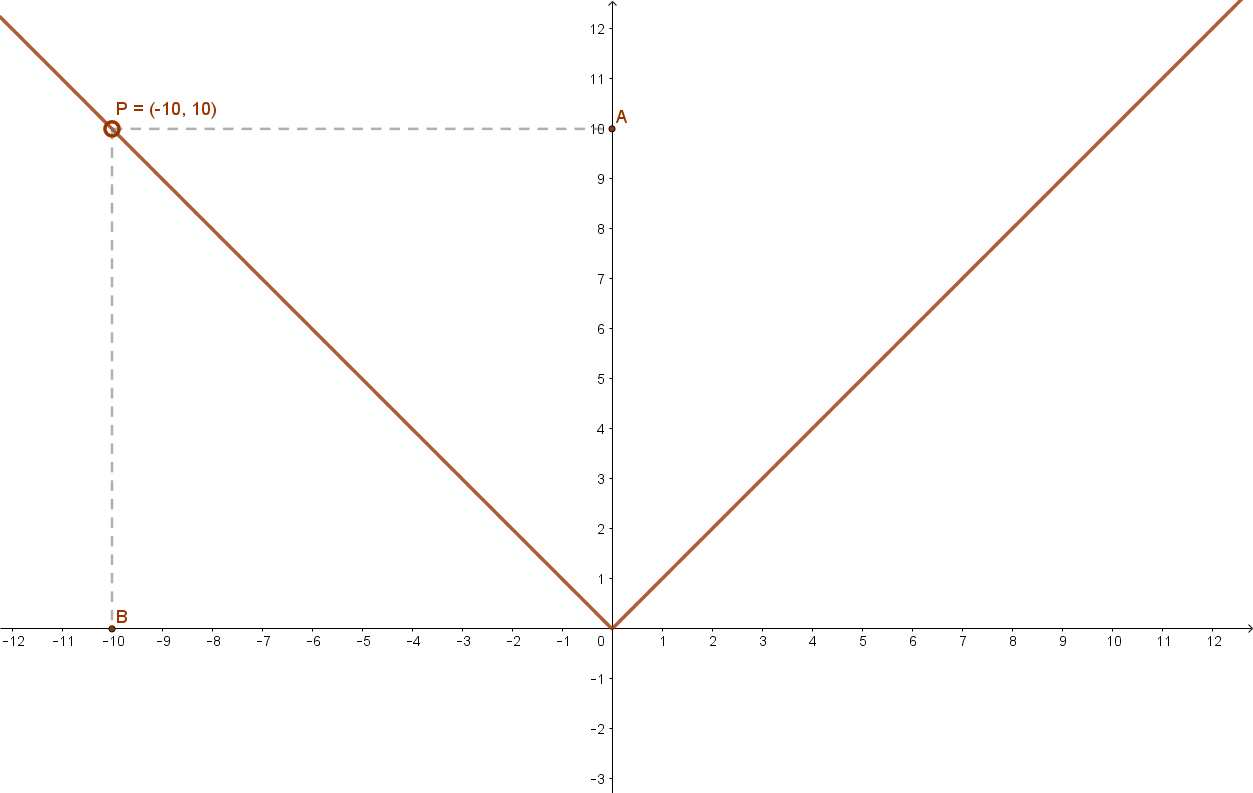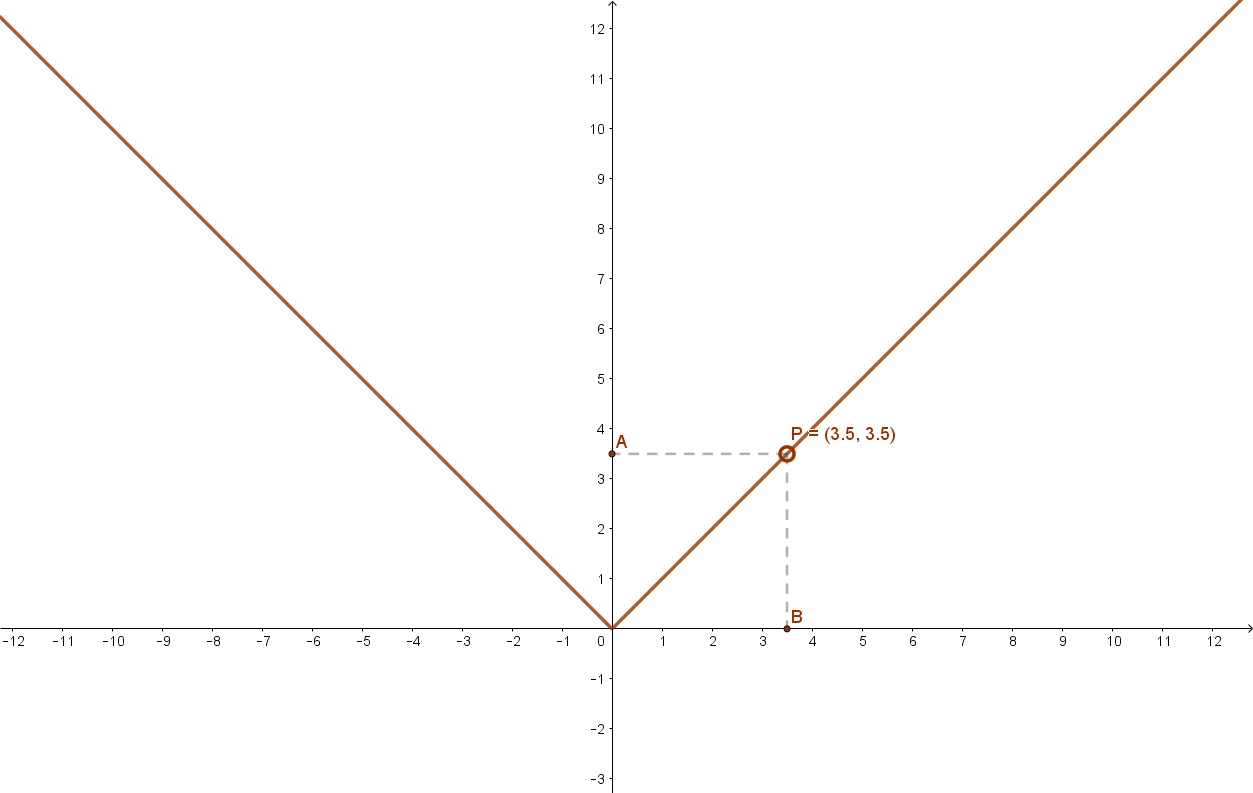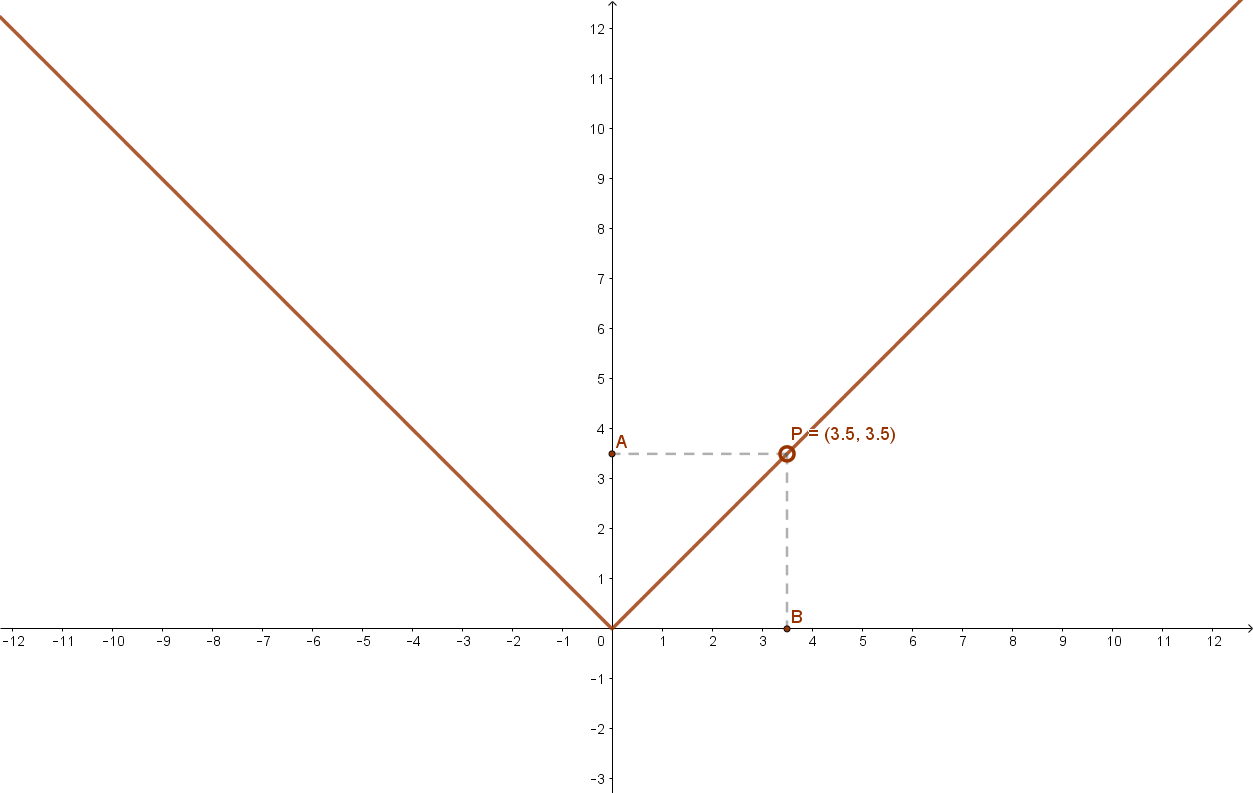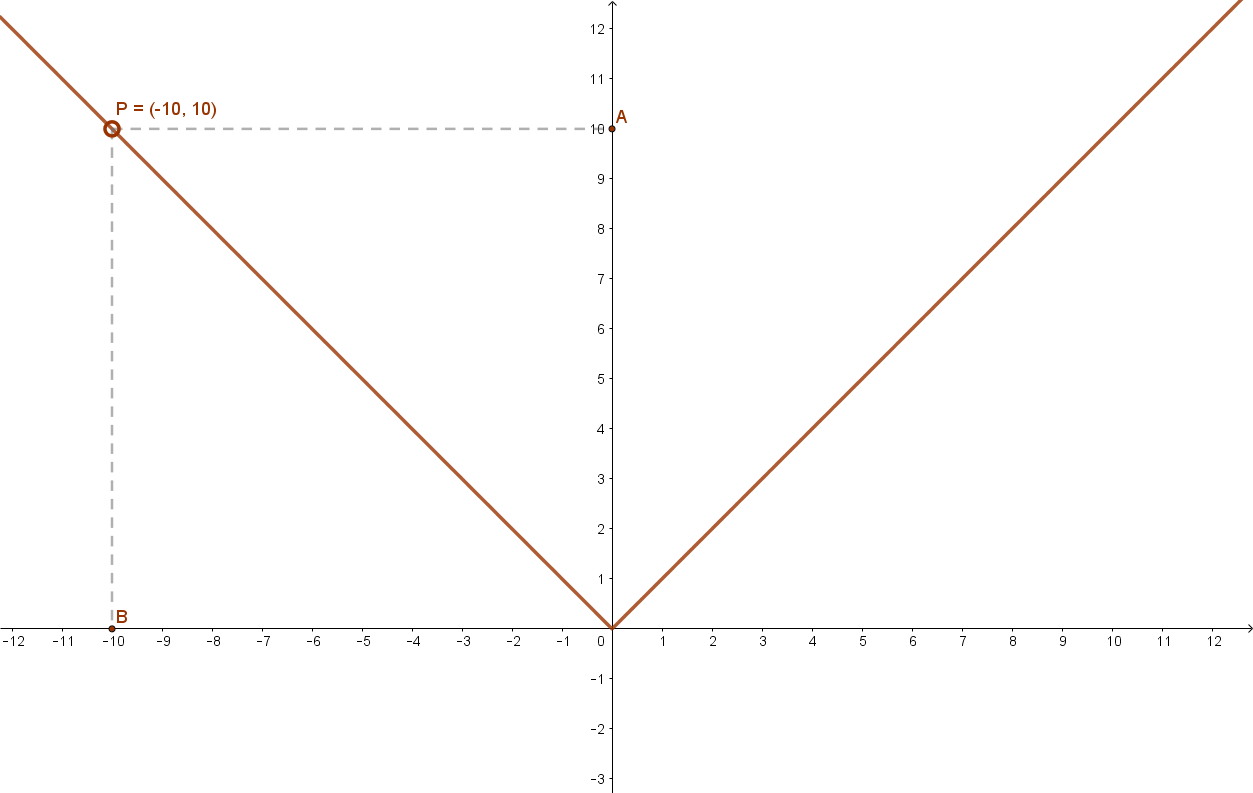
Lásd: a(x)=|x|

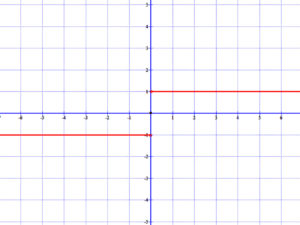
7.2 Előjel függvény

Lásd: ​​\( sgn(x)=\left\{\begin{array}{} 1, \; ha \; x>0 \\ 0, \; ha \; x=0\\ -1, \; ha \; x<0 \end{array}\right\} \)​​

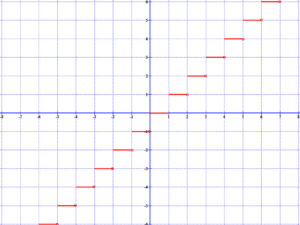
7.3 Egészrész függvény

Lásd: e(x)= [x]

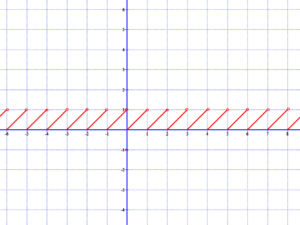
7.4 Törtrész függvény

Lásd: t(x)={x}=x-[x]

7.5 Dirichlet függvény

Nem ábrázolható!

​\( Dirichlet függvény=\left\{ \begin{array}{}1, \; ha \; x \; racionális \\\; 0, \; ha \; x \; irracionális \\ \end{array} \right\} \)​