Az x→sin(x) függvény grafikonja:
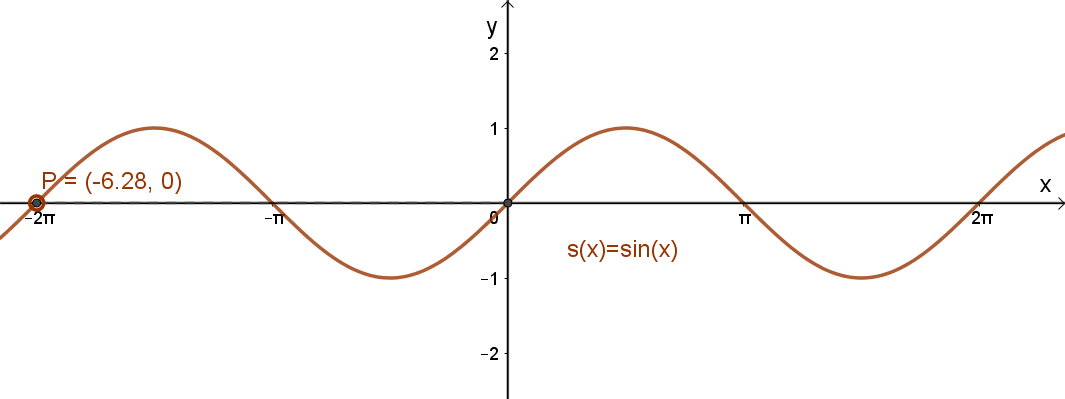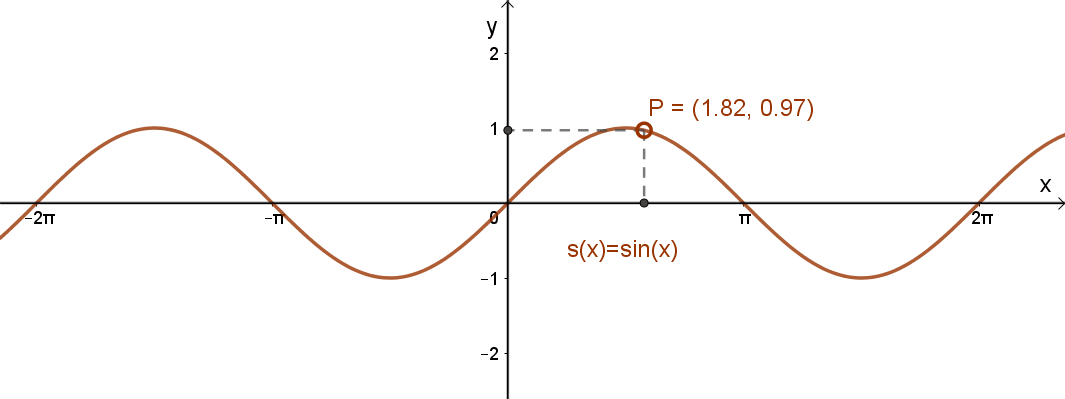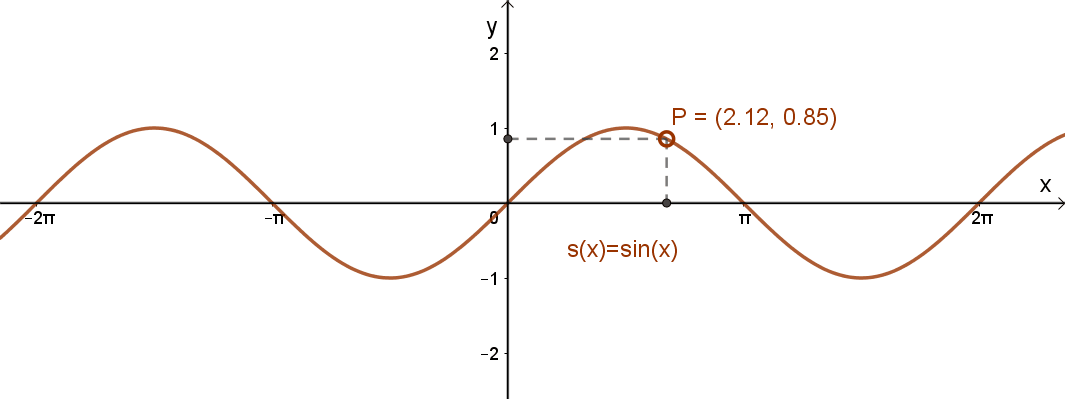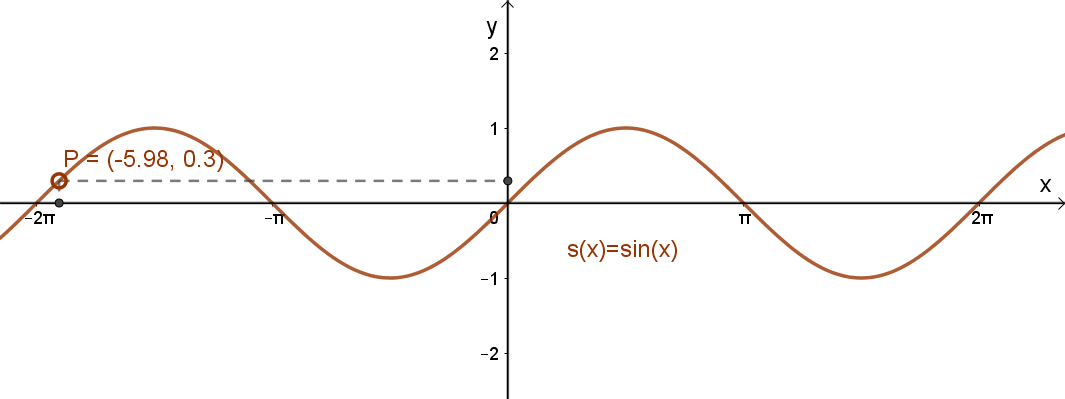
Az x→sin(x) függvény jellemzése:
| Értelmezési tartomány: | x∈ℝ. |
| Értékkészlet: | y=sin(x)∈ℝ|y∈[-1;1] |
| Zérushelye: | x=0+kπ ; k∈ℤ. |
| Menete: | Monoton nő, ha -π/2+k2π≤x≤π/2+k2π; k∈ℤ. Monoton csökken, ha π/2+k2π≤x≤3π/2+k2π; k∈ℤ. |
| Szélsőértéke: | Maximum: y=1; x=π/2+k2π; k∈ℤ. Minimum: y=-1; x= 3π/2+k2π; k∈ℤ. |
| Korlátos: | Igen. -1≤sin(x)≤+1 |
| Páros vagy páratlan: | Páratlan, sin(-x)=-sin(x) |
| Periodikus: | Igen. A periódus hossza: p=2π. |
| Konvex/konkáv: | Konvex, ha π+k2π<x<2π+k2π; k∈ℤ és konkáv, ha 0+k2π<x<π+k2π; k∈ℤ |
| Folytonos: | Igen. |
| Inverz függvénye: | Van: f-1(x)=arcsin(x), ha -1≤x≤1. |
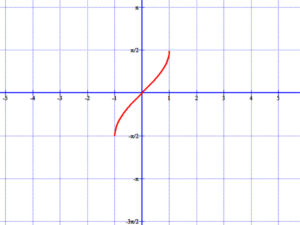
Szinusz függvény inverze az f-1(x)=arcsin(x):
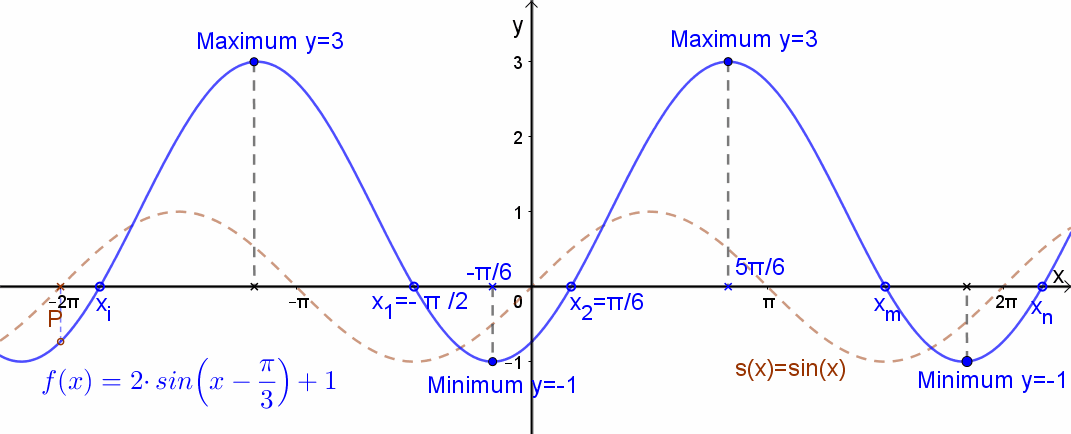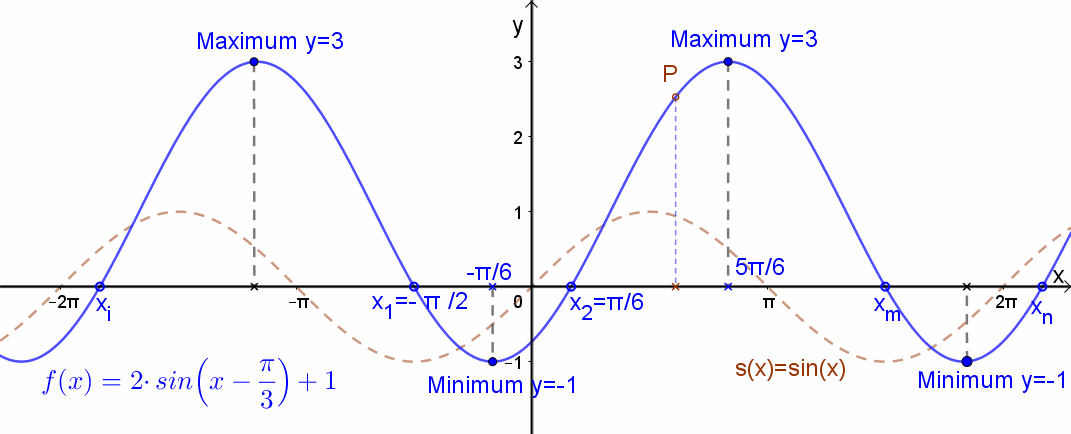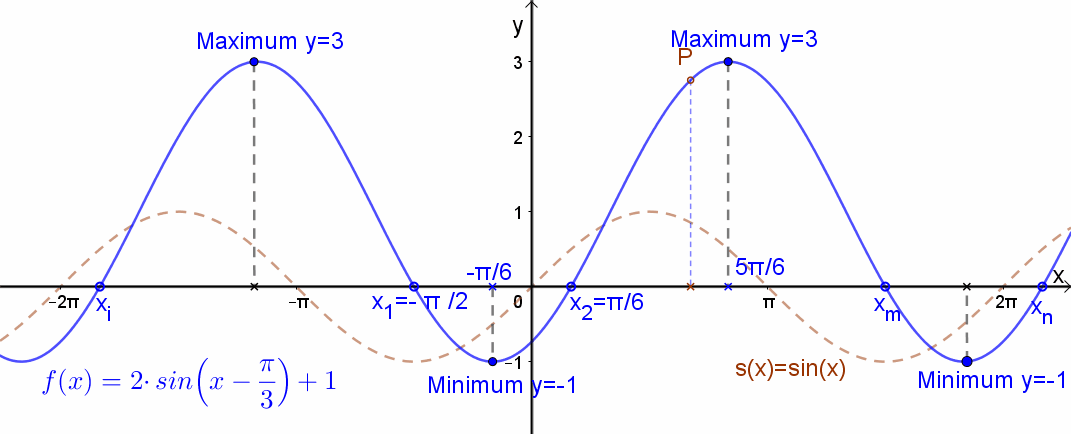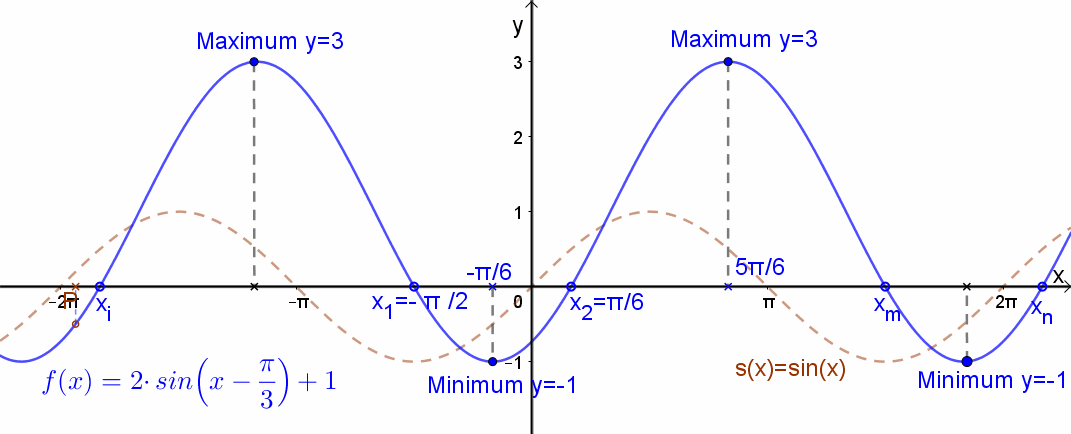
Ábrázoljuk most függvénytranszformációk segítségével az f(x)=2⋅sin(x-π/3)+1 függvényt.
Ez az eredeti függvényhely képest el van tolva az „x” tengely mentén jobbra π/3-mal , meg van nyújtva az „y” tengely mentén és el van tolva felfelé 1 egységgel.
A függvény grafikonja:


Comments are closed, but trackbacks and pingbacks are open.