Az \( x→\sqrt[n]{x} \) függvények ábrázolása és jellemzése.
Gyökfüggvények tárgyalásánál alapvetően két esetet kell megkülönböztetni attól függően, hogy a gyökkitevő páros avagy páratlan (2-nél nem kisebb) pozitív egész szám.
Az alábbi grafikonok ennek megfelelően mutatják a \( x→\sqrt{x} \) és a \( x→\sqrt[3]{x} \) függvények grafikonjait.
Függvény grafikonok:
| \( x→\sqrt{x} \) | \( x→\sqrt[3]{x} \) |
|
|
|
Gyökfüggvények jellemzése:
A gyökfüggvények jellemzésénél bizonyos függvényvizsgálati szempontok függetlenek a gyökkitevő típusától, de vannak olyan szempontok is, amelyeknél a függvényvizsgálati válasz attól függ, hogy páros vagy páratlan a gyökkitevő.
Az alábbi táblázat ennek megfelelően csoportosítva tartalmazza a gyökfüggvények jellemzését.
|
Páros gyökkitevő |
Tetszőleges gyökkitevő |
Páratlan gyökkitevő |
|
| Értelmezési tartomány: | Nemnegatív valós számok halmaza: x∈ℝ|x≥0. | Valós számok halmaza: x∈ℝ. | |
| Értékkészlet: | Nemnegatív valós számok halmaza: y∈ℝ|y≥0 |
Valós számok halmaza: y∈ℝ | |
| Zérushelye: | x=0 | ||
| Menete: | Szigorúan monoton nő. | ||
| Szélsőértéke: | Minimum: | Nincs. | |
| Korlátos: | Alulról korlátos, felülről nem. Alsó korlát k=0 |
Nem. | |
| Páros vagy páratlan: | Egyik sem | Páratlan. | |
| Periodikus: | Nem. | ||
| Konvex/konkáv: | Konkáv. | Konvex, ha x<0 és konkáv, ha x>0 | |
| Folytonos: | Igen. | ||
| Inverz függvénye: | Az \( x→x^{n} \) hatványfüggvény az értelmezési tartományuk metszetén.. |
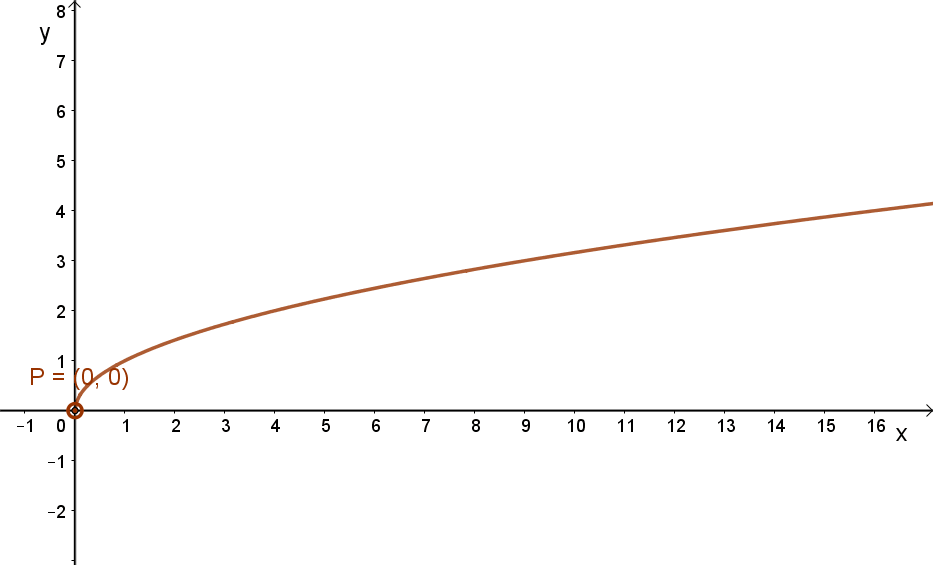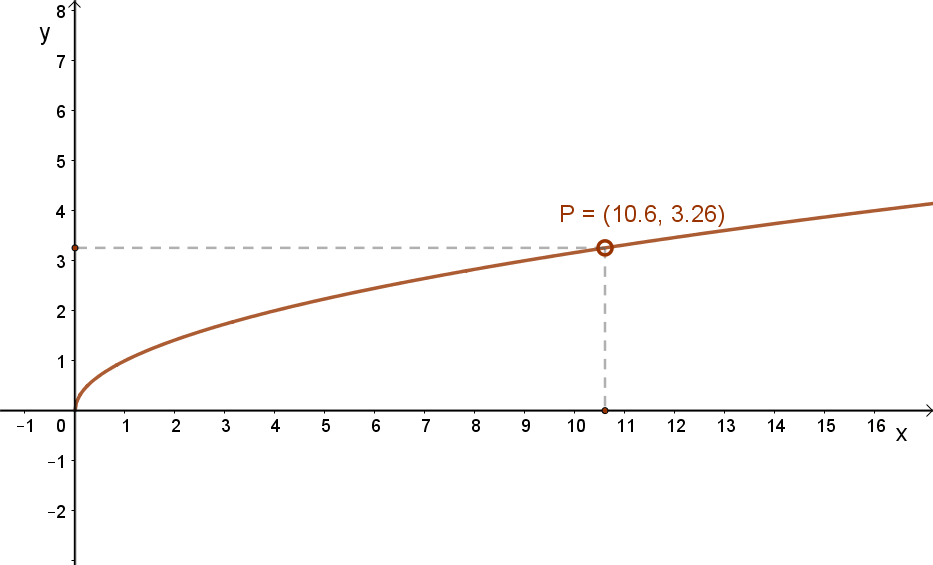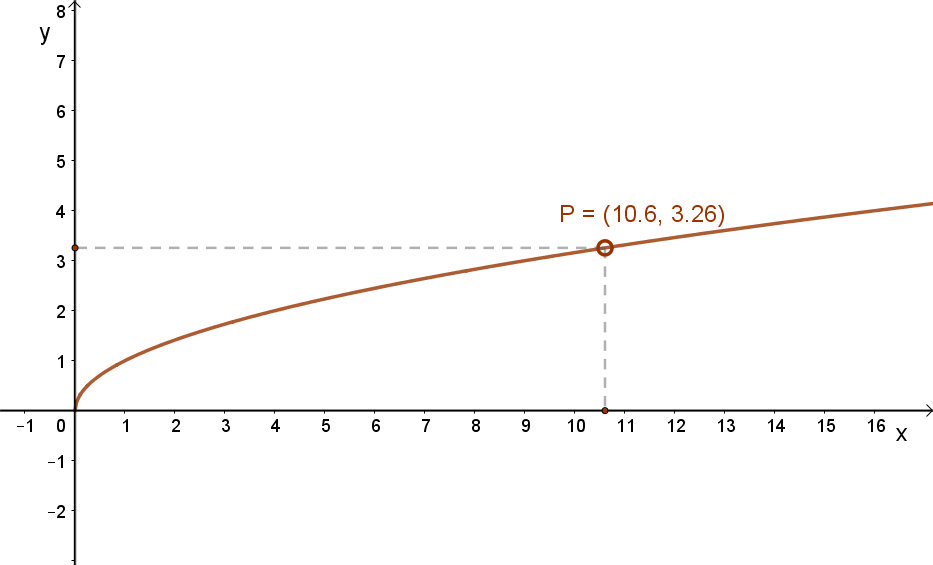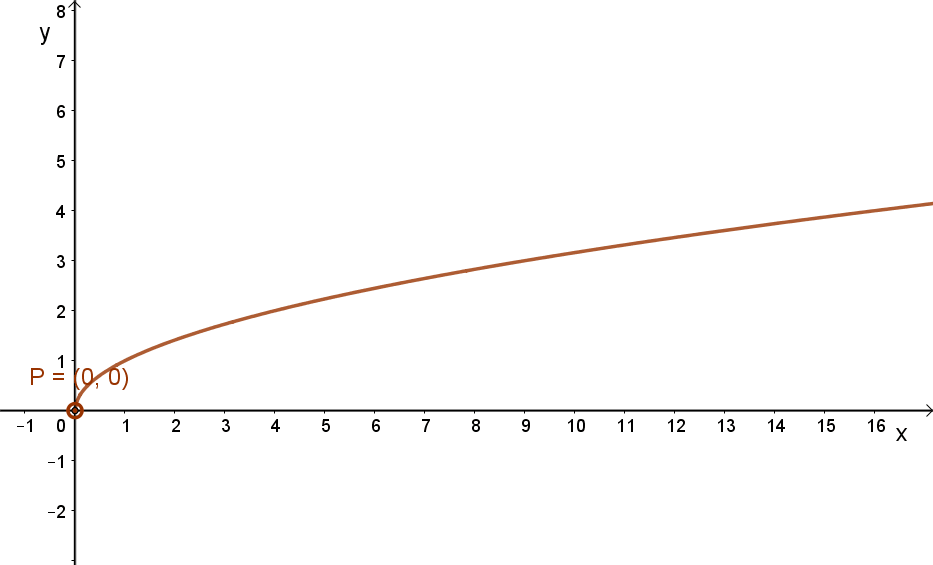
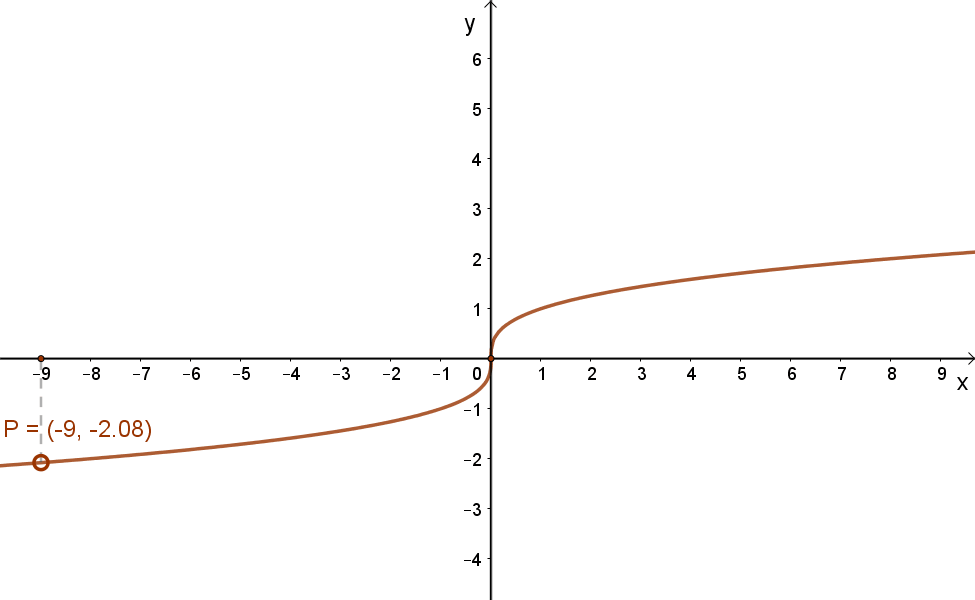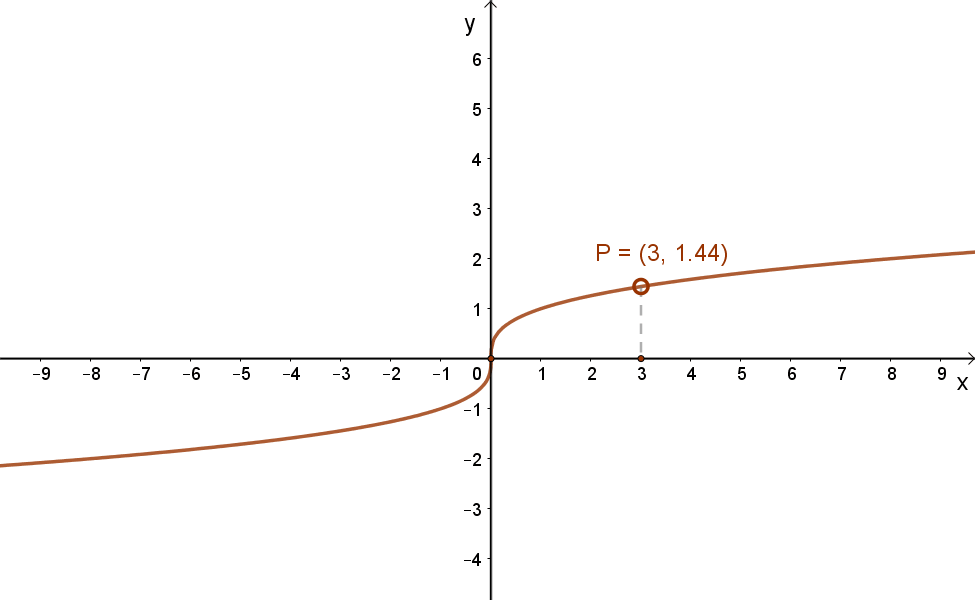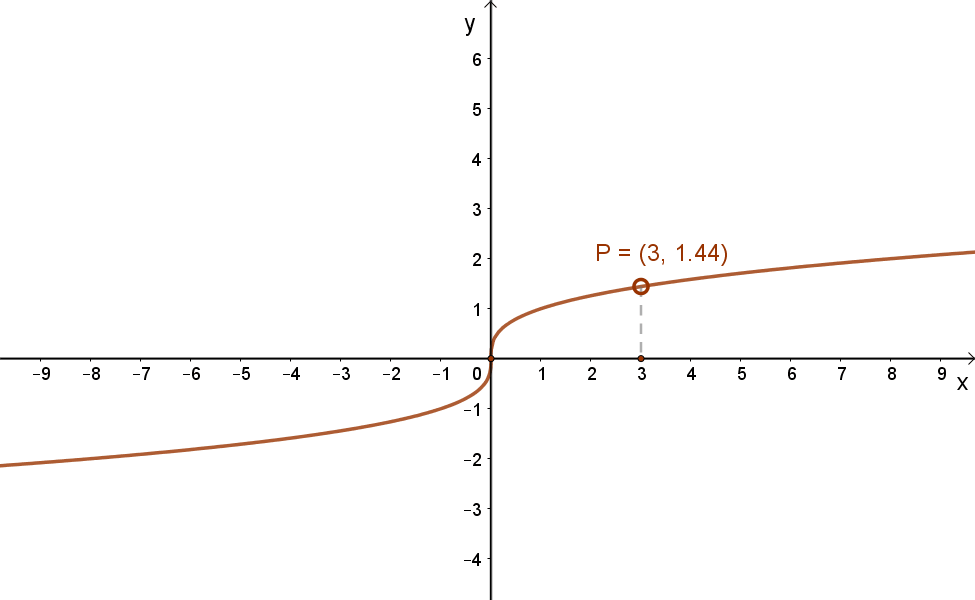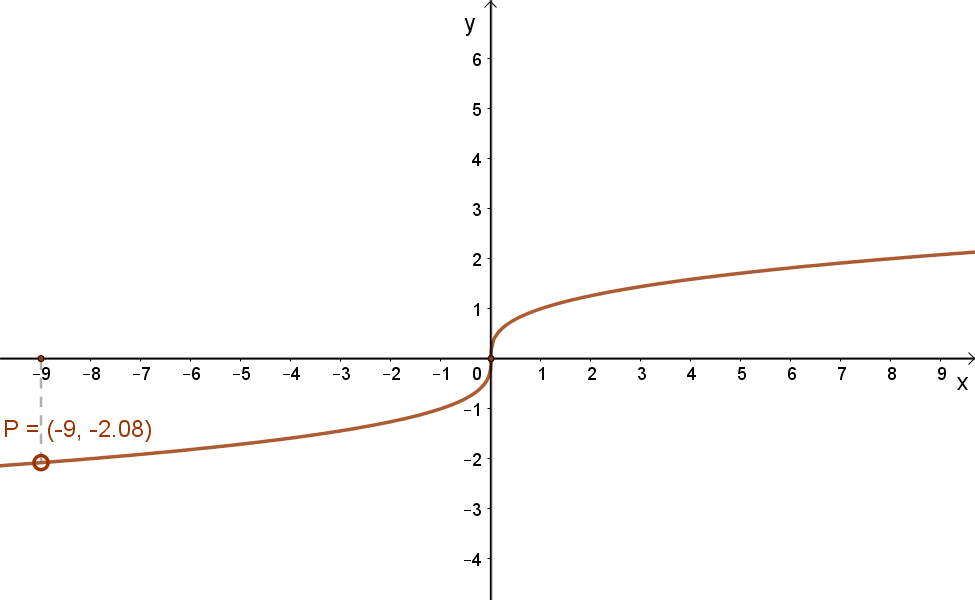


Comments are closed, but trackbacks and pingbacks are open.