Függvény párossága.
Definíció:
Az f:H→ℝ, x→ f(x) függvényt párosnak nevezzük, ha az értelmezési tartomány minden x elemével együtt -x is a függvény értelmezési tartományához tartozik és az értelmezési tartomány bármely x eleme esetén f(-x)=f(x).
Ellentett helyen megegyező függvényértéket kapunk.
A páros függvények képe szimmetrikus a koordinátasík y tengelyére.
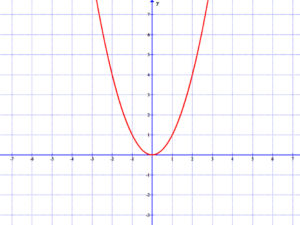
Páros függvény például az m(x)=x2 másodfokú függvény, hiszen m(-3)=(-3)2=9 és m(3)=32=9. A másodfokú függvény grafikonja:
További példák páros függvényekre: a páros kitevőjű hatvány függvények (alaphelyzetben), az abszolút érték függvény.
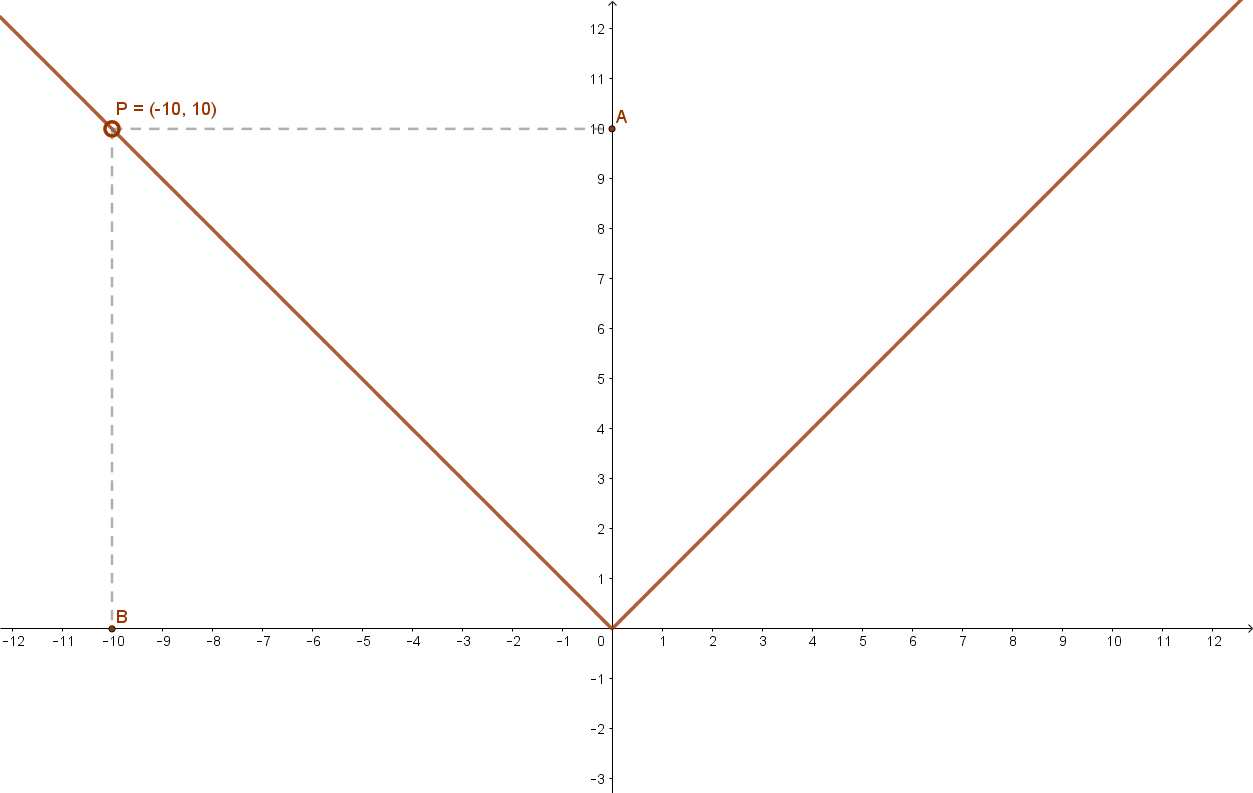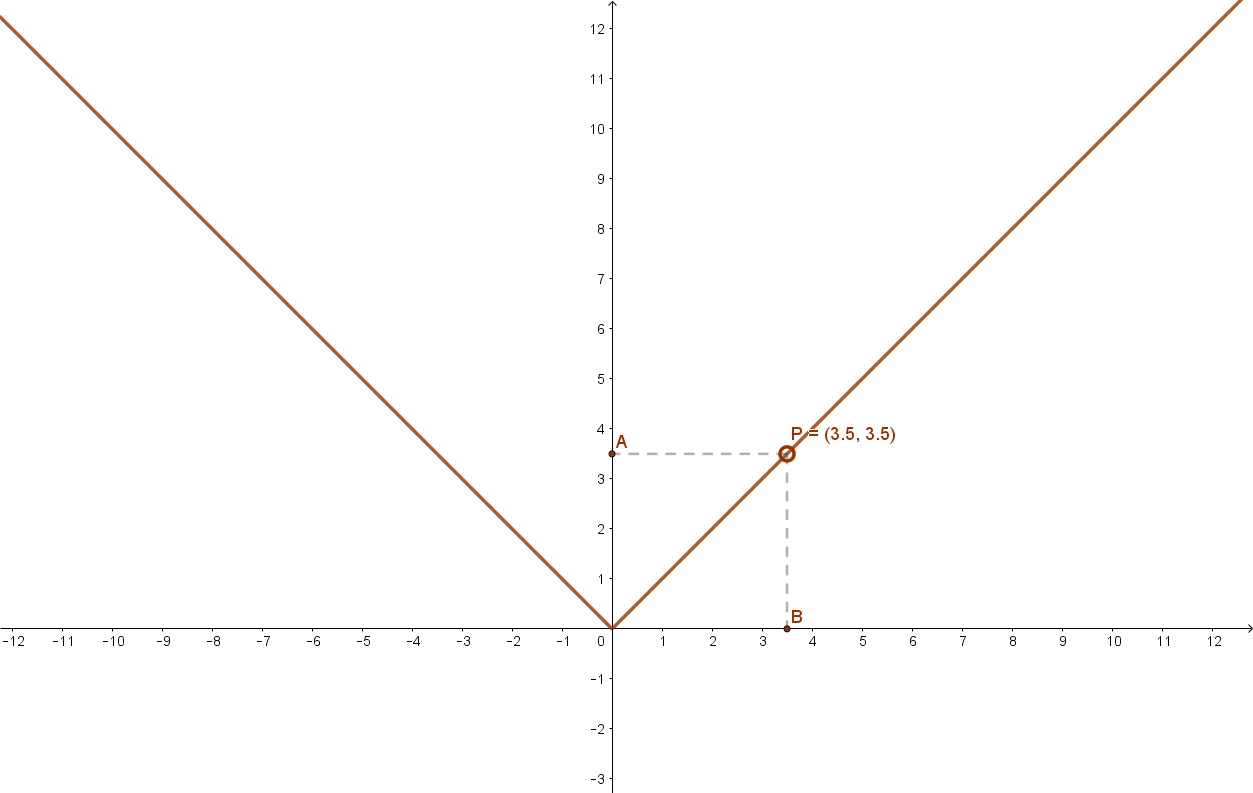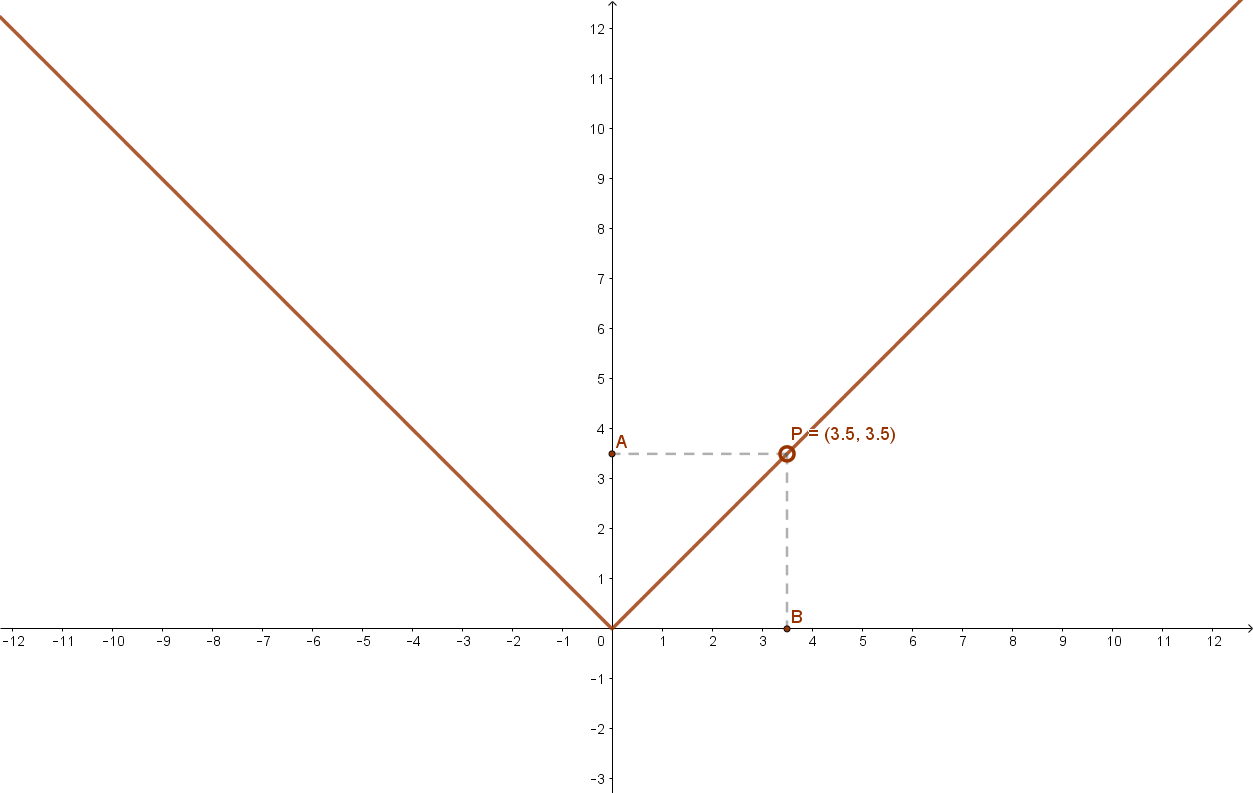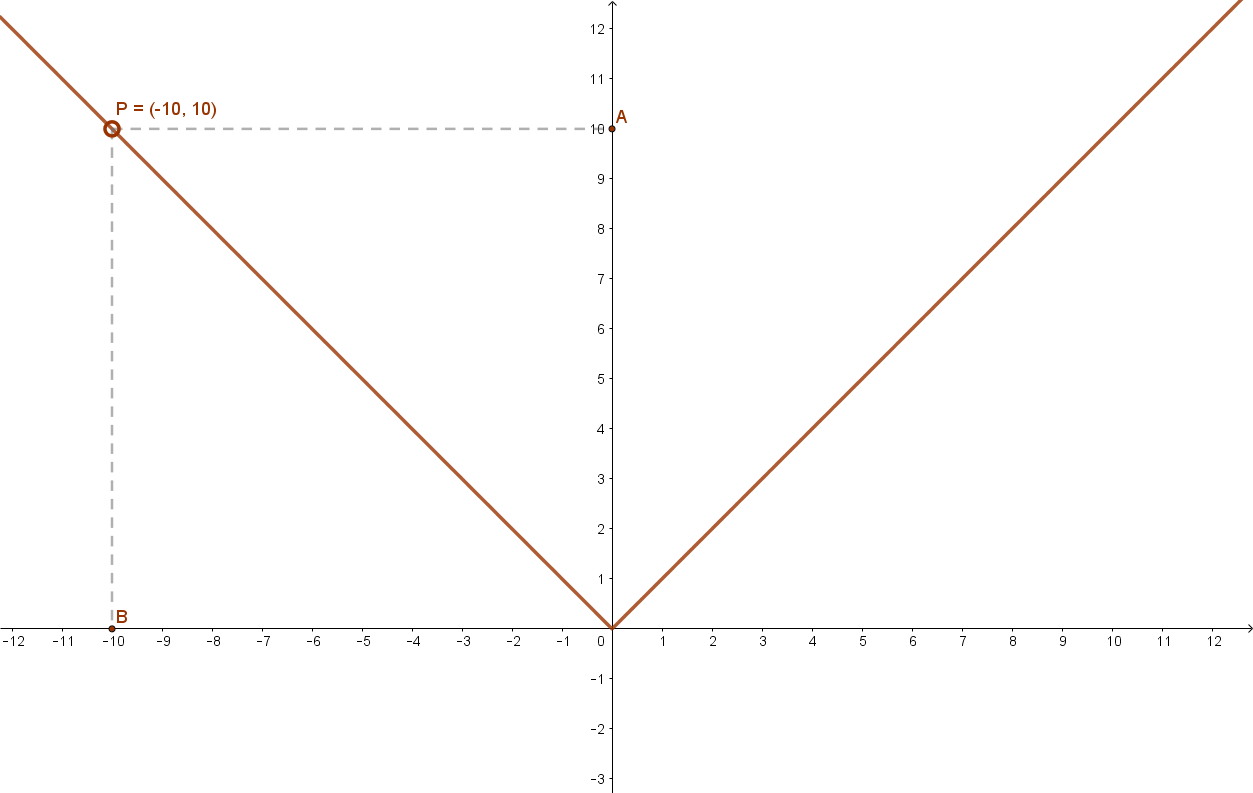
Ugyancsak páros függvény a koszinusz függvény is.
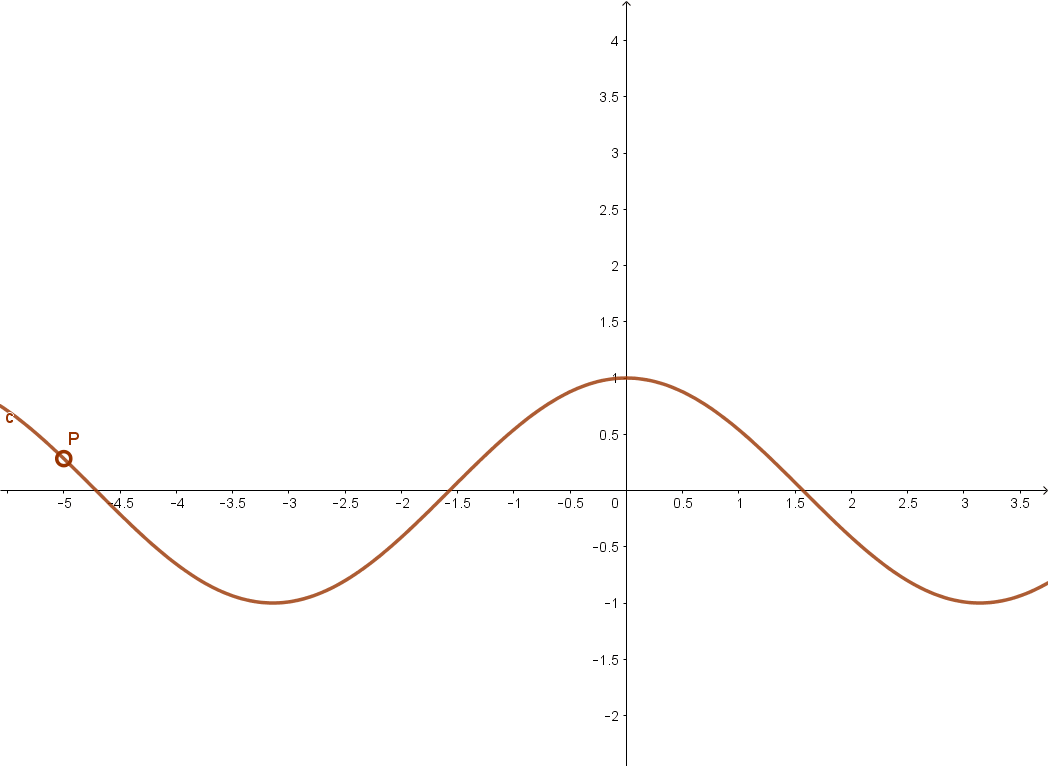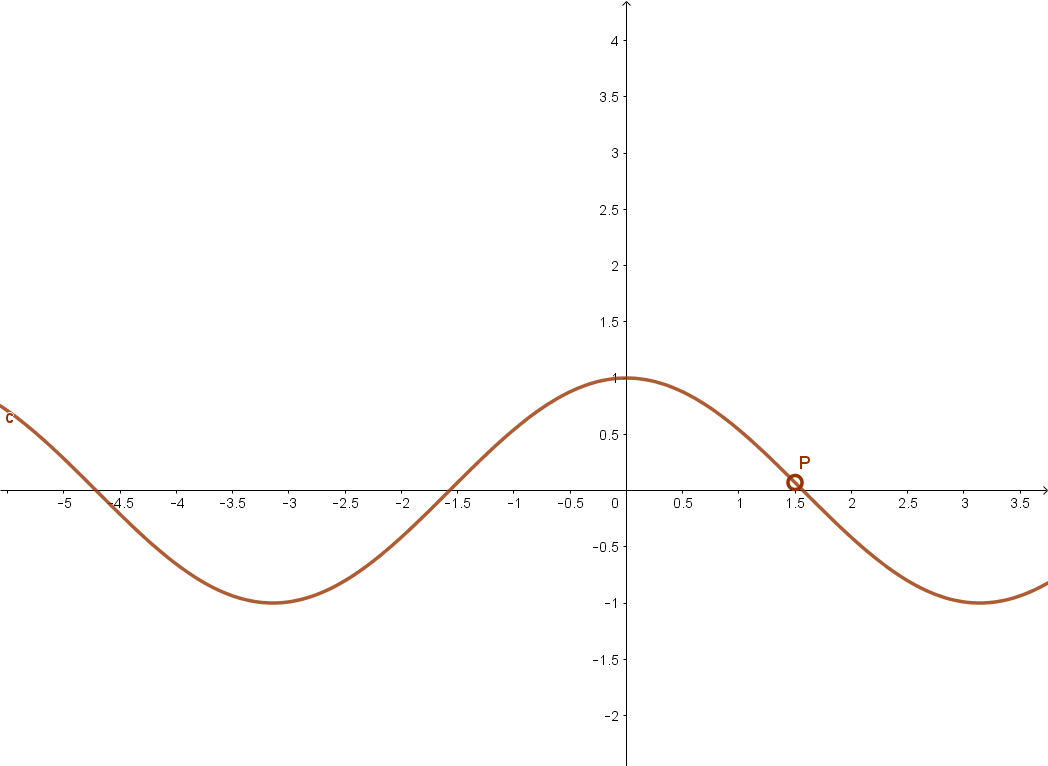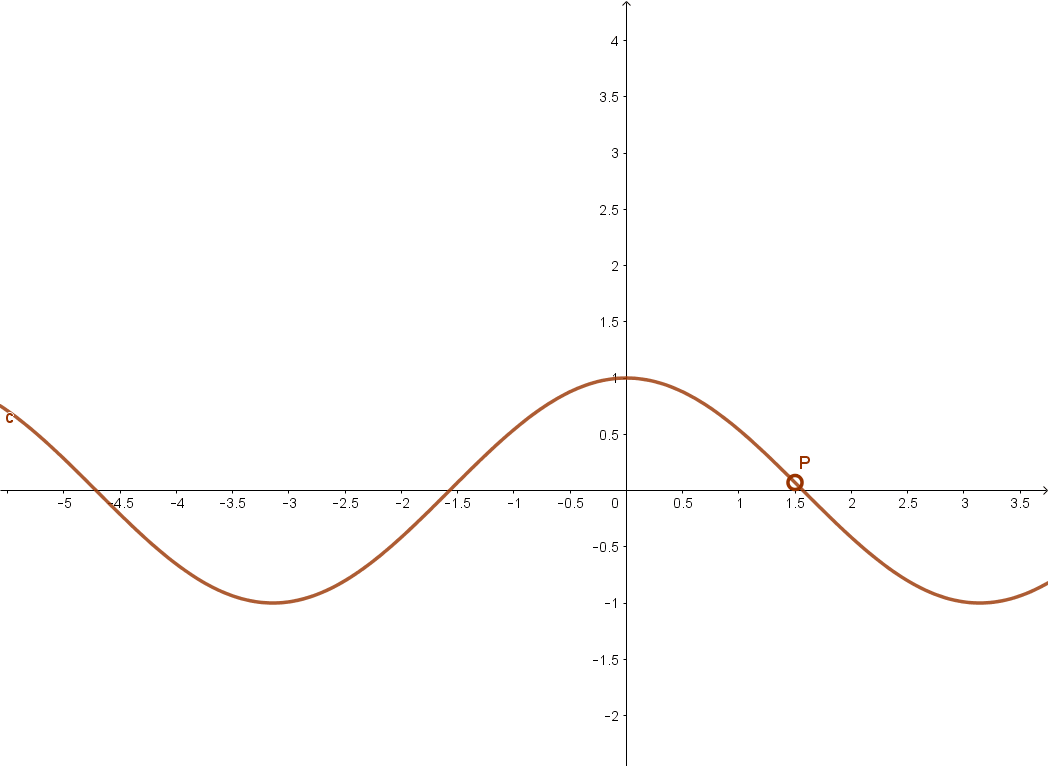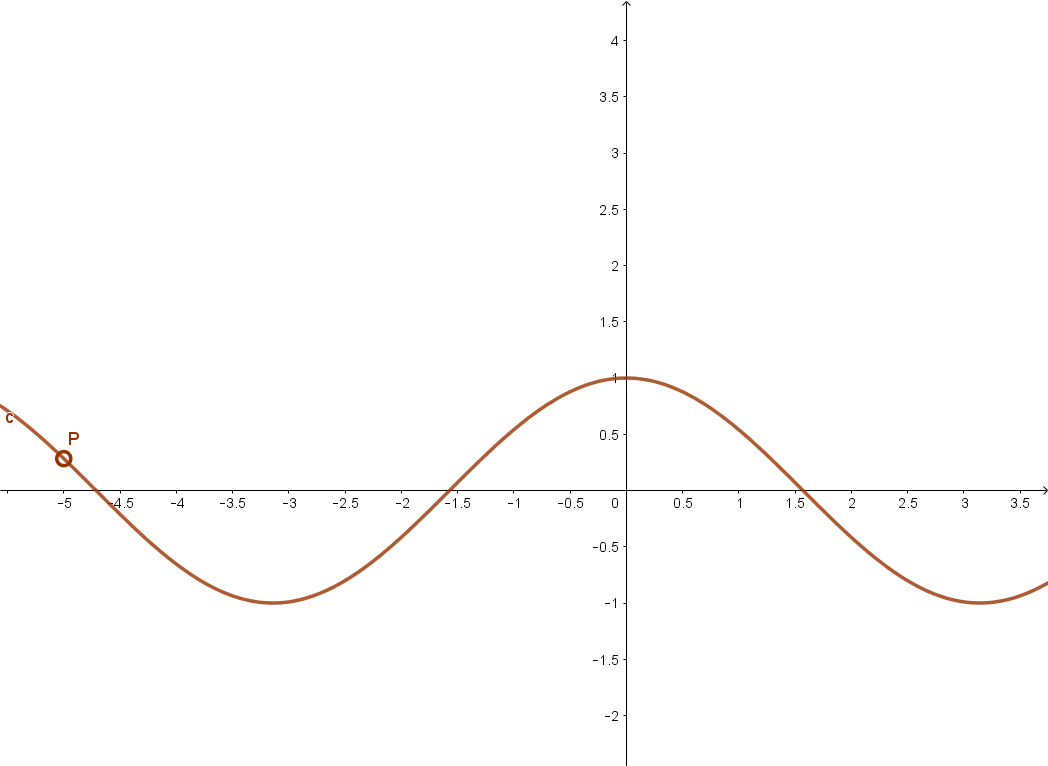
Függvény páratlansága.
Definíció:
Az f:H→ℝ, x→ f(x)) függvényt páratlannak nevezzük, ha az értelmezési tartomány minden x elemével együtt -x is a függvény értelmezési tartományához tartozik, és az értelmezési tartomány bármely x eleme esetén f(-x)=-f(x).
Ellentett helyen ellentett függvényértéket kapunk.
A páratlan függvények képe szimmetrikus a koordinátasík kezdőpontjára (az origóra).
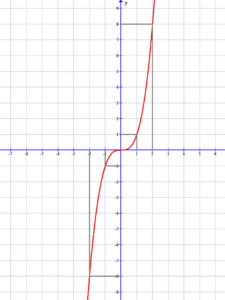
Páratlan függvény például a h(x)=x3 harmadfokú függvény, hiszen h(-2)=(-2)3=-8, és h(2)=23=8.
Az egyenes és a fordított arányosság függvénye, a páratlan kitevőjű hatvány függvények.
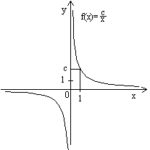
A fordított arányosság függvénye: f(x)=c/x.
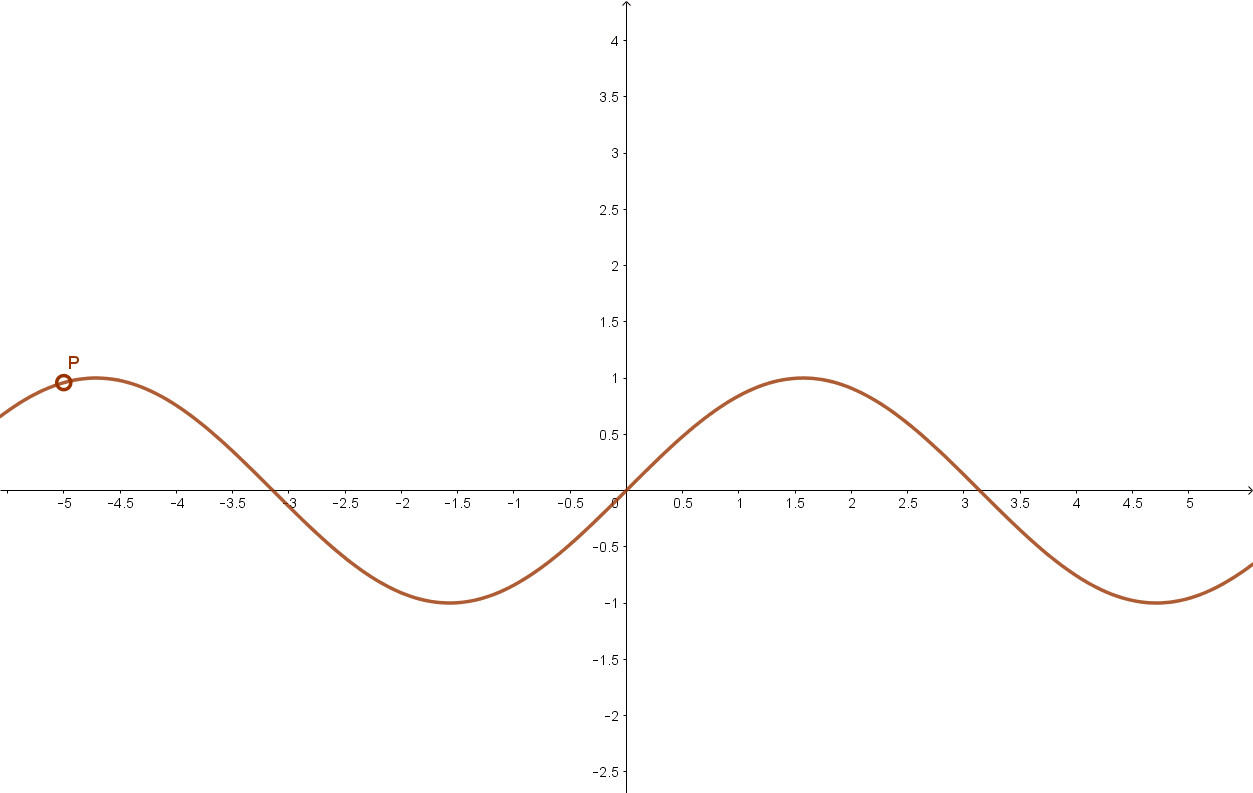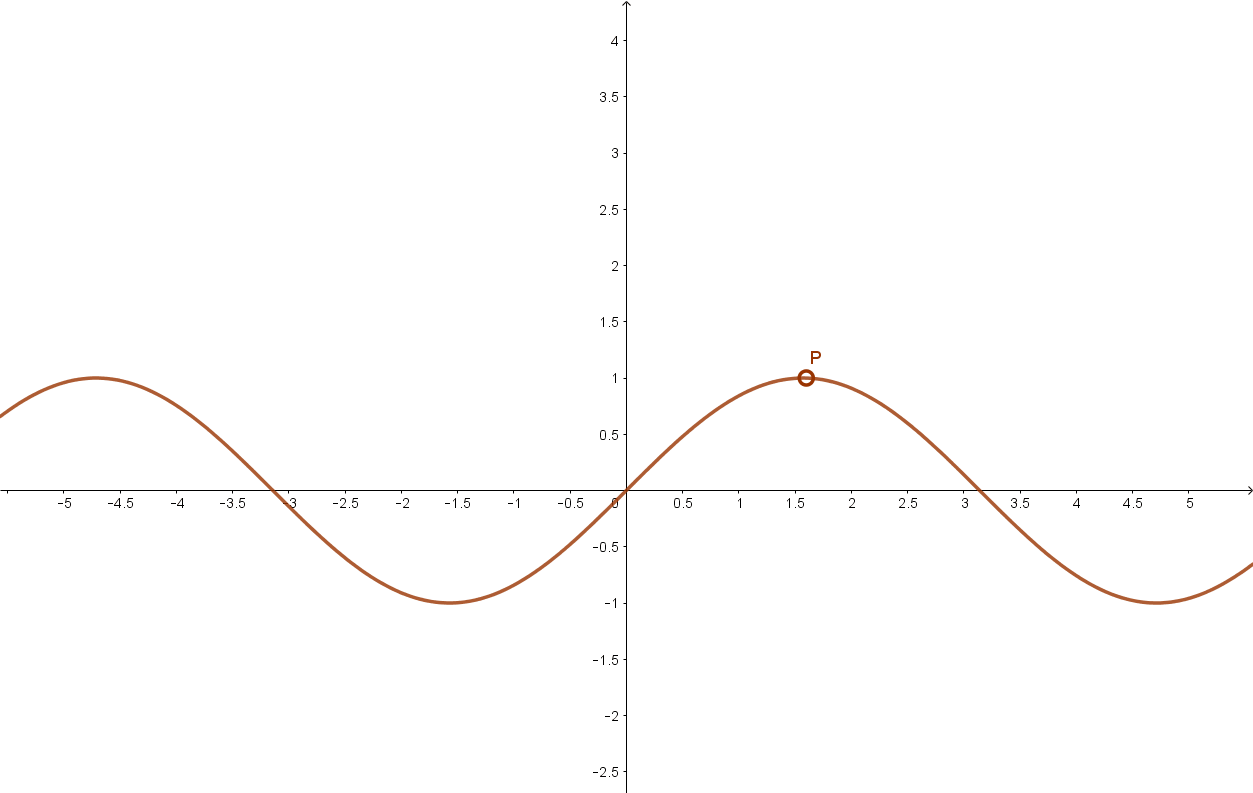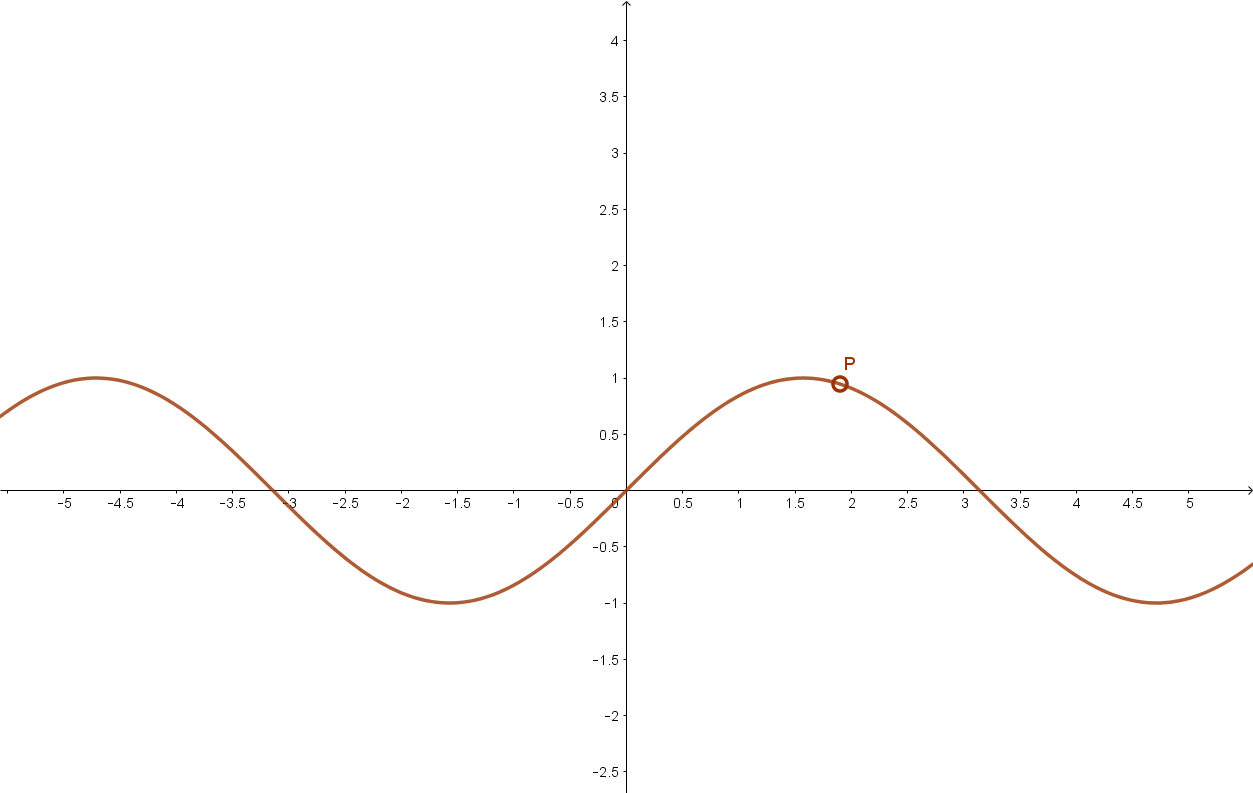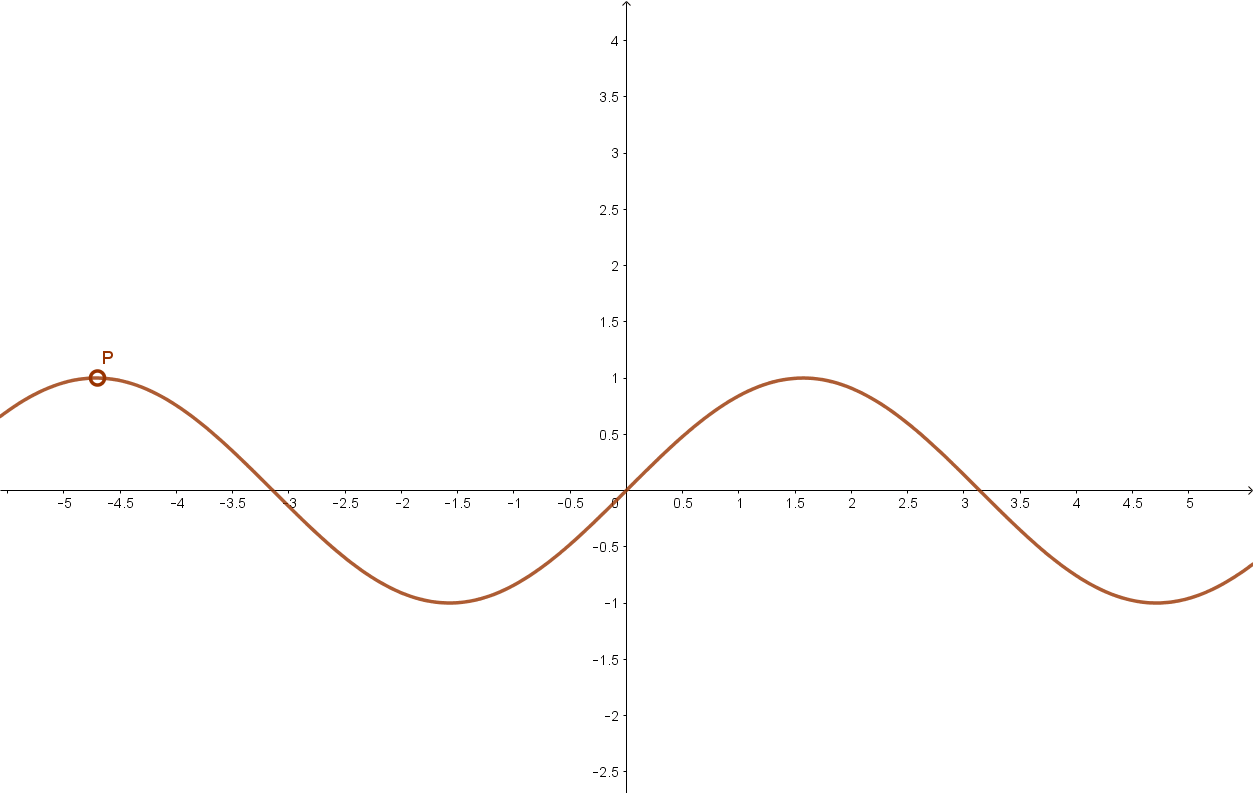


Comments are closed, but trackbacks and pingbacks are open.