Függvények monotonitása

Definíció:

Az f:H→ℝ​, x→ f(x) függvény egy [a;b] intervallumban monoton nő, ha ott értelmezve van és az intervallum minden olyan pontjára, amelyre x₁<x₂, akkor f(x₁)≤(x₂).

(Röviden úgy is mondhatjuk, hogy nagyobb változóhoz nagyobb vagy egyenlő függvényérték tartozik.

Példa:

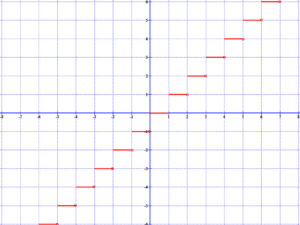
A monoton növekedő függvényre jó példa az un. egészrész függvény, amelynek a képzési szabálya a következő:
e:ℝ→ℝ​, x→[x], ahol [x] az a legnagyobb egész szám, amely még nem nagyobb, mint az x. A függvény értéke például az x=1,2 helyen: e(1,2)=1, és a függvény értéke az x=-1,2 helyen e(-1,2)=-2, mert -2 az a legnagyobb egész szám, amely még nem nagyobb, mint a -1,2.

Ez a függvény a teljes értelmezési tartományon monoton nő.

Megjegyzés: A monoton növekedés mellett használjuk a szigorúan monoton növekedés fogalmát, amikor nagyobb változóhoz nagyobb függvényérték tartozik.

Definíció:

Az f:H→ℝ​, x→ f(x) függvény egy [a;b] intervallumban szigorúan monoton nő, ha ott értelmezve van és az intervallum minden olyan pontjára, amelyre x₁<x₂, akkor f(x₁)<(x₂).

Példa:

Szigorúan monoton növekszik a szinusz függvény például a ​\( \left [ -\frac{ π }{2};+\frac{π}{2} \right ] \)​ intervallumon.

 

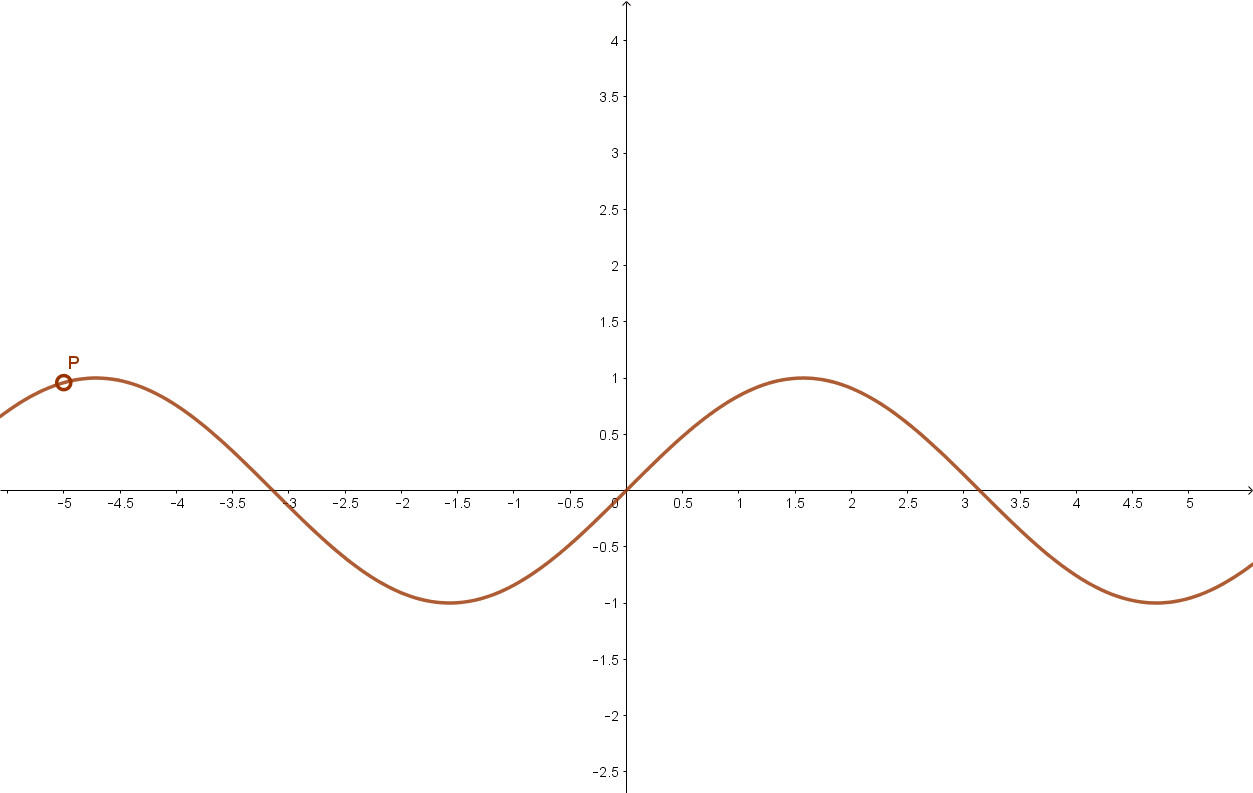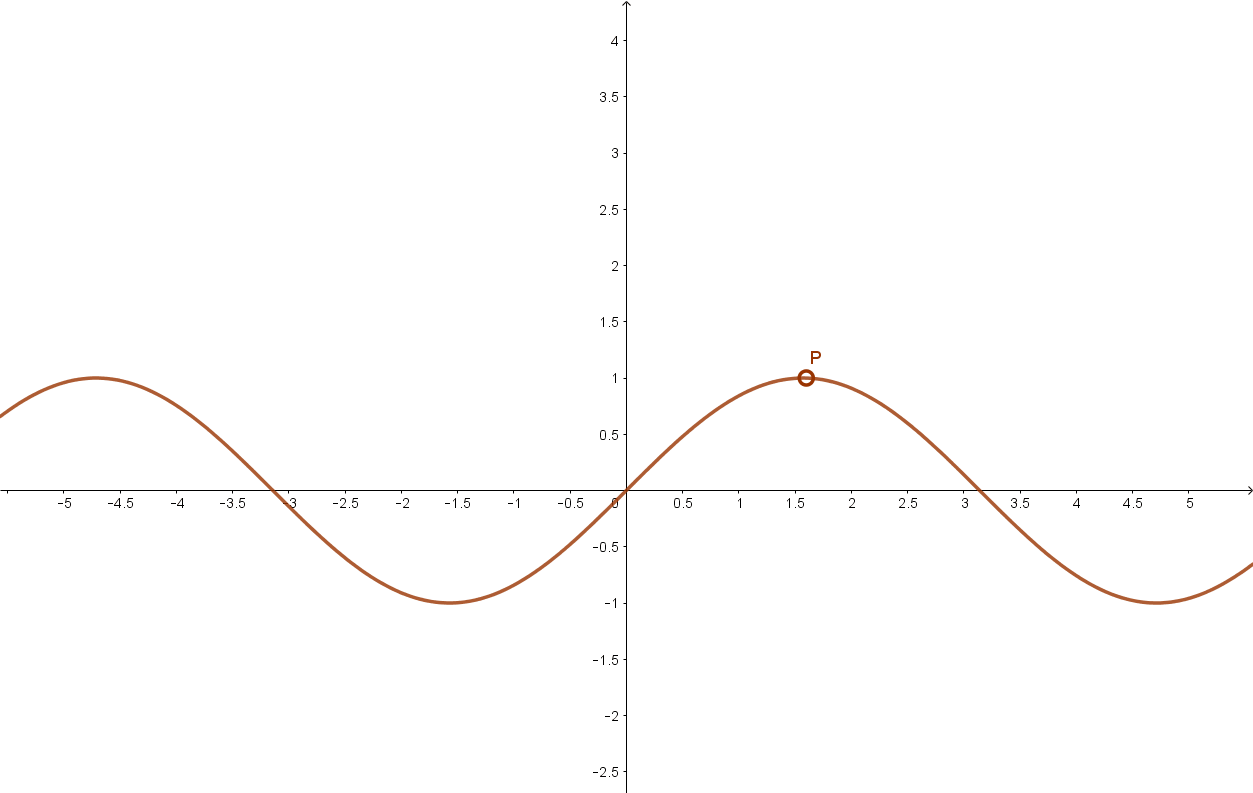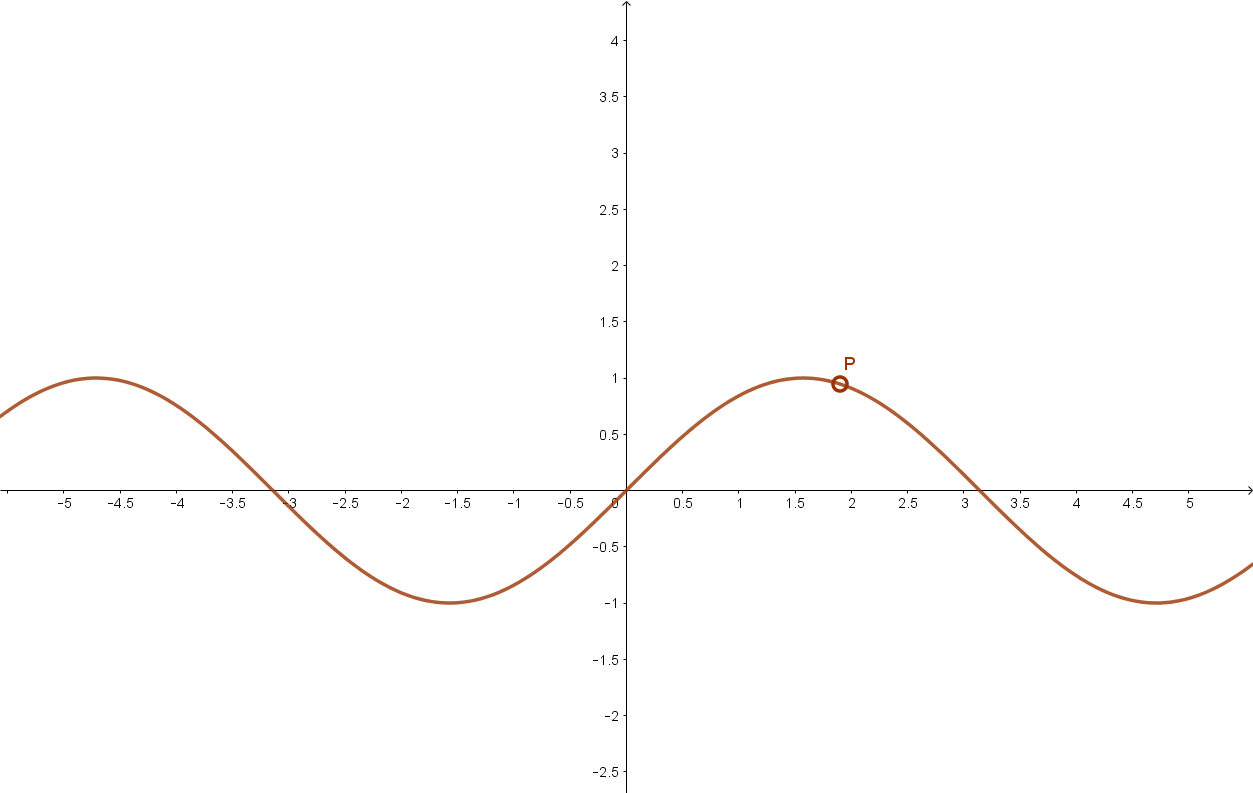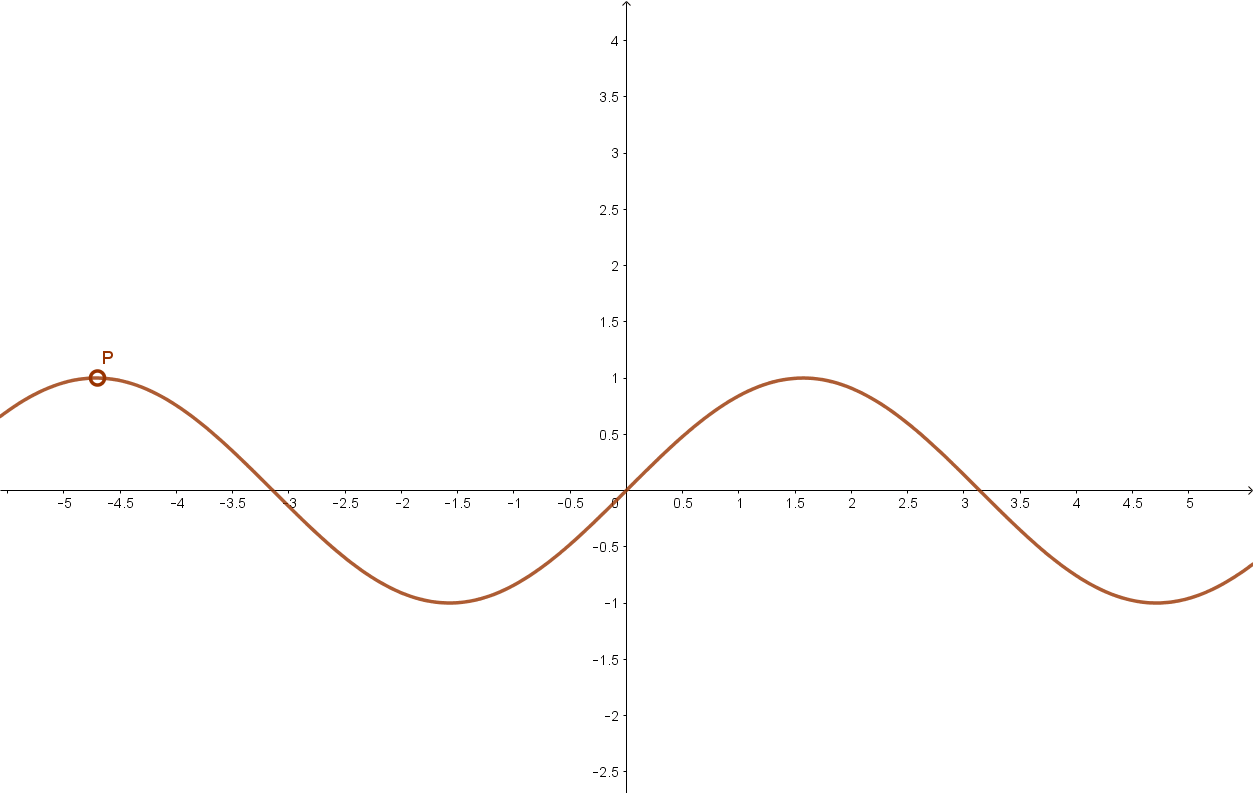
Definíció:

Az f:ℝ→ℝ​, x→ f(x) függvény egy [a;b] intervallumban monoton csökken, ha ott értelmezve van és az intervallum minden olyan pontjára, amelyre x₁<x₂, akkor f(x₁)≥(x2).

(Röviden úgy is mondhatjuk, hogy nagyobb változóhoz kisebb vagy egyenlő függvényérték tartozik. (Megfordul a relációs jel)

Megjegyzés: A monoton csökkenés mellett használjuk a szigorúan monoton csökkenés fogalmát, amikor nagyobb változóhoz kisebb függvényérték tartozik. Ebben az esetben nem engedjük meg tehát az egyenlőséget.

Definíció:

Az f:ℝ→ℝ​, x→ f(x) függvény egy [a;b] intervallumban szigorúan monoton csökken, ha ott értelmezve van és az intervallum minden olyan pontjára, amelyre x₁<x₂, akkor f(x₁)>(x₂).

Példa:

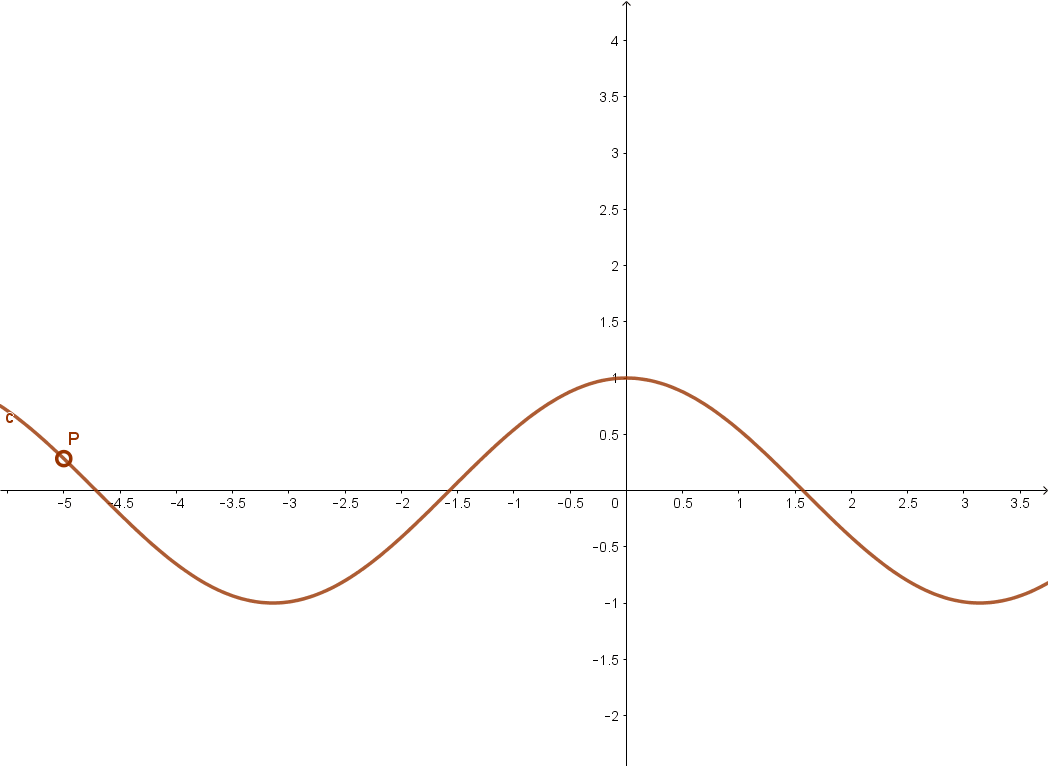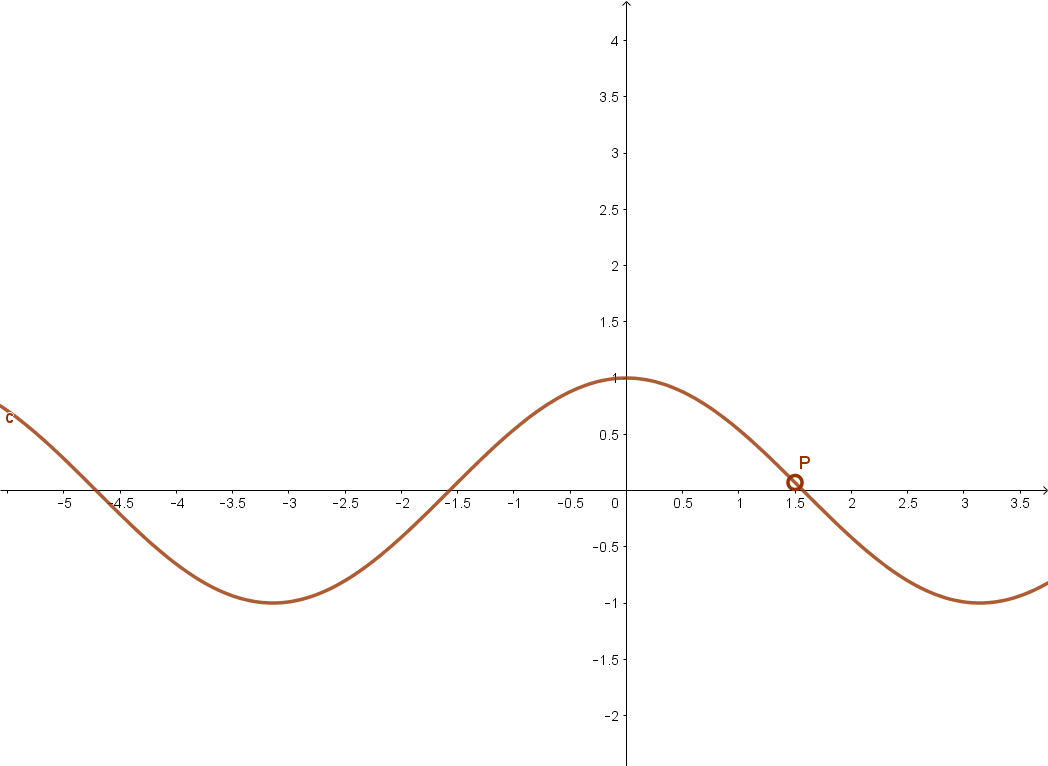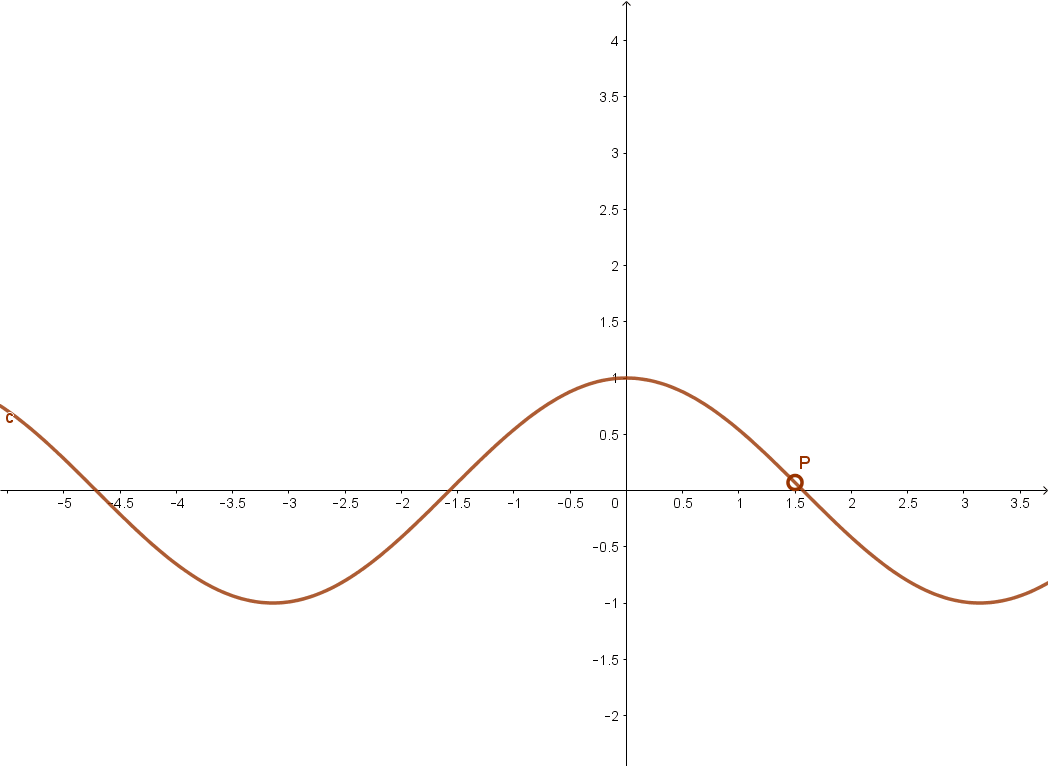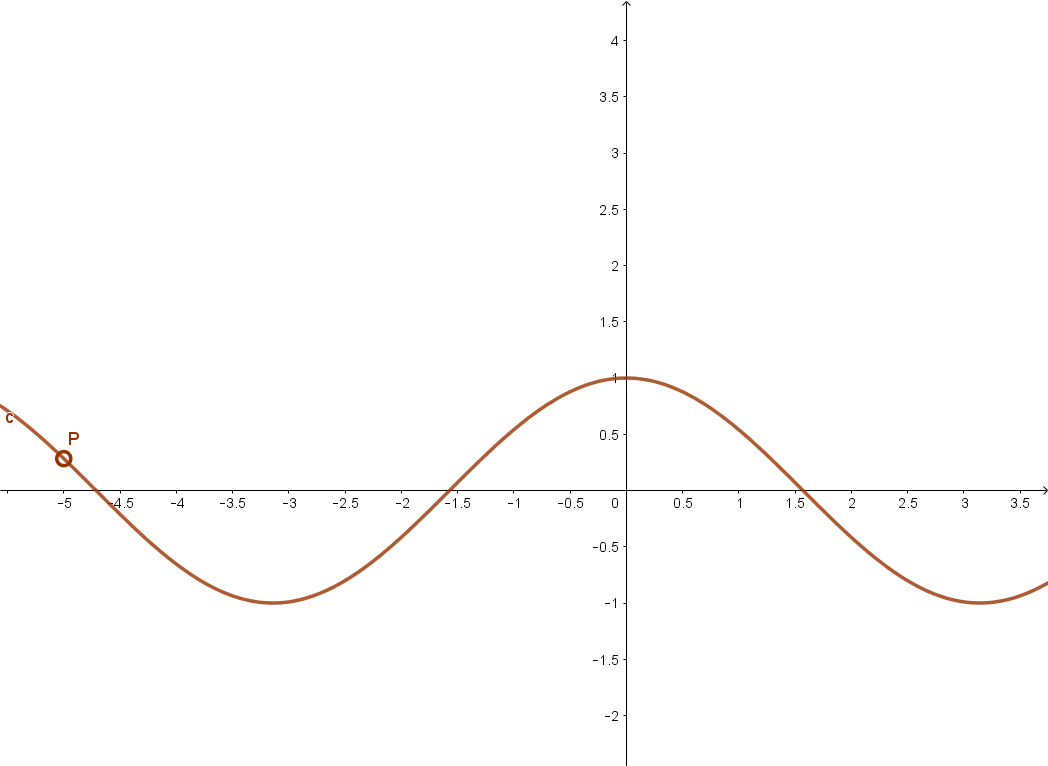
Szigorúan monoton csökken a koszinusz függvény például a [0; π ] intervallumon.

Vizsgáljuk meg most a következő függvény menetét:  ​\( f(x)=\frac{1}{x-3}+2=\frac{2x-5}{x-3} \)​.