Középiskolában függvényeket a következő szempontok szerint vizsgáljuk.
Függvény értelmezési tartománya:
A függvény változóinak halmaza, amelyekhez lett függvényérték rendelve. (Jele „g” nevű függvény esetén: Dg.)
Példa:
A mellékelt g: ℝ→ℝ, \( g(x)=2\sqrt{x-4}-3 \) függvény esetén: Dg=ℝ\{x<4}. Másképp: Értelmezési tartomány: x∈ℝ|x≥4. Az értelmezési tartományt az ábrázolható függvények esetén a”x” (változó) tengely mutatja.
Függvény értékkészlete:
Képhalmaznak a függvény helyettesítési értékeit tartalmazó részét a függvény értékkészletének nevezzük. (Jele „g” nevű függvény esetén: Rg.) A fenti, mellékelt g: ℝ→ℝ, \( g(x)=2\sqrt{x-4}-3 \) függvény esetén: Rg=ℝ\{y<(-3)}. Másképp: y∈ℝ|y≥-3. Az értékkészletet az ábrázolható függvények esetén a”y” (érték) tengely mutatja.
Függvény zérushelye:
Az g: ℝ→ℝ, \( g(x)=2\sqrt{x-4}-3 \) függvény zérus helyeinek nevezzük a Dg értelmezési tartomány mindazon x értékeit, amelyeknél a függvény értéke nulla, azaz g(x)=0. A zérus hely meghatározása tehát az g(x)=0 egyenlet megoldását igényli.
A fenti példa esetén: \( 2\sqrt{x-4}-3=0 \) Ennek megoldása: x=6,25.
Ábrázolható függvények esetén a zérus hely az a pont, ahol a függvény grafikonja metszi az „x” tengelyt.
Függvény menete, monotonitása:
Az f(x) függvény értelmezési tartományának [a; b] intervallumában monoton növekedőnek (fogyónak) mondjuk, ha bármely x1∈[a; b] és x2∈[a; b] és x1<x2 f(x1)≤ f(x2) (illetve f(x1)≥f(x2)) relációk teljesülése esetén monoton növekedésről (illetve csökkenésről) beszélünk. Az f(x1)<f(x2) (illetve f(x1)> f(x2)) relációk teljesülése esetén szigorúan monoton növekedésről (illetve csökkenésről) beszélünk.
Például:
A mellékelt f: ℝ→ℝ, f(x)=(x+3)2-4 másodfokú függvény szigorúan monoton csökken a )-∞;-3) intervallumon éa szigorúan monoton nő a (-3; +∞) intervallumon.
Szélsőérték:
Az f(x) függvénynek x0∈Df pontban (globális) maximuma (illetve minimuma) van, ha minden x∈Df-re f(x) ≤ f(x0) (illetve f(x) ≥ f(x0) minimum esetén).
Az f(x) függvénynek x0∈Df pontban helyi (lokális) maximuma (illetve helyi minimuma) van, ha x0-nak van olyan δ>0 környezete, hogy minden az x0-δ≤x≤x0+δ egyenlőtlenséget kielégítő x pontban teljesül az f(x)≤f(x0) egyenlőtlenség. (illetve az f(x)≥ f(x0) helyi minimum esetén.)
Például:
A fenti f: ℝ→ℝ, f(x)=(x+3)2-4 másodfokú függvénynek globális minimuma van a (-3;-4) pontban.
Korlátosság:
Az f:ℝ→ℝ, x→f(x) függvény alulról korlátos, ha van olyan k valós szám, hogy az értelmezési tartomány minden elemére k≤ f(x).
Az f(x) függvény felülről korlátos, ha van olyan K valós szám, hogy az értelmezési tartomány minden elemére f(x)≤K.
Az f(x) függvény korlátos, ha alulról és felülről is korlátos, azaz van olyan k; K valós szám, hogy az értelmezési tartomány minden elemére k≤f(x)≤K.
Például:
A fenti f: ℝ→ℝ, f(x)=(x+3)2-4 másodfokú függvény alulról korlátos, hiszen tetszőleges x esetén f(x)≥-4.
Függvény párossága, páratlansága (Paritása):
Definíció: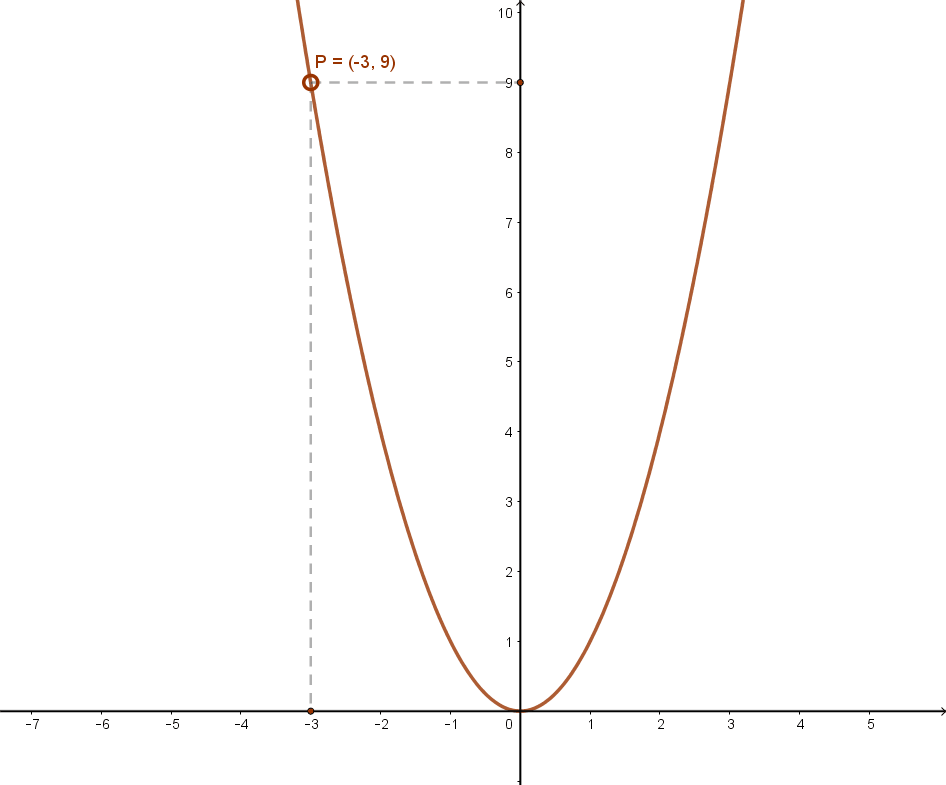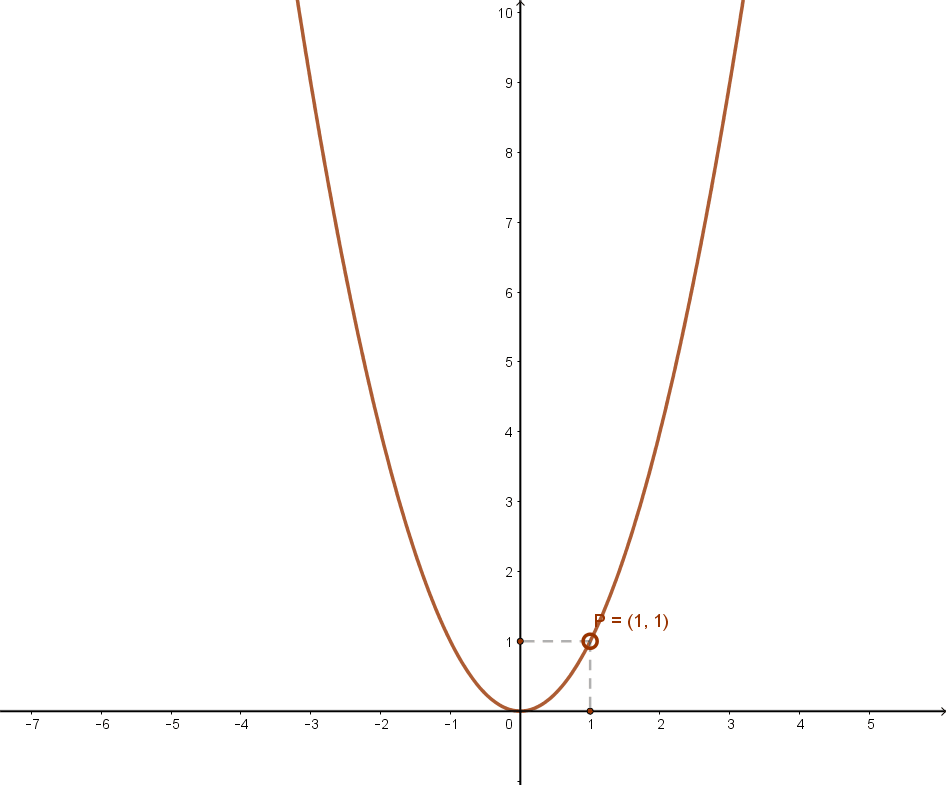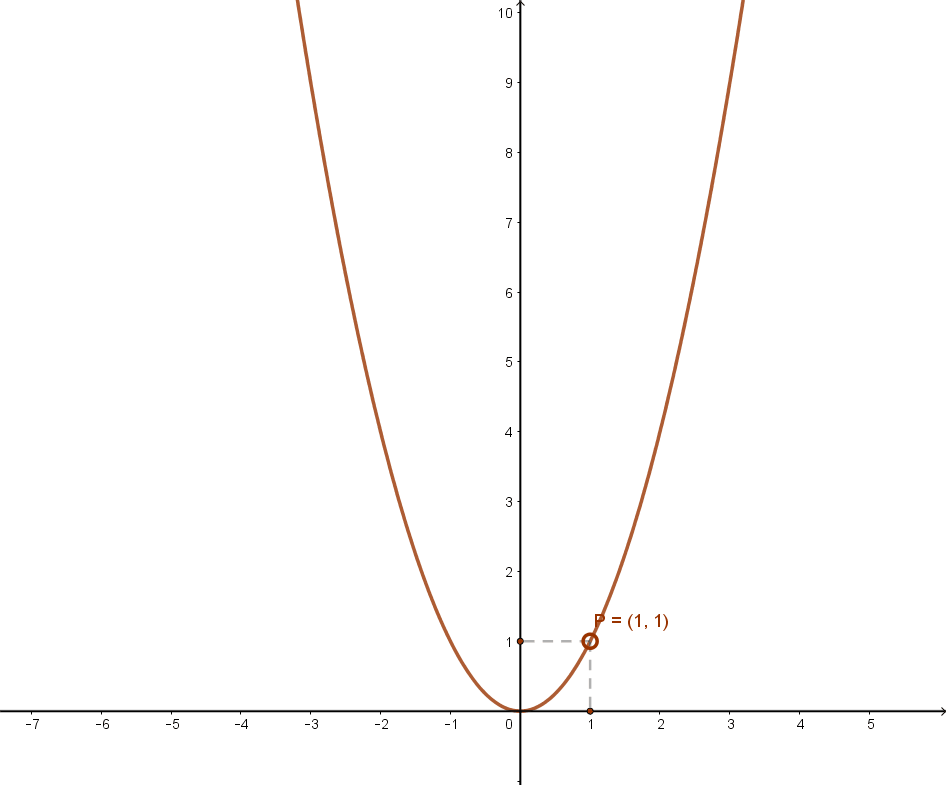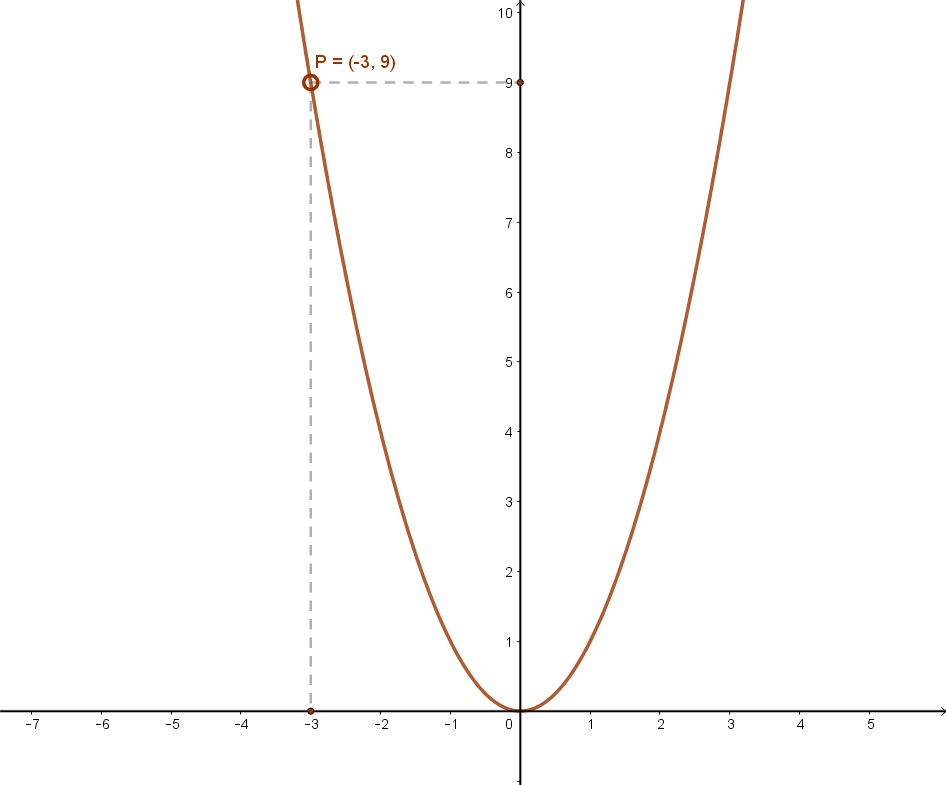
Az f:ℝ→ℝ, x→f(x) függvényt párosnak nevezzük, ha a H értelmezési tartomány minden x elemével együtt -x is a függvény értelmezési tartományához tartozik, és bármely x∈H-re f(-x)=f(x).
Azaz függvény az ellentett helyen ugyanazt a függvényértéket adja. Az ilyen függvények grafikonja szimmetrikus az „y” tengelyre.
Például:
Az m(x)=x2 másodfokú függvény alaphelyzetében páros függvény.
Definíció:
Az f:ℝ→ℝ, x→f(x) függvényt páratlannak nevezzük, ha az értelmezési tartomány minden x elemével együtt -x is a függvény értelmezési tartományához tartozik, és bármely x∈H-re f(-x)=-f(x).
Azaz függvény az ellentett helyen a függvényérték ellentettjét adja Az ilyen függvények grafikonja szimmetrikus az origóra.
Például:
A h(x)=x3 harmadfokú függvény alaphelyzetében páratlan függvény.
Periodikusság:
Definíció:
Az f:H→ℝ x→f(x) függvény periodikus (ismétlődő), ha van olyan p>0 állandó valós szám (ismétlési tényező), hogy az értelmezési tartomány minden x elemére f(x+p)=f(x).
Ha az ilyen p konstans számok között létezik legkisebb, akkor azt a p konstanst a függvény periódusának nevezzük.
A trigonometrikus függvények tipikusan periodikus függvények.
Példák:
s(x)= sin(x). Ennek a függvénynek a periódusa: p=2π.
Más példa:
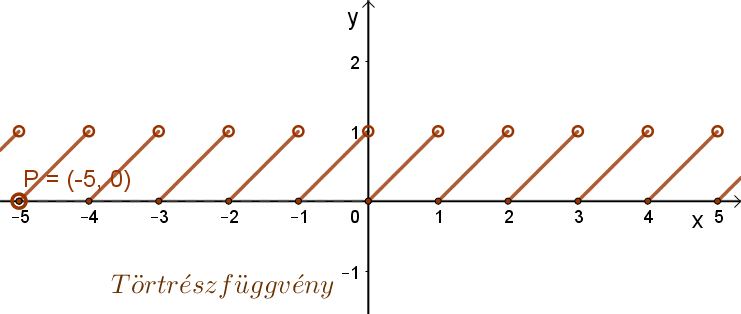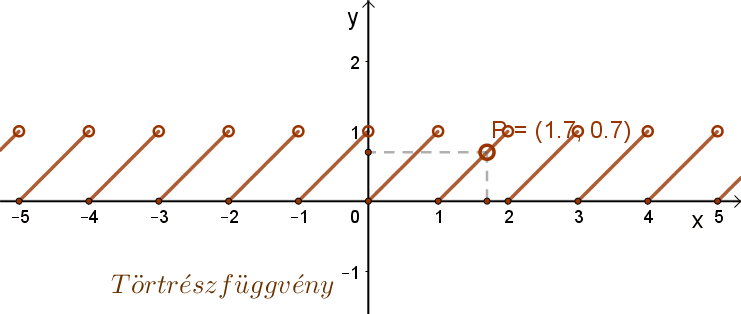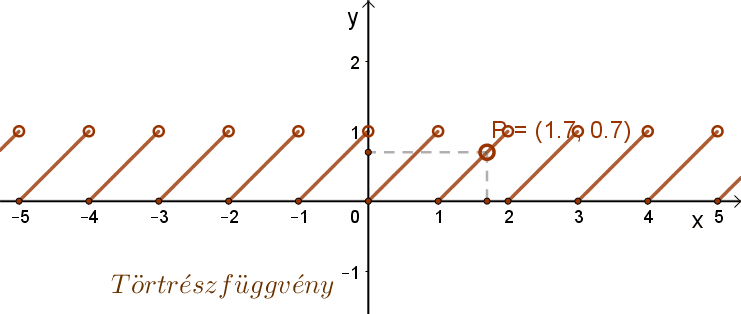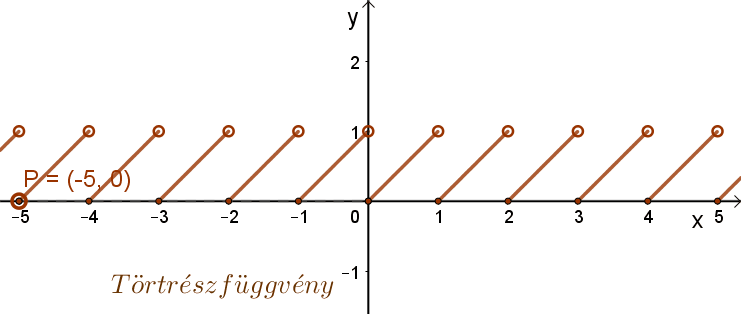
Periodikus függvény a törtrész függvény is. t(x)= {x}=x-[x]. Itt a periódus: p=1.
Konvexitás, konkávitás:
Definíció:
Az f:ℝ→ℝ, x→f(x) függvényt egy adott [a; b] intervallumon konvexnek mondjuk, ha minden a≤x1<x<x2≤b esetén \( f(x)≤\frac{f(x_{2})-f(x_{1})}{x_{2}-x_{1}}(x_{2}-x_{1}+f(x_{1}) \).
Azaz az intervallumon a függvénygörbe bármely két pontját összekötő húr a függvénygörbe fölött halad.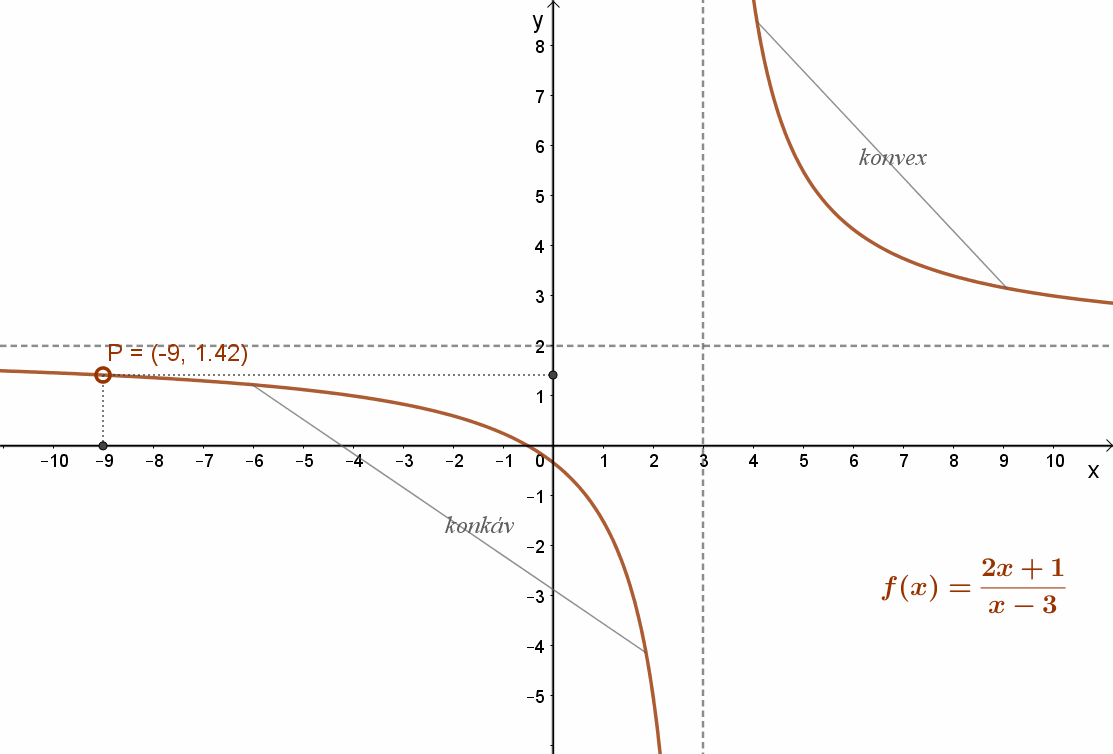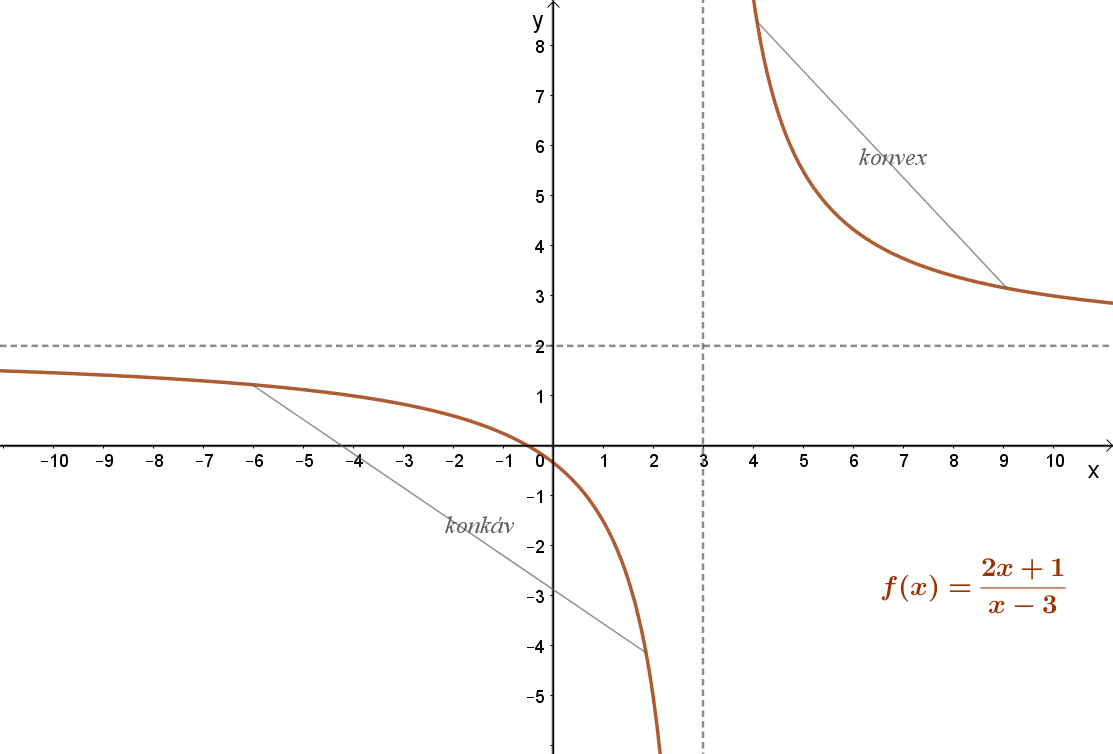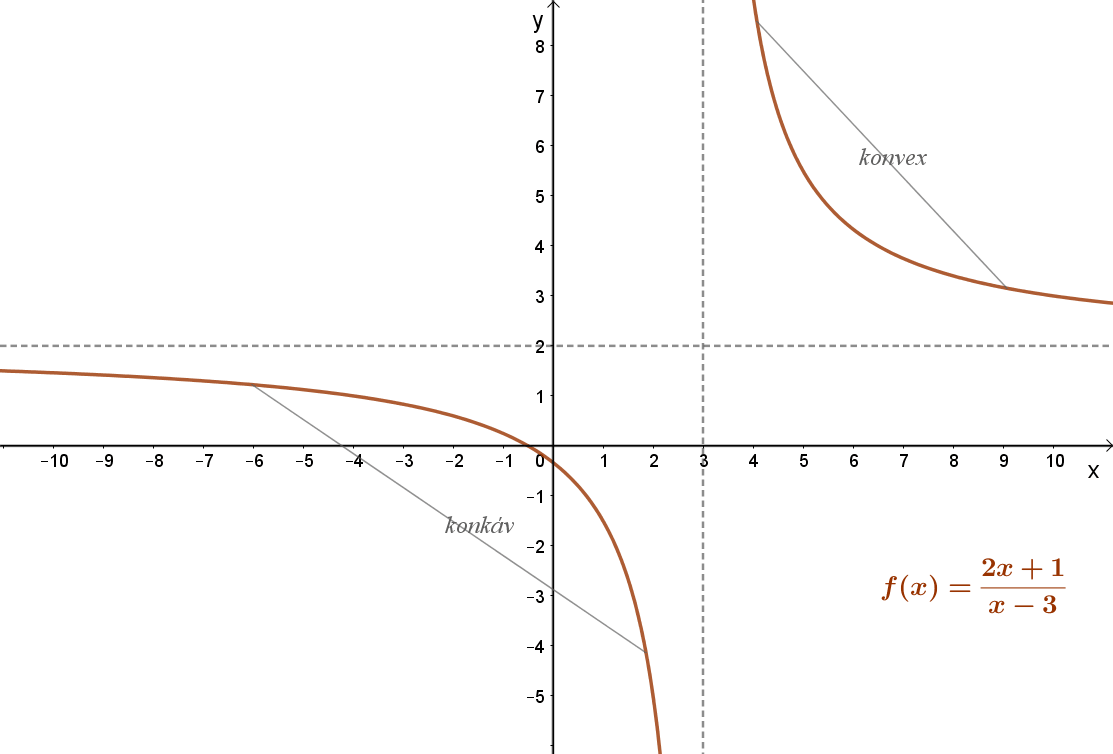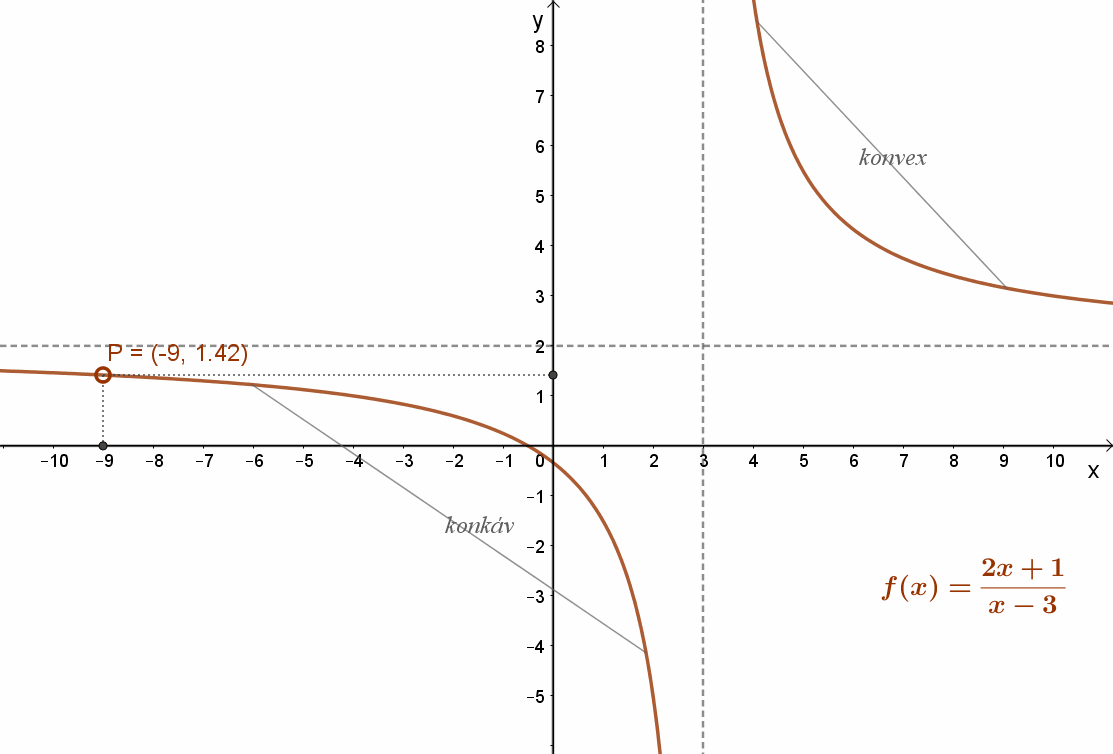
Konkáv függvény esetén a relációjel fordítva teljesül, azaz \( f(x)≥\frac{f(x_{2})-f(x_{1})}{x_{2}-x_{1}}(x_{2}-x_{1}+f(x_{1}) \).
Azaz konkáv függvény esetén az intervallumon a függvénygörbe bármely két pontját összekötő húr a függvénygörbe alatt halad.
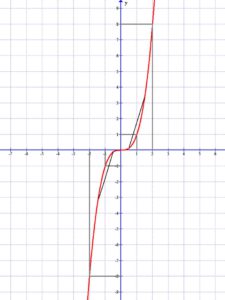
Például: Lásd a mellékelt függvényt: \( f(x)=\frac{7}{x-3}+2=\frac{2x+1}{x-3} \)
Inflexiós pont:
Definíció:
Az f(x) függvénynek x0∈Df pontban inflexiós pontja van, ha ebben a pontban a függvény konvexitása megváltozik. Konvexből konkáv vagy konkávból konvex lesz.
Lásd: f(x)=x3
Megjegyzés: Ha a függvénynek egy adott pontban inflexiós pontja van, akkor ott változik a konvexitás.
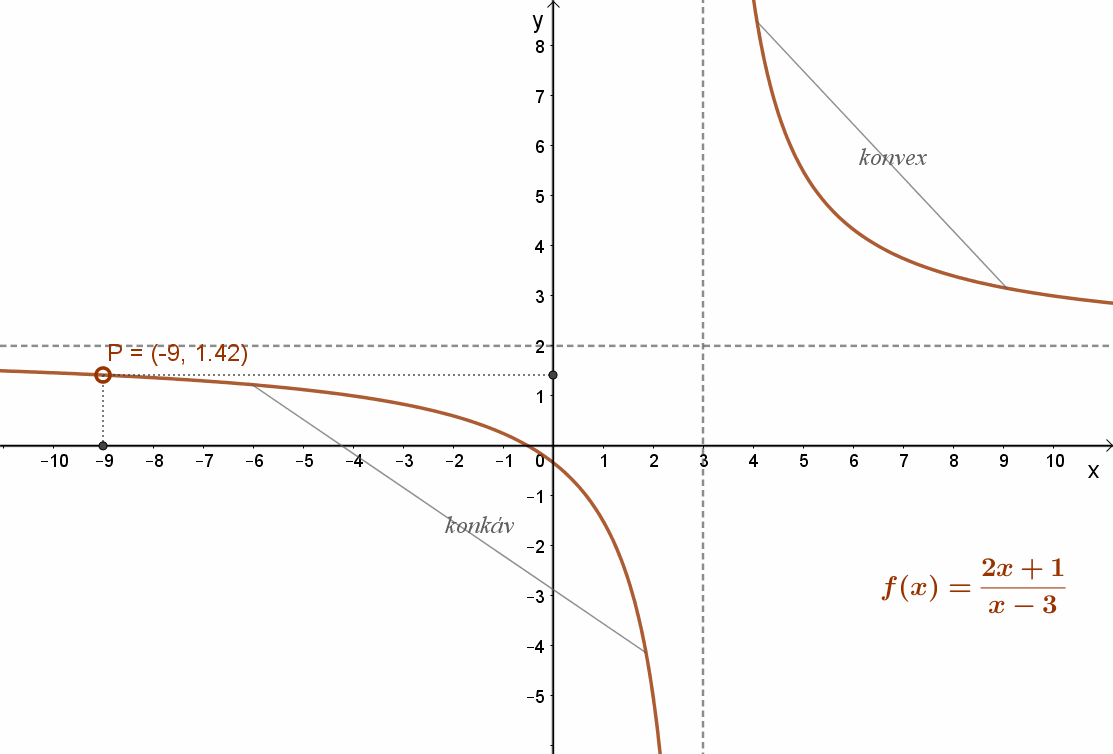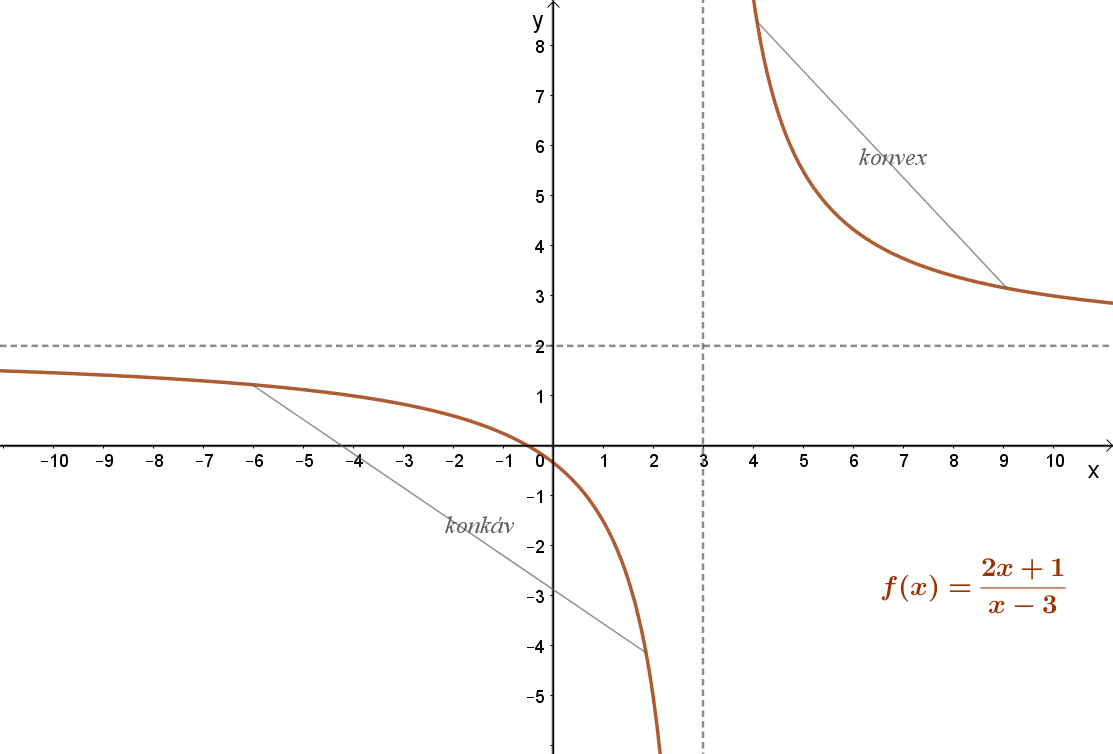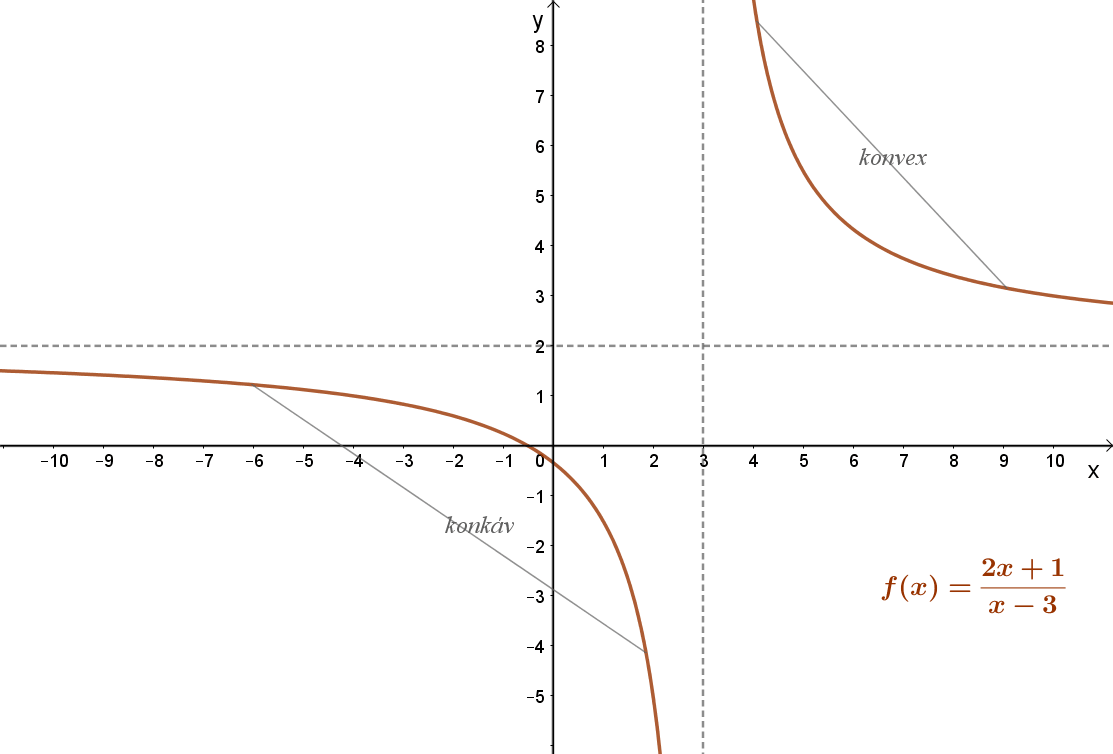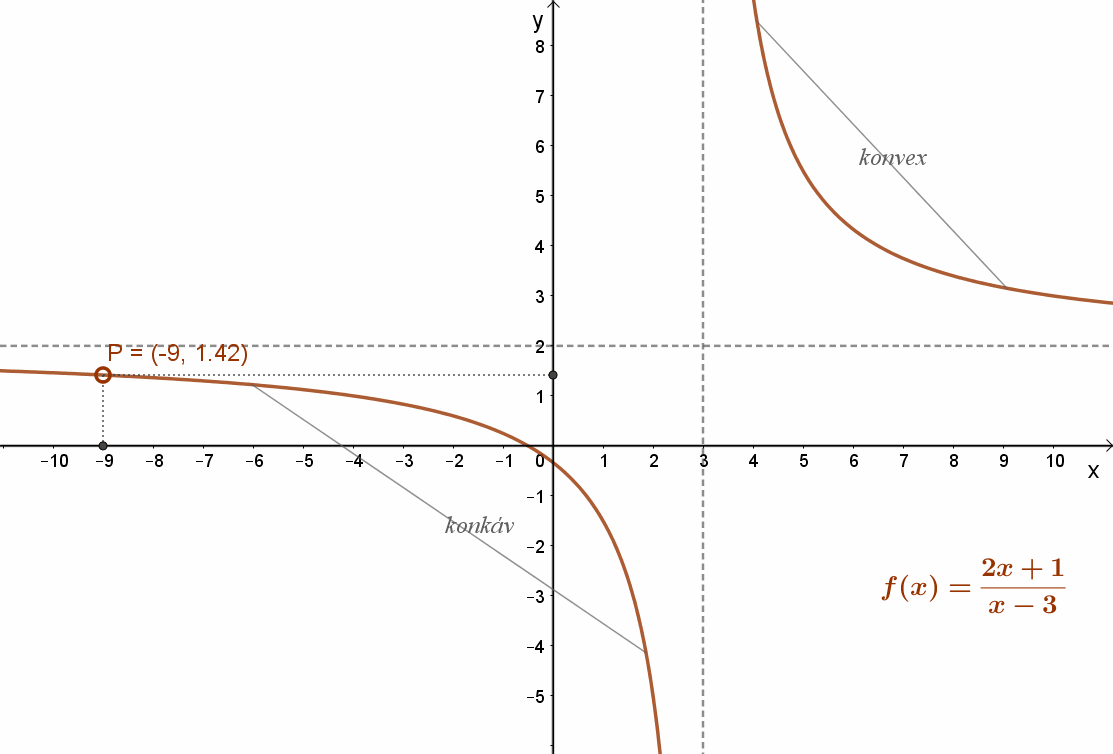Megfordítva nem igaz. Egy függvénynek megváltozhat a konvexitása, még sincs inflexiós pontja. Például ilyen a mellékelt : \( f(x)=\frac{7}{x-3}+2=\frac{2x+1}{x-3} \) függvény. Ez a függvény a ]-∞;3 intervallumon konkáv; a ]3;+∞]intervallumon pedig konvex. Inflexiós pontja viszont nincs, mert az x=3 helyen a függvény nem értelmezett.
Folytonosság:
Közép szinten a függvény folytonosságát nem definiáltuk, csak a függvény grafikonja alapján szemlétességnek megfelelően adjuk meg. Emelt szinten a definíció itt olvasható.
Például a h(x)=x3 harmadfokú függvény folytonos a valós számok halmazán.
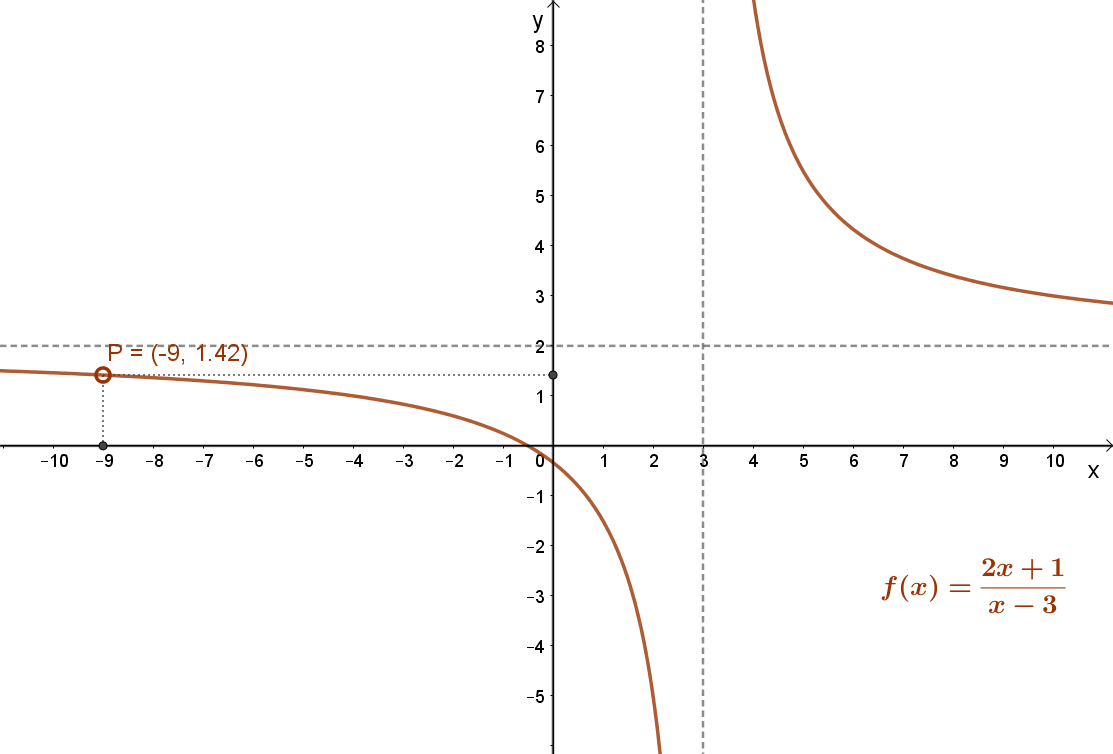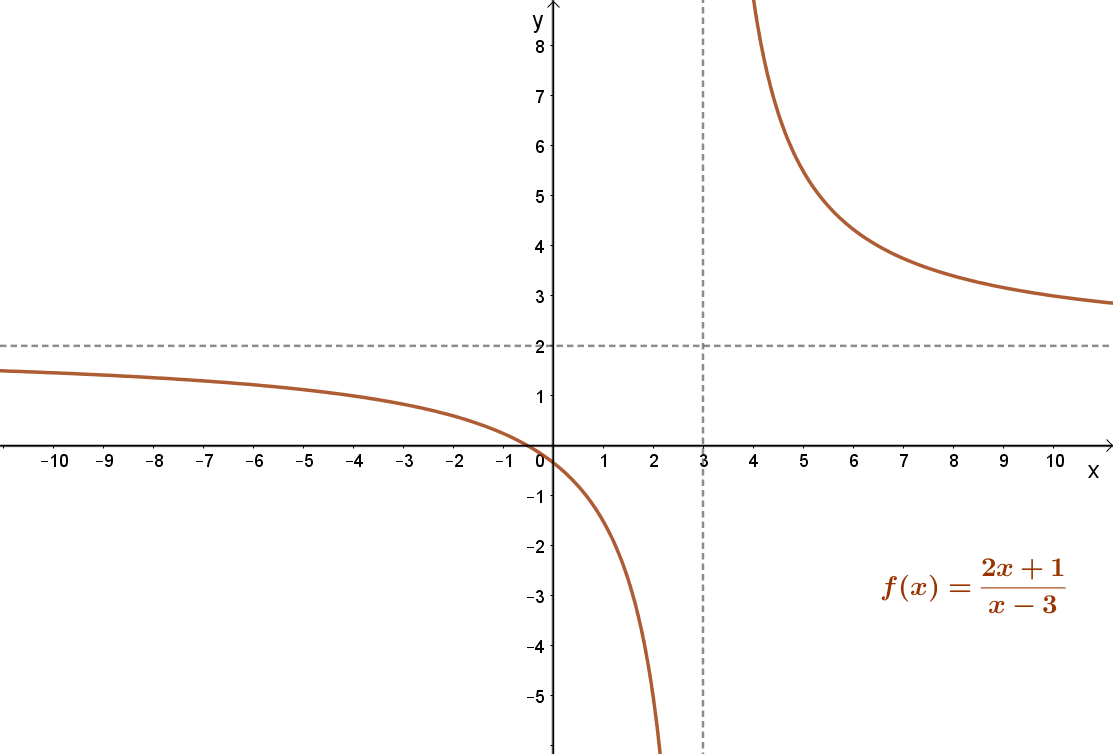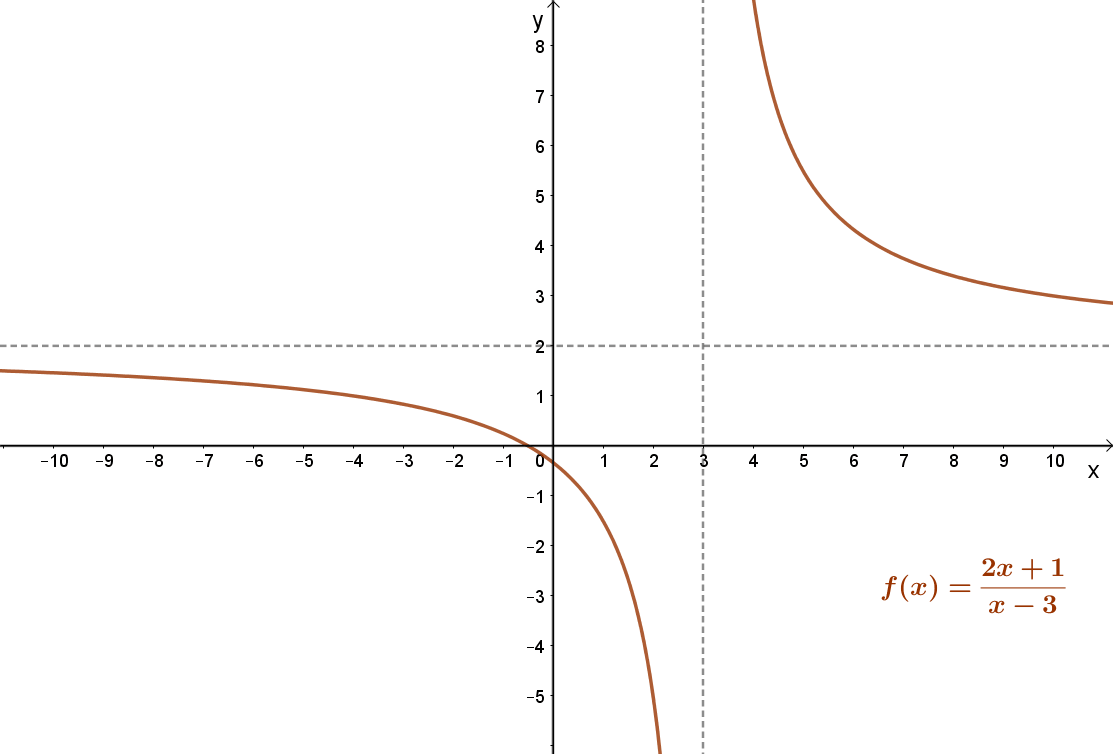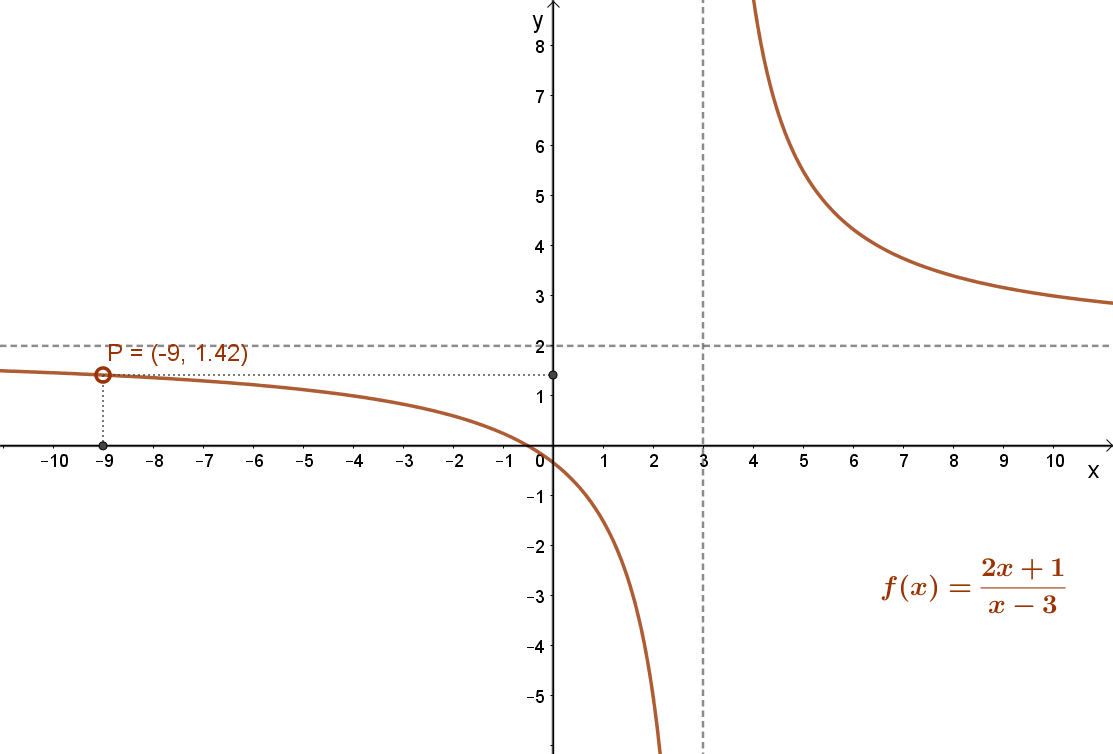
Ugyanakkor a \( f(x)=\frac{7}{x-3}+2=\frac{2x+1}{x-3} \) függvény nem folytonos az x=3 pontban.
Invertálhatóság:
Definíció:
Az f(x) függvénynek a g(x) függvény az inverze, ha az f(x) függvény értelmezési tartományának minden elemére teljesül, hogy az f(x) eleme a g(x) függvény értelmezési tartományának és f(g(x))=x.
Az f(x) függvény inverzét f–(x)-el jelöljük, azaz ha f(x) inverze a g(x) függvény, akkor f–(x)=g(x).
Egy függvény az alaphalmazának egy részhalmazán invertálható, ha ezen a részhalmazon értelmezhető a függvény inverze.
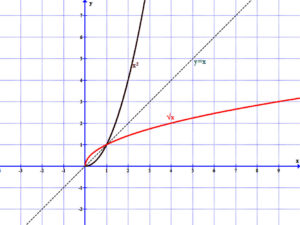Az f(x)=x2 függvény invertálható a nem-negatív számok halmazán és ezen az alaphalmazon inverze a négyzetgyök függvény.
\( f(x)=x^{2}, \; x≥0, \; f^{-}(x)=g(x)=\sqrt{x} \)
\( f(g(x))=(\sqrt{x})^2=x \)
És fordítva: \( g(f(x))=\sqrt{x^2}=x, \; ha \; x≥0 \).
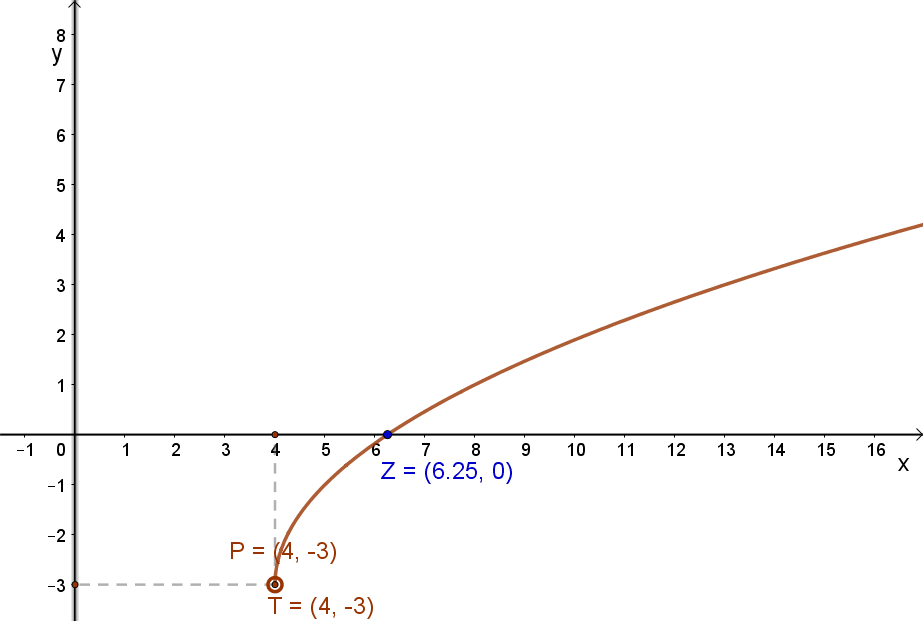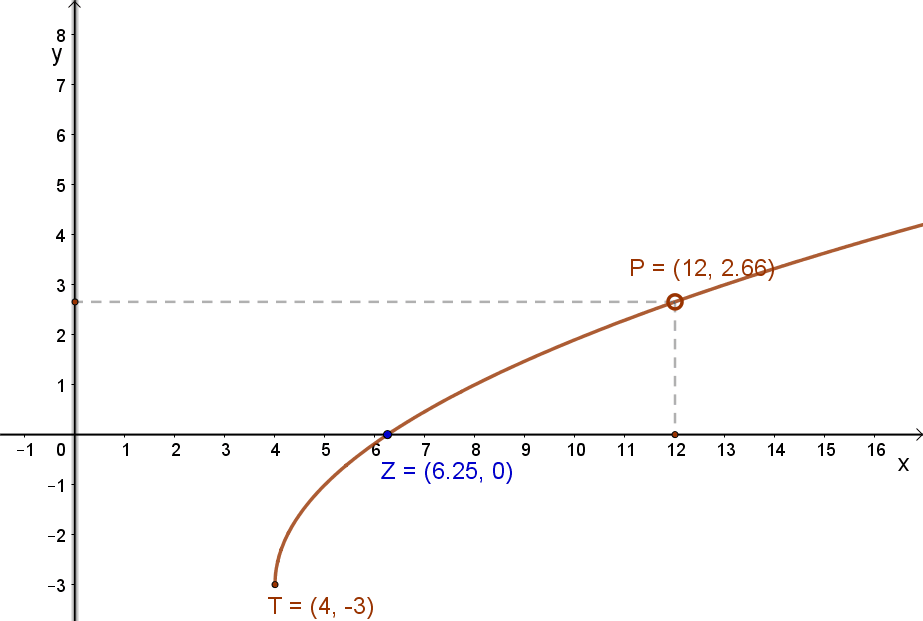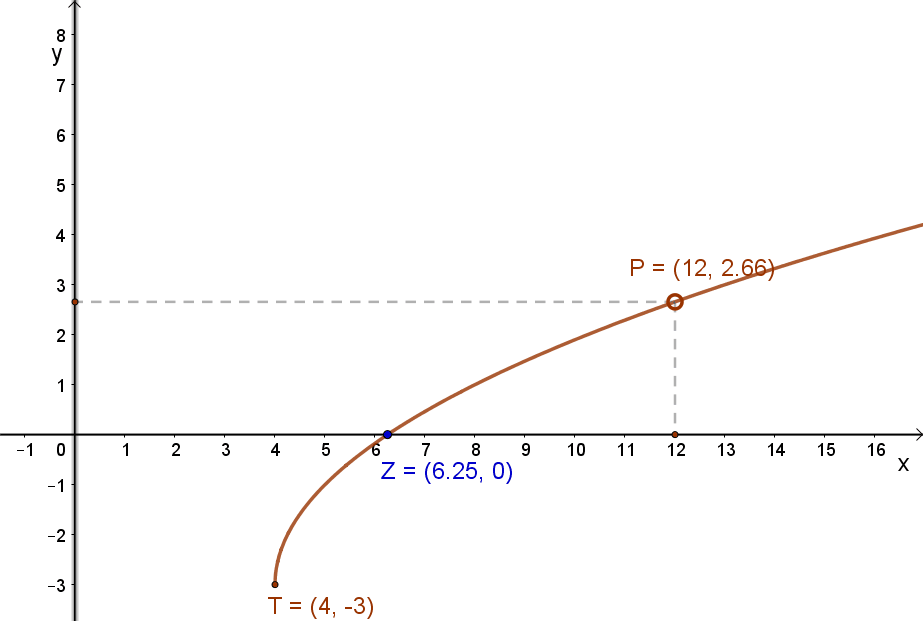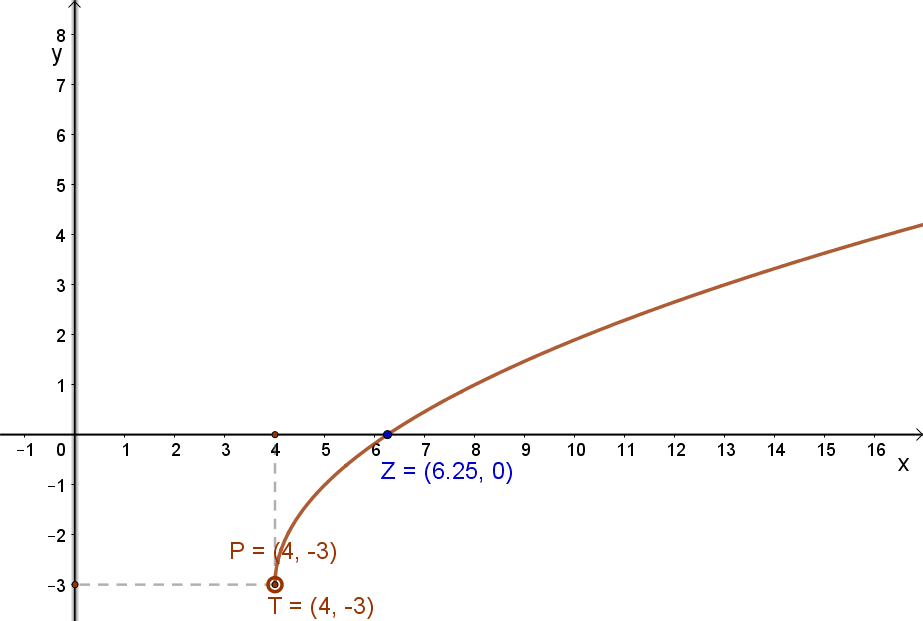
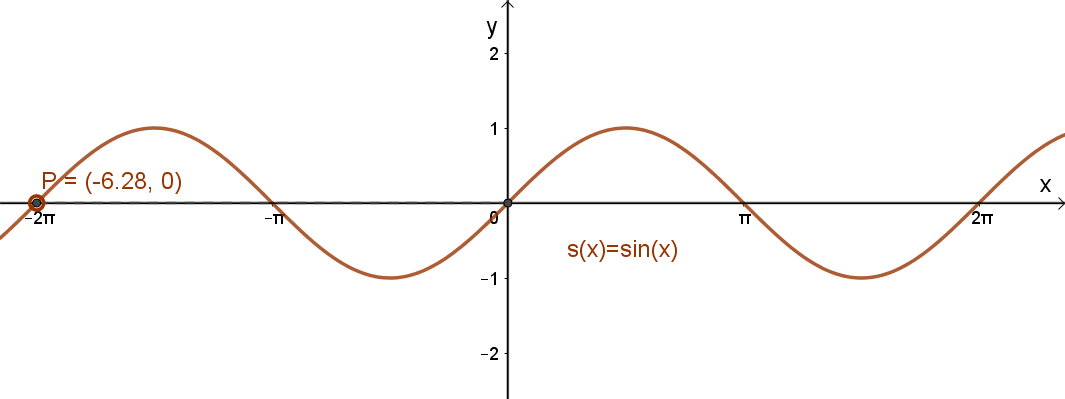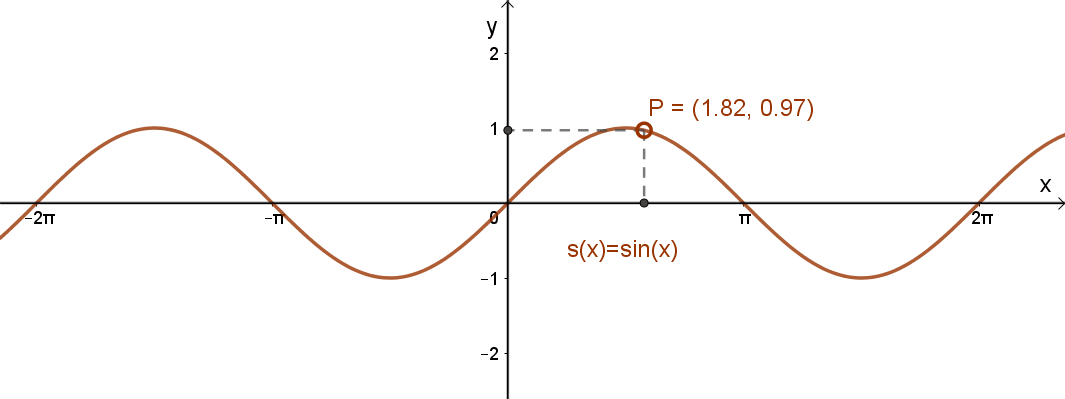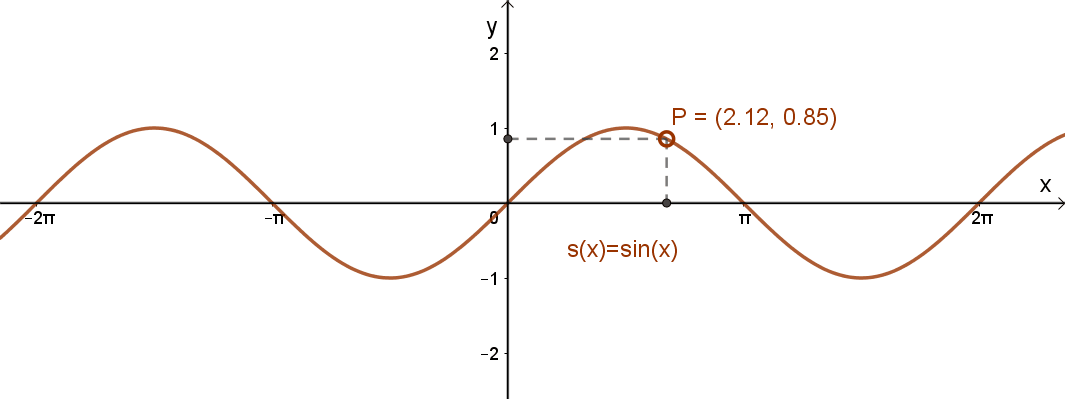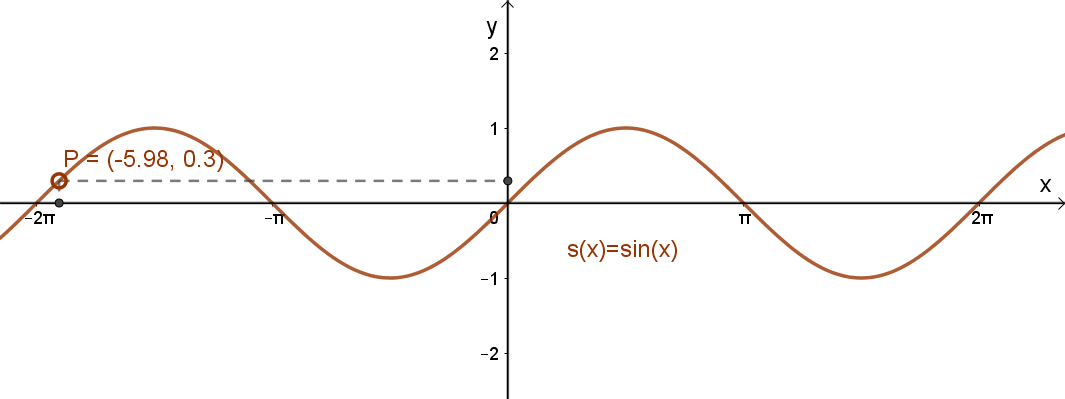
Comments are closed, but trackbacks and pingbacks are open.