Tetszőleges szög kotangensének definíciója: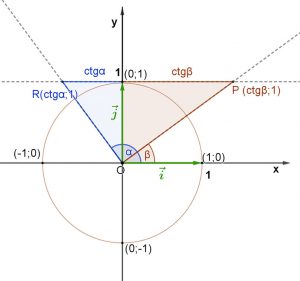
Tetszőleges szög kotangense a szög koszinuszának és szinuszának hányadosával egyenlő.
Formulával: \( ctgα=\frac{cosα}{sinα}, \; sinα≠0; \; α≠0+k· π , \; k∈ℤ \).
A definíciónak geometriai értelmezést is tudunk adni.
Egy szög kotangense, a koordinátasíkon annak a pontnak az x koordinátája, amelyet az adott szöggel elforgatott egységvektor egyenese az origó középpontú egységsugarú kör (0;1) pontjához húzott érintőből kimetsz.
Ha egy tetszőleges szöghöz hozzárendeljük a szög kotangensét, akkor a kotangens függvényt kapjuk.
Az x→ctg(x) függvény grafikonja:
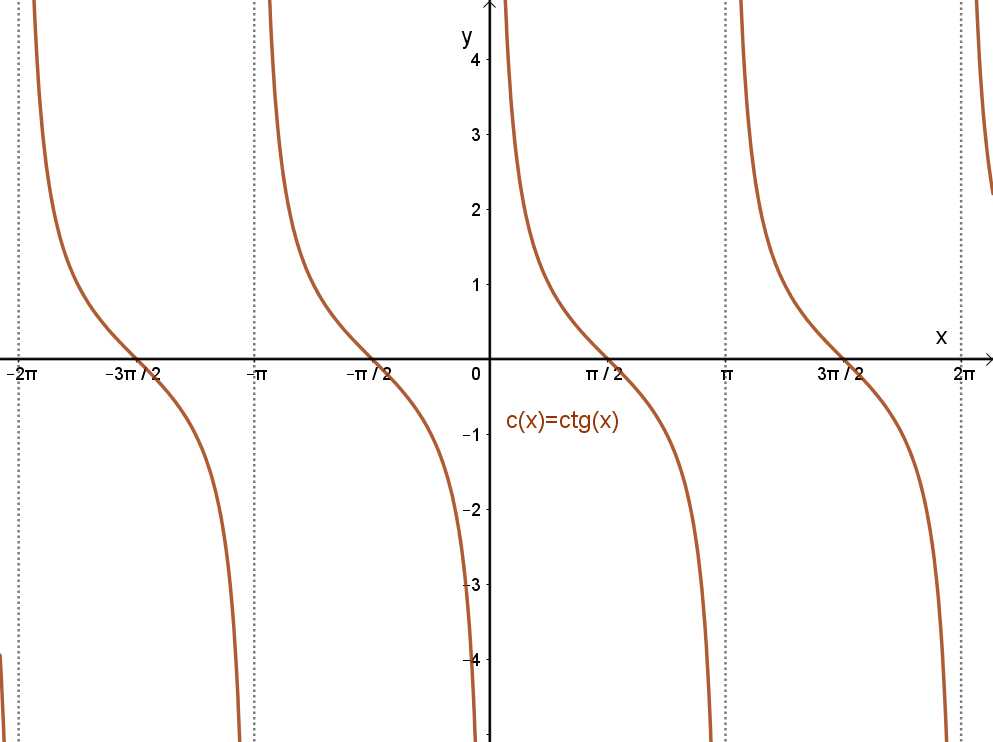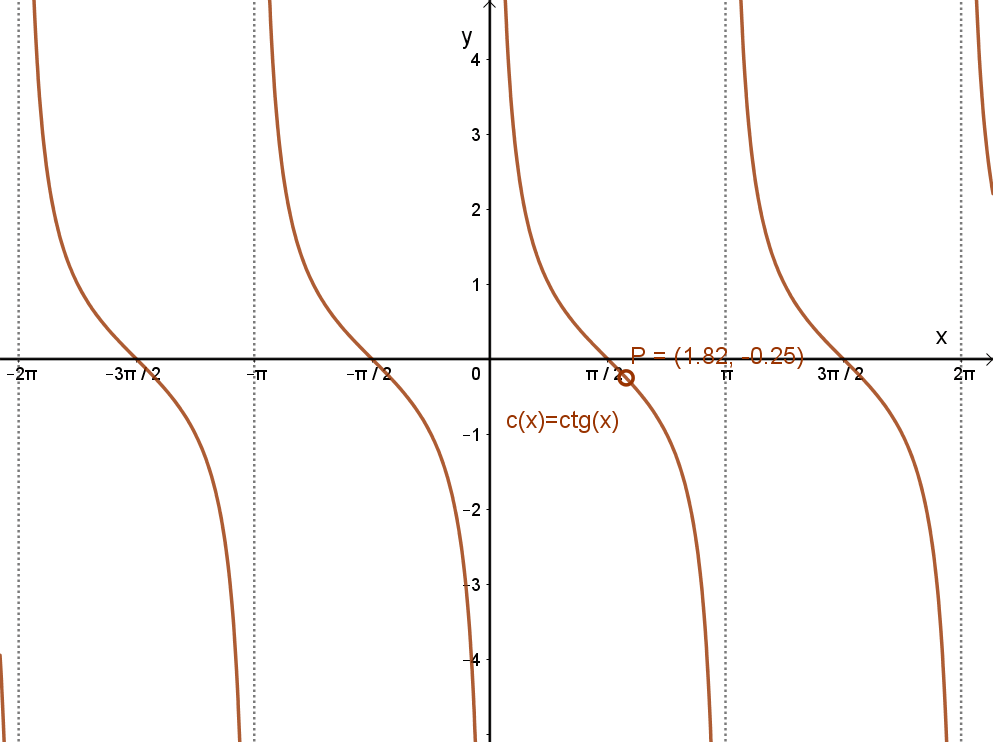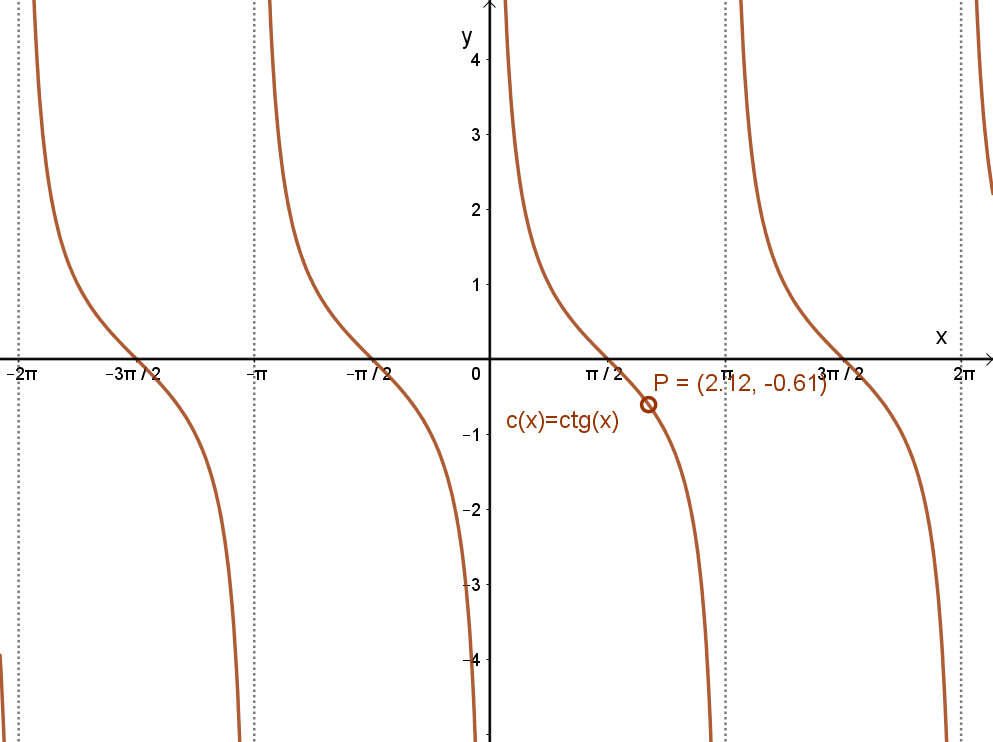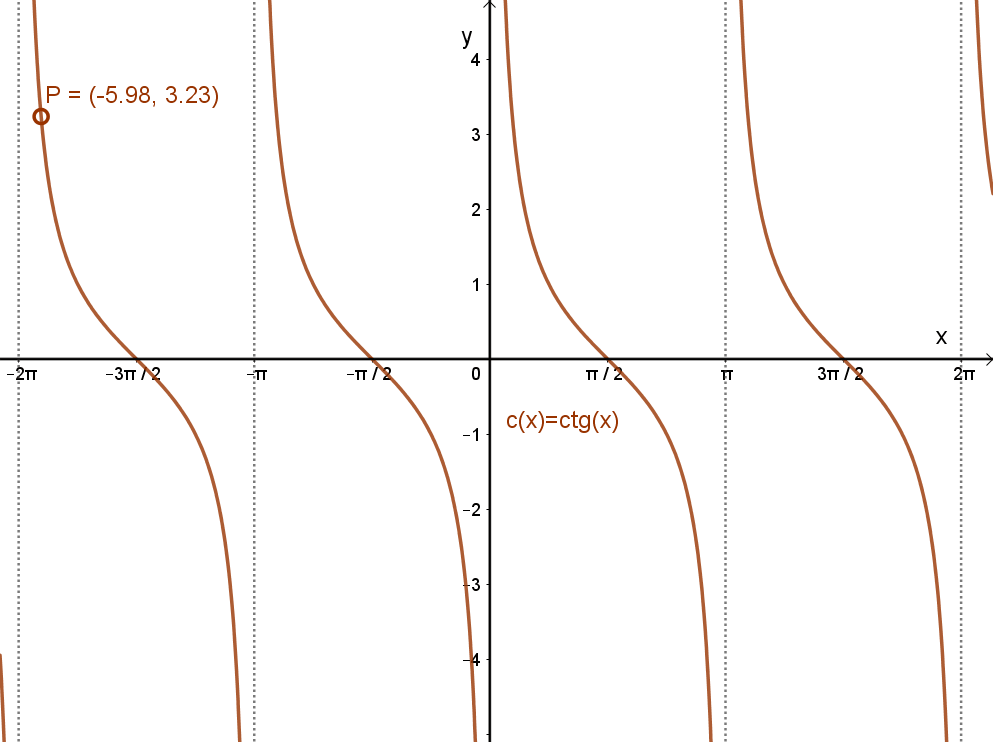
Az x→ctg(x) függvény jellemzése:
| Értelmezési tartomány: | x∈ℝ\{ 0+kπ; k∈ℤ}. |
| Értékkészlet: | y=ctg(x)∈ℝ. |
| Zérushelye: | x=π/2+kπ ; k∈ℤ. |
| Menete: | Minden (kπ, (k+1)π) intervallumon szigorúan monoton csökkenő. |
| Szélsőértéke: | Nincs. |
| Korlátos: | Nem. |
| Páros vagy páratlan: | Páratlan függvény. ctg(-x)=-ctg(x). |
| Periodikus: | Igen. A periódus hossza: p=π. |
| Konvex/konkáv: | Konvex, ha 0+kπ<x<π/2+kπ és konkáv, ha π/2+kπ<x<π+kπ, k∈ℤ |
| Folytonos: | Nem. x= 0+kπ; k∈ℤ helyeken szakadása van. |
| Inverz függvénye: | A (0;π) intervallumban invertálható. |
A kotangens függvény inverze az arkusz-kotangens függvény:
f-1(x)=arcctg(x):
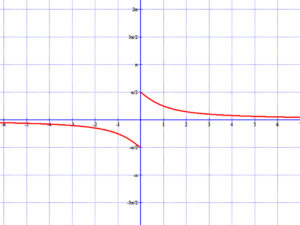


Comments are closed, but trackbacks and pingbacks are open.