A lineáris törtfüggvények általános alakja: \( f(x)=\frac{ax+b}{cx+d} \).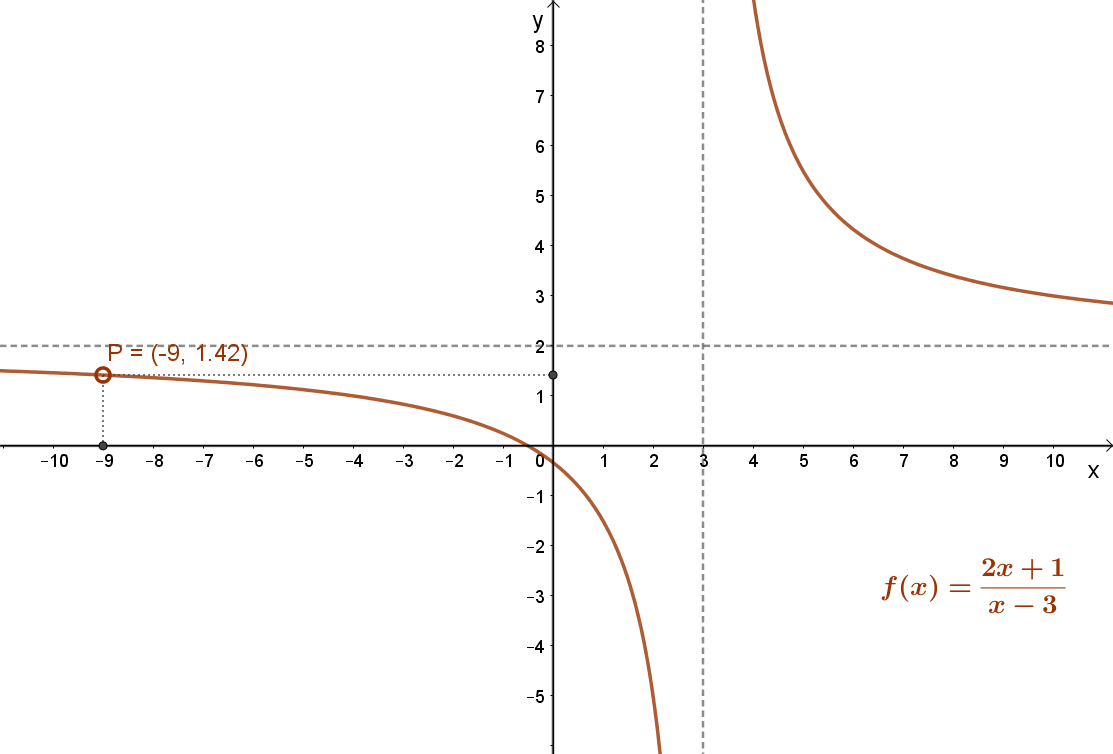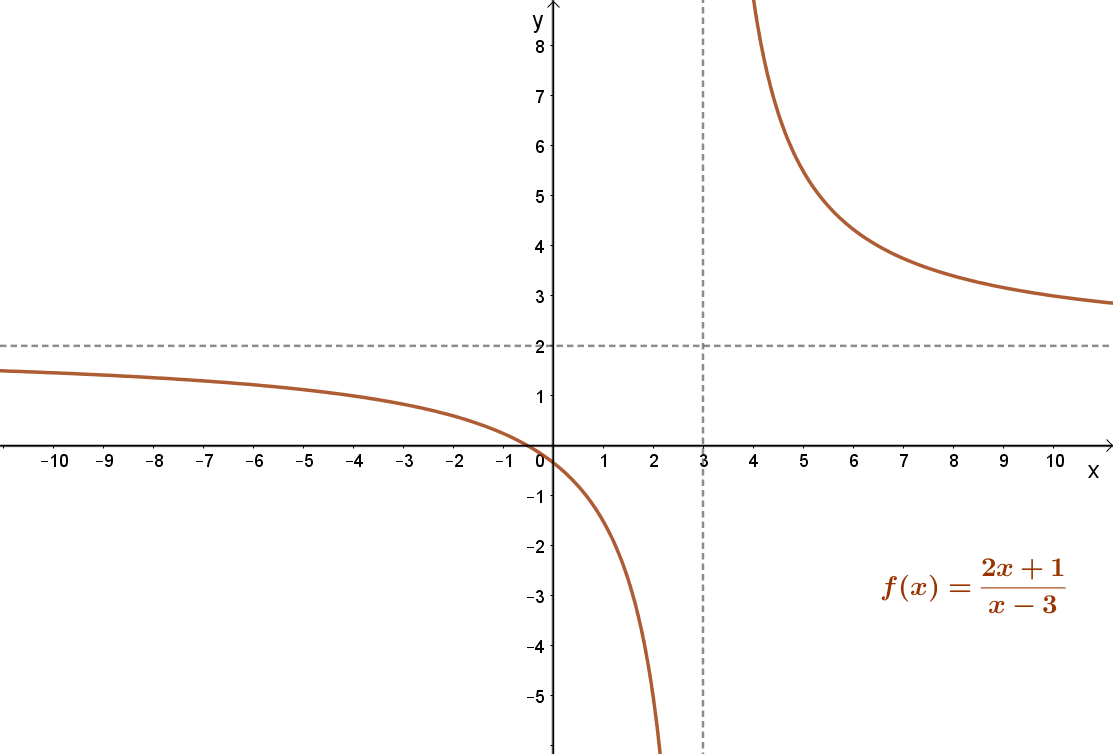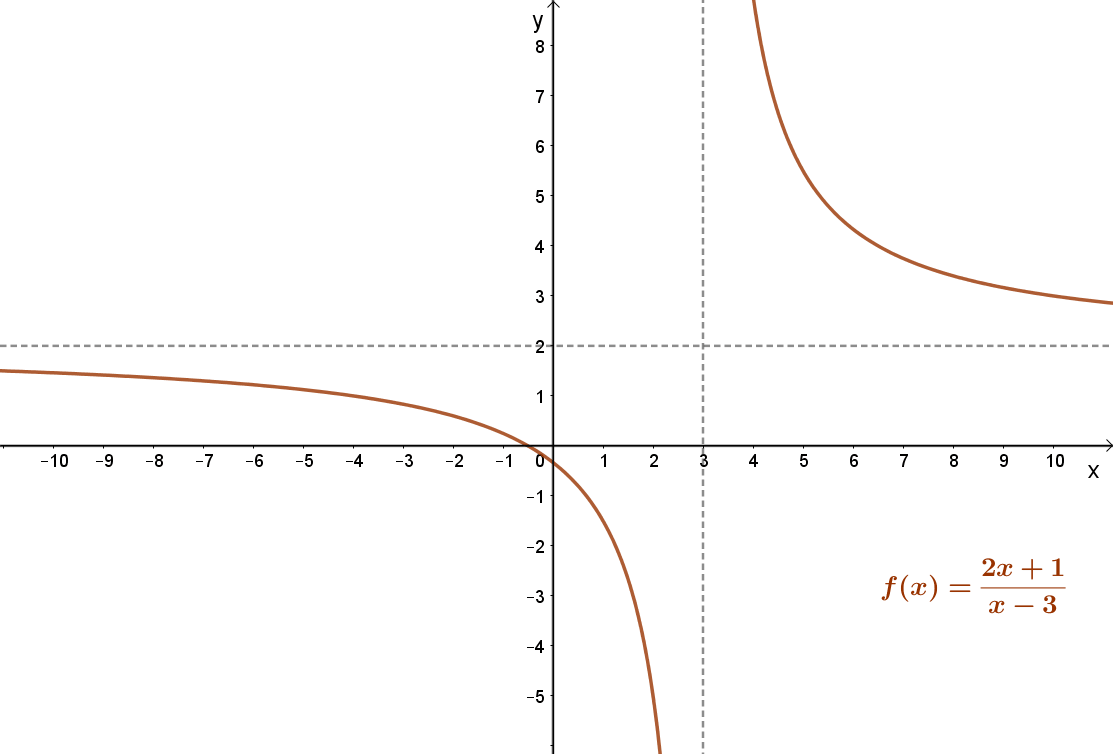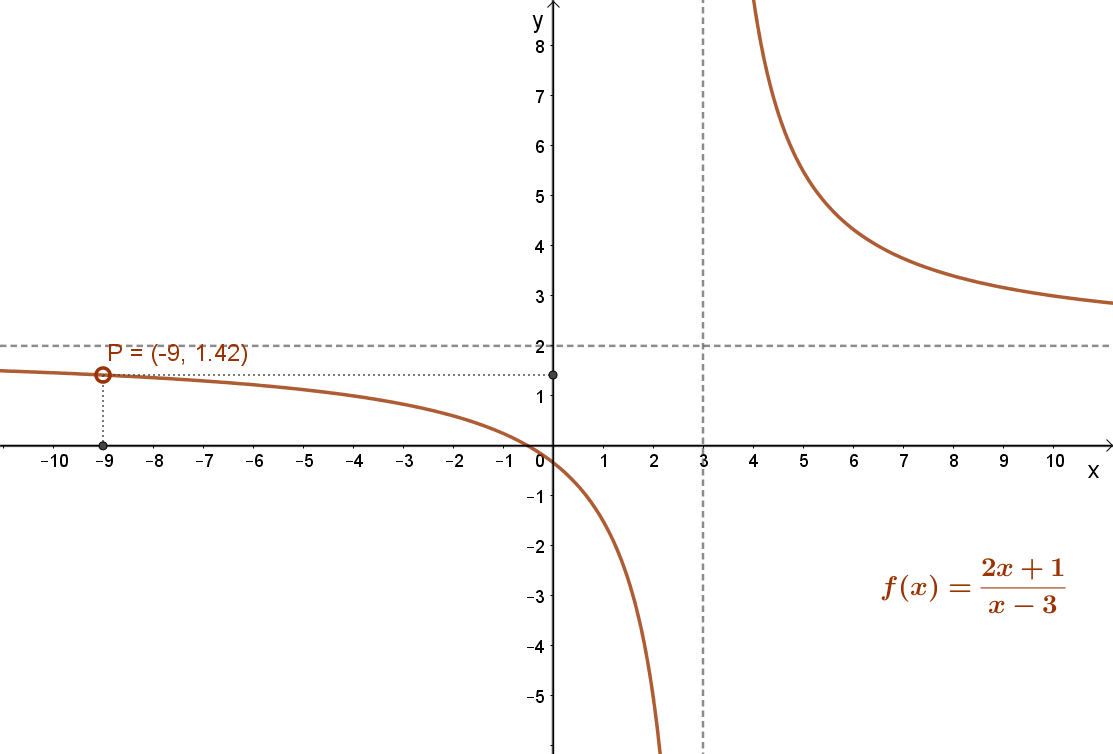 
Például: \( f(x)=\frac{2x+1}{x-3} \) .
Ez könnyen átalakítható a következő alakba: \( f(x)=\frac{7}{(x-3)}+2 \).
A függvény grafikonja egy hiperbola:
A \( f(x)=\frac{7}{(x-3)}+2 \) függvény jellemzése:
| Értelmezési tartomány: | x∈ℝ|x≠3. |
| Értékkészlet: | y=\( \frac{7}{(x-3)}+2 \)∈R|y≠2 |
| Zérushelye: | x=-0.5. |
| Menete: | Szigorúan monoton csökken, ha x<3 és szigorúan monoton csökken, ha nő, ha x>3. (3-hoz balról közeledve „tart” a -∞ felé, majd előbukkan a +∞-ben, és szigorúan monoton csökkenve tart a +2 felé.) |
| Szélsőértéke: | Nincs |
| Korlátos: | Nem. |
| Páros vagy páratlan: | Egyik sem. |
| Periodikus: | Nem. |
| Konvex/konkáv: | Konkáv, ha x<3 és konvex ha x>3. |
| Folytonos: | Nem. |
| Inverz függvénye: | Van. Ez pedig a \( f^{-}(x)=\frac{7}{x-2}+3 \) |
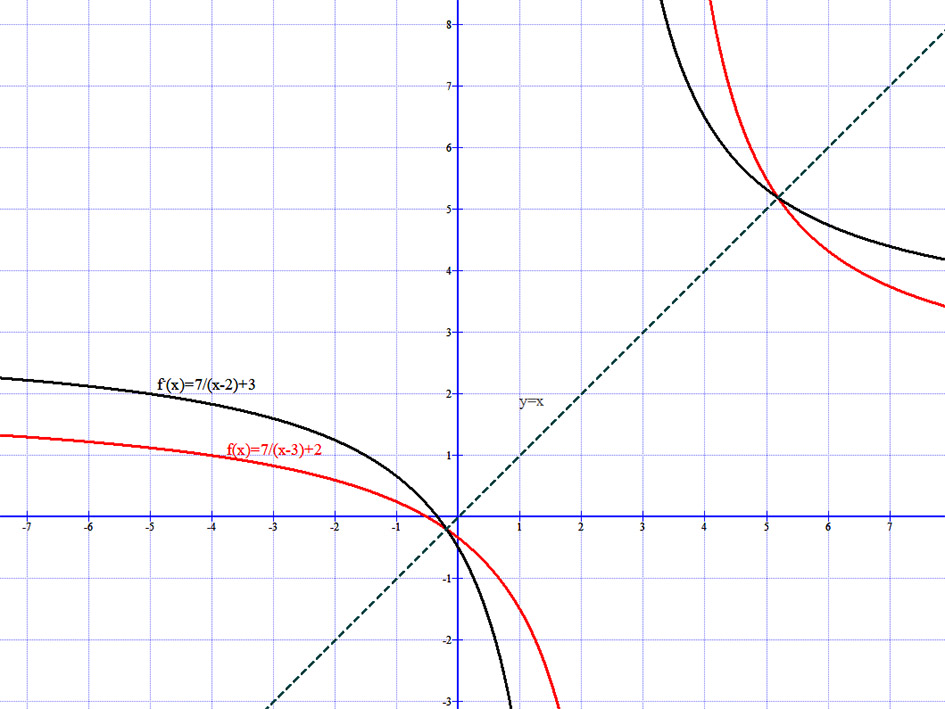
Az \( f(x)=\frac{7}{(x-3)}+2 \) és az inverzének, az \( f^{-}(x)=\frac{7}{x-2}+3 \) függvények grafikonja egy koordináta rendszerben:
A fo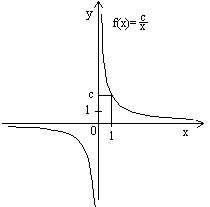
rdított arányosság függvénye \( f(x)=\frac{c}{x} \), amelyet reciprok függvénynek is neveznek, szintén lineáris törtfüggvény.
Ezek mindannyian a racionális törtfüggvények csoportjába tartoznak. A racionális törtfüggvények számlálója és nevezője egy valahányad fokú polinom.
A lineáris törtfüggvények esetében a számláló és a nevező egyaránt elsőfokú polinom.
Megjegyzés: az \( f(x)=\frac{ax+b}{cx+d} \) lineáris törtfüggvény ekvivalens átalakítása: \( f(x)=\frac{\frac{a}{c}(cx+d)+b-\frac{ad}{c}}{cx+d} \). Ez egyszerűbben \( f(x)=\frac{p}{cx+d}+q \) alakú.
Comments are closed, but trackbacks and pingbacks are open.