Definíció:
A pozitív valós számok halmazán értelmezett x→\( a^x \) típusú függvényt (a∈ℝ+; a>1 vagy 0<a<1) exponenciális függvénynek nevezzük.
Az exponenciális függvényt definiáló kifejezés egy olyan hatványkifejezésnek is tekinthető, amelyben a hatvány alapja konstans, a függvény változója a kitevőben szerepel és a függvény értéke hatvány értékével egyenlő.
A függvények grafikonja:
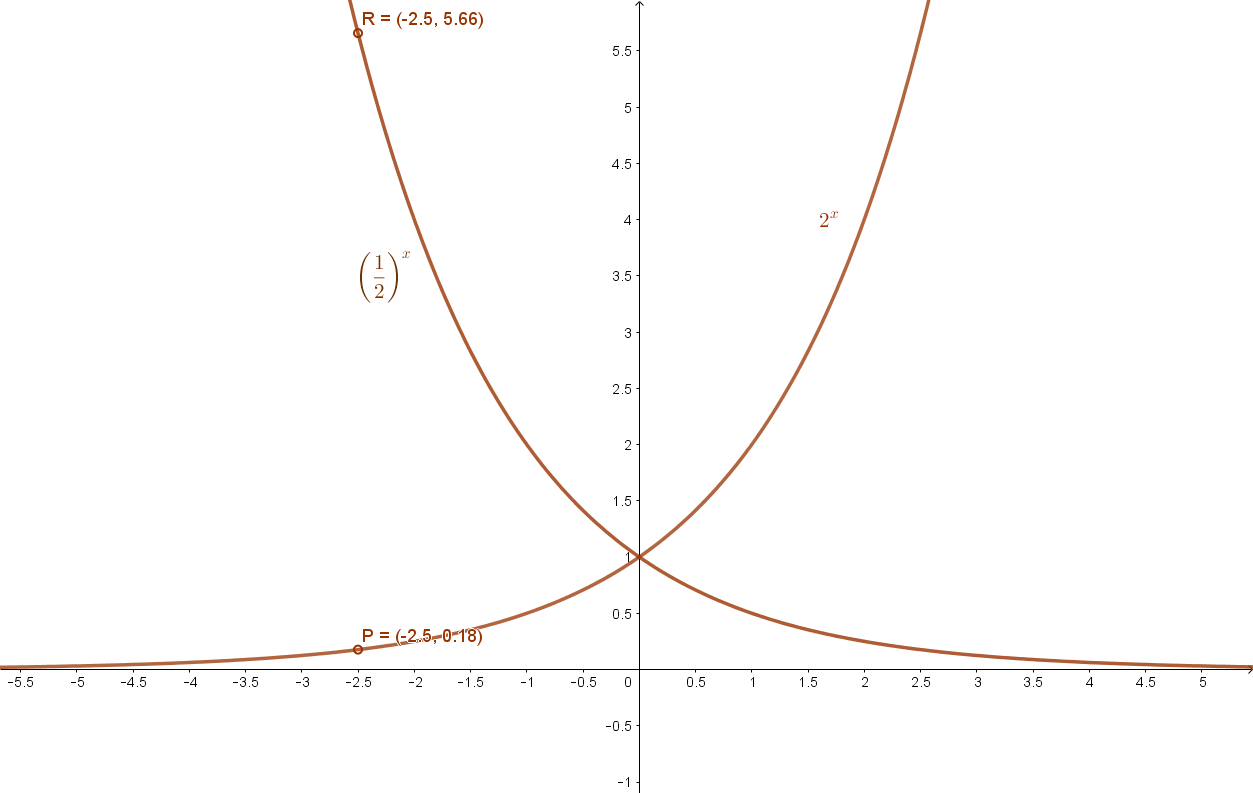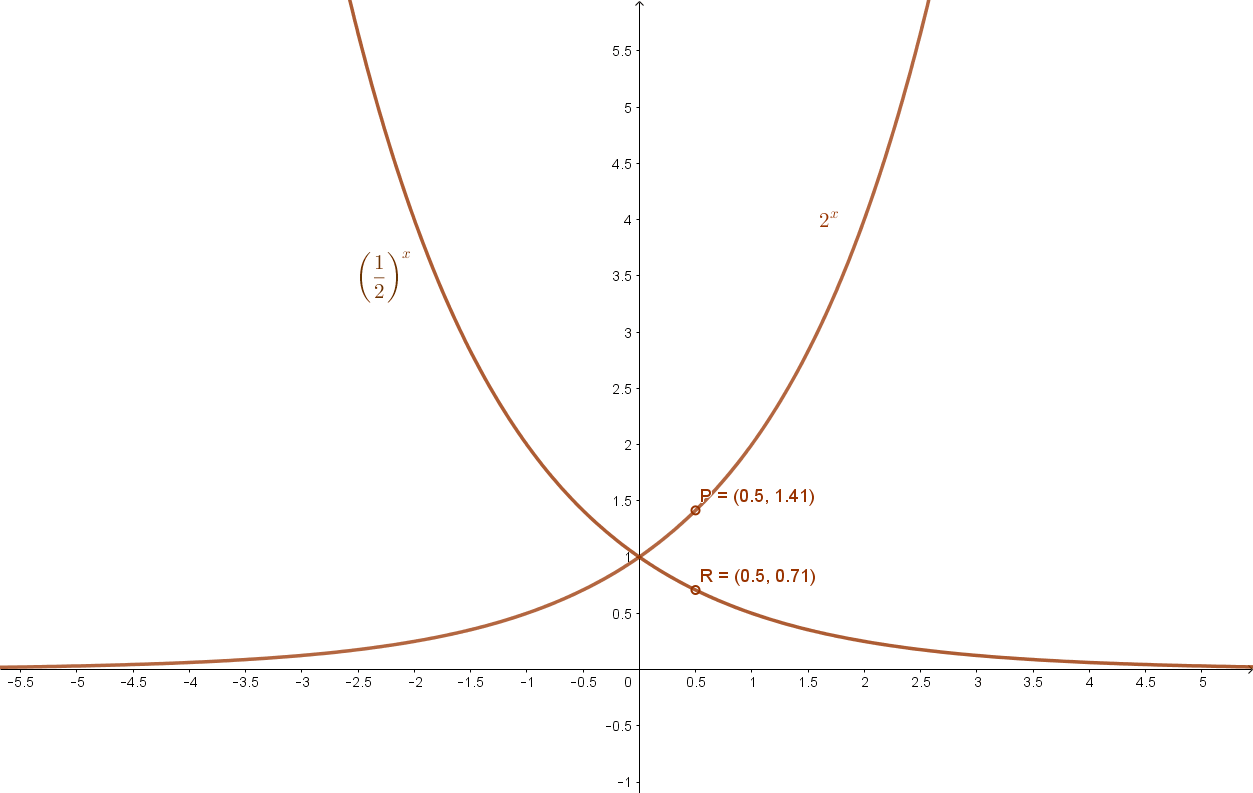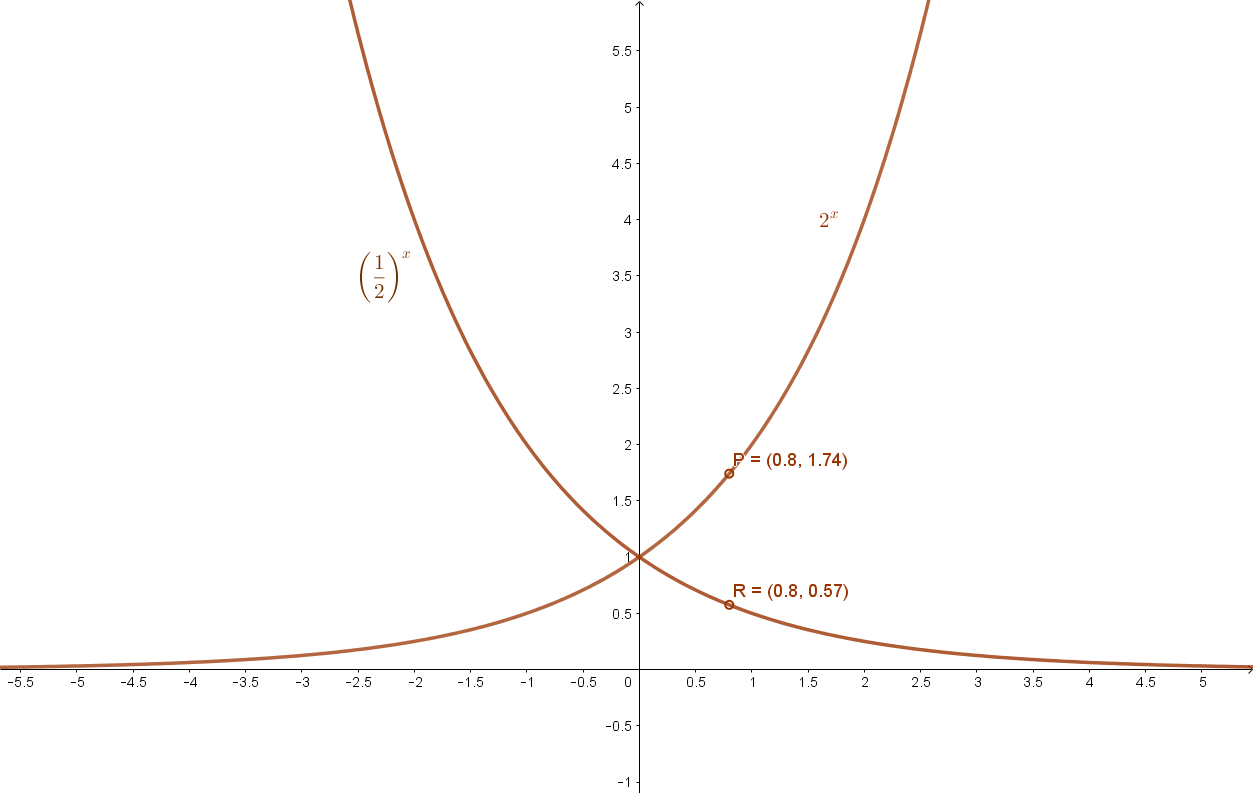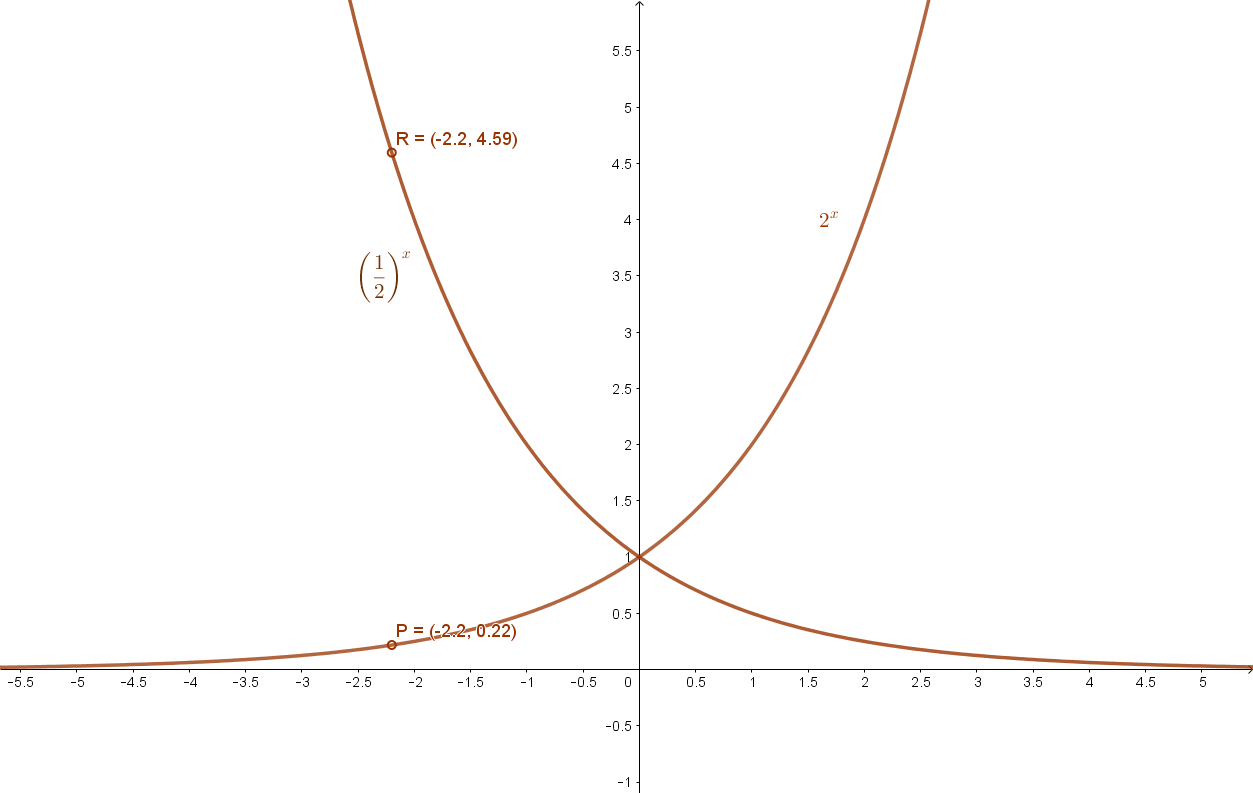
Az x→ax függvény jellemzése: (a>1, illetve 0<a<1 esetén)
| Értelmezési tartomány: | a∈ℝ. |
| Értékkészlet: | y=ax∈ℝ+. |
| Zérushelye: | Nincs. |
| Menete: | a>1 esetén szigorúan monoton nő; 0<a<1 esetén szigorúan monoton csökken. |
| Szélsőértéke: | Nincs. |
| Korlátos: | Nem. (Alulról igen.) |
| Páros vagy páratlan: | Egyik sem. |
| Periodikus: | Nem. |
| Konvex/konkáv: | Konvex. |
| Folytonos: | Igen. |
| Inverz függvénye: | A logaritmusfüggvény. |


Comments are closed, but trackbacks and pingbacks are open.