Mindjárt az elején felvetődik a kérdés: Mitől szabályos egy test?
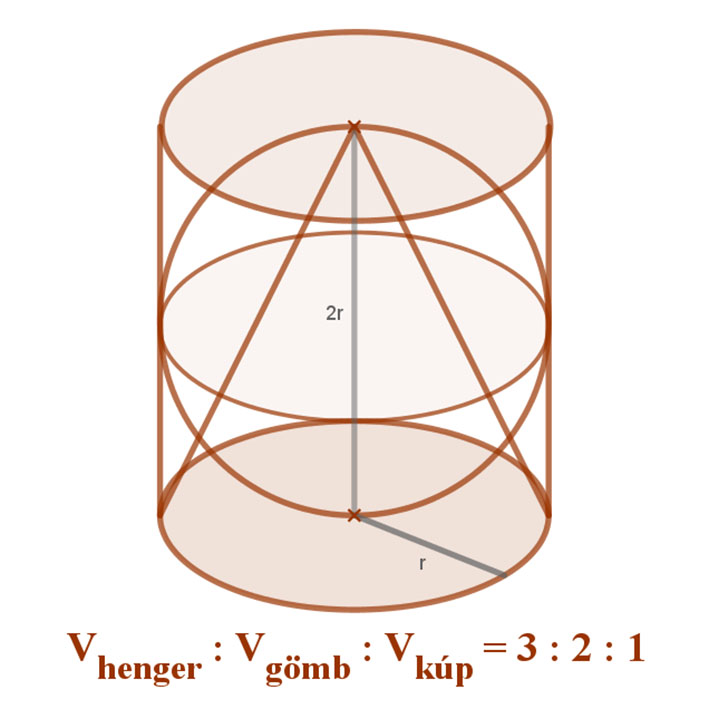 Az egyenes körhenger, az egyenes körkúp is rendelkezik szabályossággal.
Az egyenes körhenger, az egyenes körkúp is rendelkezik szabályossággal.
Talán még azt is mondhatnánk, hogy a legszabályosabb test a gömb.
Arkhimédész nem a szabályosságuk miatt kérte a síremlékére ezen testek rajzát, hanem az egymás írt testek térfogatainak az aránya ejtette ámulatba.
Akkor hát mit értünk szabályos testeken?
Definíció:
Szabályos testeknek nevezzük azokat a konvex poliédereket, amelyeknek élei, élszögei és lapszögei is egyenlők.
Megjegyzés:
Az olyan térrészt, amelyet véges sok sokszöglap határol, és amely teljes egyenest nem tartalmaz, poliédernek nevezzük.
„Kvázi” szabályos polidérek például az un. Archimédeszi testek.
Eukleidész „Elemek” című könyvében eljutott a szabályos testek ismertetéséig is. Bebizonyította, hogy csak 5 szabályos test (poliéder) létezik, több nem lehetséges.
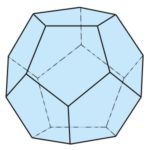
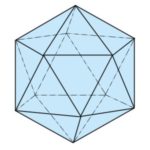
Az öt szabályos poliéder a következő:
|
|
|
|
|
|
|
A szabályos testek adatai:
| Lapok száma | Csúcsok száma | Élek száma | Oldallap éleinek száma | Egy csúcsba futó élek száma | |
| Szabályos tetraéder | 4 | 4 | 6 | 3 | 3 |
| Hexaéder (Kocka) | 6 | 8 | 12 | 4 | 3 |
| Oktaéder | 8 | 6 | 12 | 3 | 4 |
| Dodekaéder | 12 | 20 | 30 | 5 | 3 |
| Ikozaéder | 20 | 12 | 30 | 3 | 5 |
Leolvasható Euler tétele, amely a csúcsok, a lapok és az élek száma között mond ki összefüggést:
Lapok száma + csúcsok száma = élek száma + 2
A tételt már Descartes is ismerte, Euler azonban tőle függetlenül újra felfedezte.
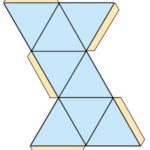
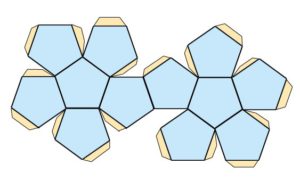
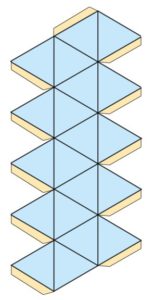
Az egyes testek elkészítése (hálója):
|
|
|
|
A szabályos testekkel már Pitagorasz és követői a püthagoreusok is foglalkoztak. Az ikozaédert már Babilonban is ismerték, és Pádua mellett találtak egy Kr.e. 500 előtti időből származó dodekaéder alakú etruszk emlékművet.
Az alábbiakban az arisztotelészi négy őselem (tűz, föld, levegő víz) és a szabályos testek kapcsolatát szemlélteti, ahogyan az ókori görögök képzelték:
|
|
|
|
|
|
|
Talán emiatt szokás a szabályos testeket platóni testek néven is emlegetni.

Feladat:
Egy a élhosszúságú kocka minden lapközéppontját kössük össze a szomszédos lapközéppontokkal, így egy szabályos oktaéder élhálózatát kapjuk! Mekkora az ehhez tartozó szabályos oktaéder felszíne és térfogata?
(Összefoglaló feladatgyűjtemény 2311. feladat.)
Megoldás:
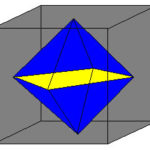
A mellékelt ábrán láthatjuk a kockát és benne a lapközéppontokat összekötő élekből kapott oktaédert.
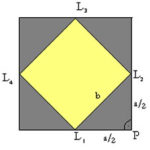 Ha a kockát felülnézetből nézzük, így látható az oktaéder síkmetszete. Az L1L2=b szakasz az oktaéder éle, amely az L1PL2 derékszögű háromszög átfogója. Ebből Pitagorasz tétele értelmében \( b=\sqrt{2}·\frac{a}{2} \)
Ha a kockát felülnézetből nézzük, így látható az oktaéder síkmetszete. Az L1L2=b szakasz az oktaéder éle, amely az L1PL2 derékszögű háromszög átfogója. Ebből Pitagorasz tétele értelmében \( b=\sqrt{2}·\frac{a}{2} \)
Felszín:
Mivel az oktaéder felszínét 8 db b oldalú egybevágó háromszög alkotja, ezért:
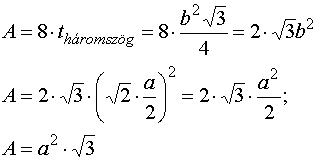
Térfogat:
Mivel az oktaéder térfogatát két darab olyan négyzet alapú gúla alkotja, amelynek alapéle és oldaléle is b, magassága pedig mindegyiknek a/2, ezért:
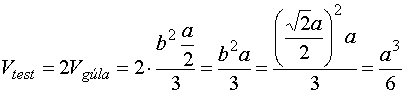


Comments are closed, but trackbacks and pingbacks are open.