Az egyenes körhenger térfogata

Az egyenes körhenger térfogatának meghatározásánál felhasználjuk, hogy a hasáb térfogata: V_hasáb=t_alapterület⋅m_hasáb.

Az egyenes henger térfogatát köré és beleírt hasábok segítségével, a kétoldali közelítés módszerével határozzuk meg.

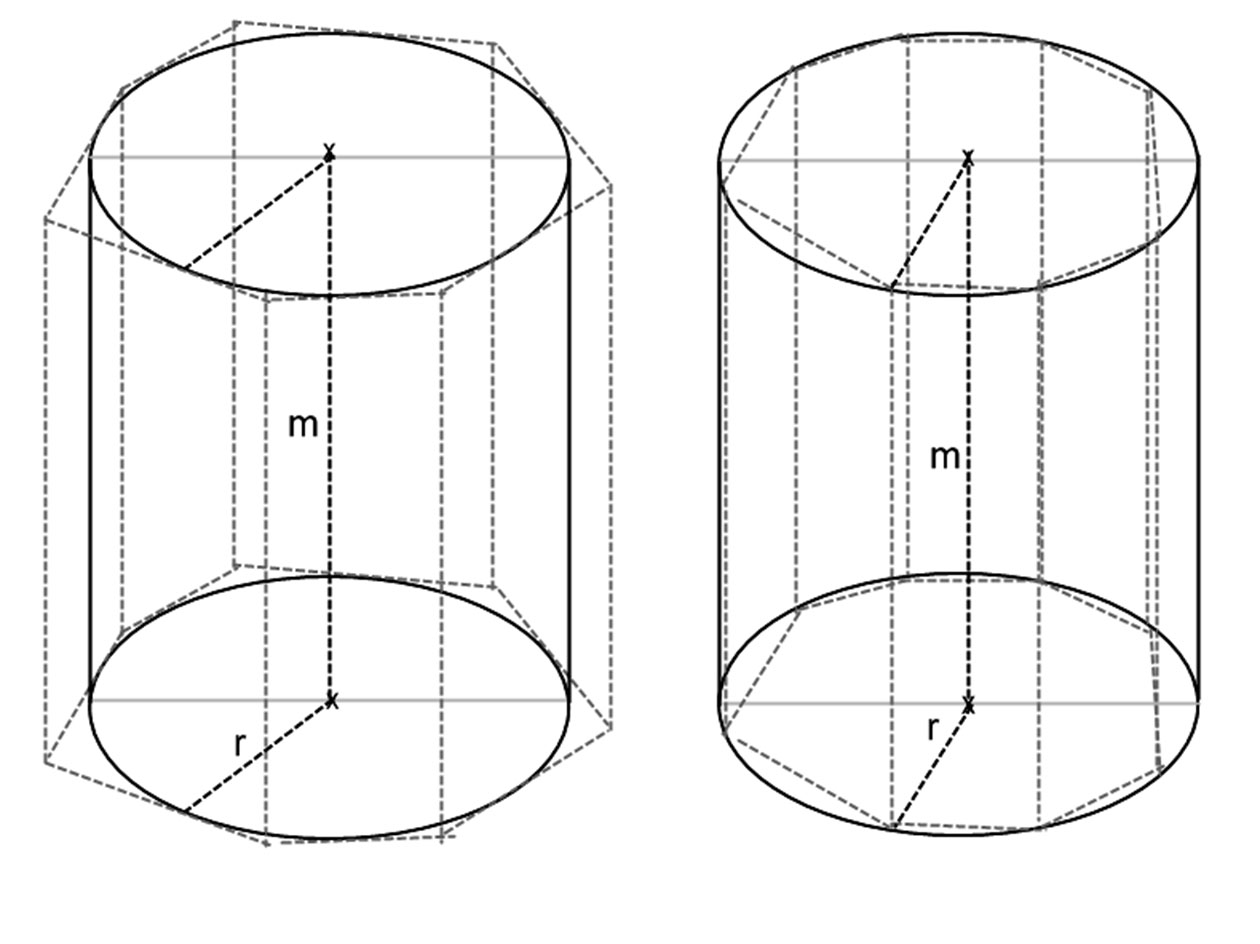A henger alaplapjába, azaz az r sugarú körbe és a kör köré egy-egy szabályos sokszöget írunk, melyek oldalszámai n=3, 4, 6, 8, stb. A beírt hasáboknál a sokszög csúcsai a körvonalon helyezkednek el, a köréírtaknál pedig a sokszögek oldalai (az alap és fedőlap alapélei) érintik a henger alap ill. fedőkörét. A hasábok és a henger alap és fedőlapjai egy síkba esnek. A beleírt hasábok térfogata mindig kisebb, a körírt hasábok térfogata pedig mindig nagyobb a henger térfogatánál, felírhatjuk tehát a következő egyenlőtlenségeket:

V_bele < V_henger <V_köré 

azaz:  V_bele =t_bele⋅m<V_henger<V_köré=t_köré⋅m.

Ahol m a henger és a hasábok magassága, t_bele és t_köréa bele és köré írt hasábok alaplapjainak területe.

A beleírt és köréírt hasábok oldalszámának növelésével a beleírt sokszög területe, így a beleírt hasáb térfogata is növekszik, míg a köréírt sokszög területe, vele együtt a hasáb térfogata csökken. A bele és a köréírt sokszögek oldalszámát növelve a két sokszög területe között a különbség bármilyen kicsivé tehető, és ez a kör területét, azaz r²π -t adja. Így tehát a henger térfogata: V_henger=t_kör⋅m_henger, azaz röviden: V=r²⋅π⋅m.

A henger, mint gabonatartály már a Kr. e 2000 körül feltűnik ókori egyiptomiaknál a Rhind papiruszon. Ez azt is megmutatja, hogy a henger térfogatát ki tudták számítani.

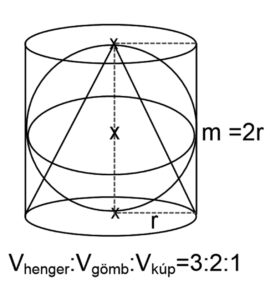Arkhimédész gyakorlatilag a fenti módszert (kimerítés módszerét) alkalmazta mind a henger, mind a gömb, mind a kúp térfogatának meghatározásánál. Egyik legszebb felfedezésének tartotta, hogy az egyenlő oldalú henger a beleírt gömb és kúp aránya: 3:2:1.