Gömb térfogata

Tétel:

A gömb térfogata: ​\( V_{gömb}=\frac{4·R^3· π }{3} \)​.

Ennek a bizonyításában is a Cavalieri-elvet fogjuk használni, mely szerint:

Ha egy síkon két olyan test van, amelyek

a. alapterülete egyenlő, és
b. az alaplapjukkal párhuzamos bármely síkkal képzett síkmetszetük páronként egyenlő területű,

akkor a két test térfogat egyenlő.

Vágjuk ketté a gömböt főköre mentén két egyenlő térfogatú részre. Nyilvánvalóan elegendő lesz egy félgömb térfogatát meghatározni.

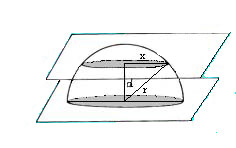A félgömböt a síkmetszetével, mint alaplappal ráhelyezzük egy síkra. A gömb sugara r. A Cavalieri-elv alapján az alapsíkkal párhuzamos síkmetszeteinek területét kell meghatározni. Az alapsíktól bármely d távolságban lévő síkmetszetének sugara x, területe: t=x²π=(r²-d²)π.

Ebben az összefüggésben a „d” a változó, azaz adott (fél)gömb esetén a metszet kör területe csak a „d” magasságtól függ.

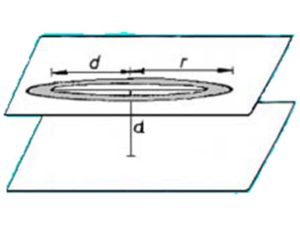Ha a fenti összefüggésben a zárójelet felbontjuk, akkor a t=r²π-d²π kifejezést
kapjuk. Ezt felfoghatjuk egy körgyűrű területének is.

A Cavalieri-elv alkalmazásához két dologra van szükségünk.

Egyrészt kell egy másik test, amelynek meg tudjuk határozni a térfogatát, valamint, hogy bármely síkmetszete megegyezik a félgömb síkmetszeteinek területével.

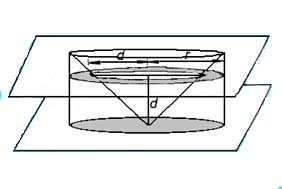A mellékelt ábrán látható egy a gömb „r” sugarával egyenlő sugarú és magasságú hengert. Vegyünk el ebből a képen látható módon egy egyenes körkúpot, amelynek alapkörének sugara és magassága is „r”. Ha ezt a maradék testet d magasságban elmetsszük, akkor a síkmetszet egy olyan körgyűrű lesz, amelynek külső köre állandó „r” sugarú.

Mivel a henger magassága egyenlő a gömb sugarával, ezért a kúp alkotója a henger alkotójával és sugarával egy egyenlőszárú derékszögű háromszöget határoz meg. Ebből következik, hogy a síkmetszet a kúpból a távolsággal egyenlő sugarú kört metsz ki, azaz a körgyűrű belső körének sugara a „d” változó. Ennek a körgyűrűnek a területe tehát: t=r²π-d²π.

A körgyűrű területe tehát minden „d” magasságban megegyezik a gömb ugyanezen magasságban történt síkmetszet területével. Ez azt jelenti, hogy a Cavalieri-elv szerint a félgömb térfogata megegyezik annak a testnek a térfogatával, amelyet akkor kaptunk, amikor a hengerből elvettük a kúpot.
Ennek a testnek a térfogata: ​\( V_{félgömb}=V_{henger}-V_{kúp}=r^2· π ·r-\frac{r^2· π ·r}{3}=\frac{2·r^3· π }{3} \)​.

A gömb térfogata ennek kétszerese, tehát:  ​\( V_{gömb}=\frac{4·R^3· π }{3} \)​.

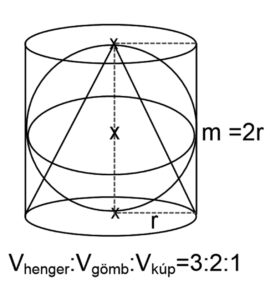Arkhimédész „A gömbről és hengerről” című munkájában meghatározta e testek felszínét és térfogatát. Azt, hogy a gömb felszíne egyenlő a köré írt henger palástjának területével. És a gömb térfogata a köré írt henger térfogatának 2/3-ad része, egyik legnagyobb felfedezésének tartotta. Ezért kérte, hogy halála után sírját egy hengerbe írt gömbbel jelöljék meg.

Feladat:

Három ólomgolyó sugara 5 cm, 8 cm és 12 cm. A három golyóból egyetlen golyót öntünk. Mekkora lesz ennek a sugara?

(Összefoglaló feladatgyűjtemény 2409. feladat.)

Megoldás:

Jelöljük a keresett új golyó sugarát r-rel. A három ólomgolyó térfogata:
​\( V_{1}=\frac{4·5^3· π }{3} \)​ , ​\( V_{2}=\frac{4·8^3· π }{3} \)​, ​\( V_{3}=\frac{4·12^3· π }{3} \)​.

Az öntés után kapott golyó térfogata ennek a három térfogatnak az összege, azaz: ​\( V_{új}=V_{1}+V_{2}+V_{3}=\frac{4·5^3· π }{3}+\frac{4·8^3· π }{3}+\frac{4·12^3· π }{3} \)​ .

Ennek kell megegyeznie a ​\( \frac{4·r^3· π }{3} \)​ -mal.

Így tehát a következő összefüggést kapjuk: ​\( \frac{4·R^3· π }{3}=\frac{4·(5^3+8^3+12^3)· π }{3} \)​ .

Az egyszerűsítések után: r³=5³+8³+12³=125+512+1728=2365.

A köbgyökvonás elvégzésével r ≈13,32 cm adódik.