Ptolemaiosz görög matematikusról elnevezett tétel a húrnégyszögekhez kapcsolódik és a húrnégyszögek oldalai és átlói között fogalmaz meg egy összefüggést.
Tétel:
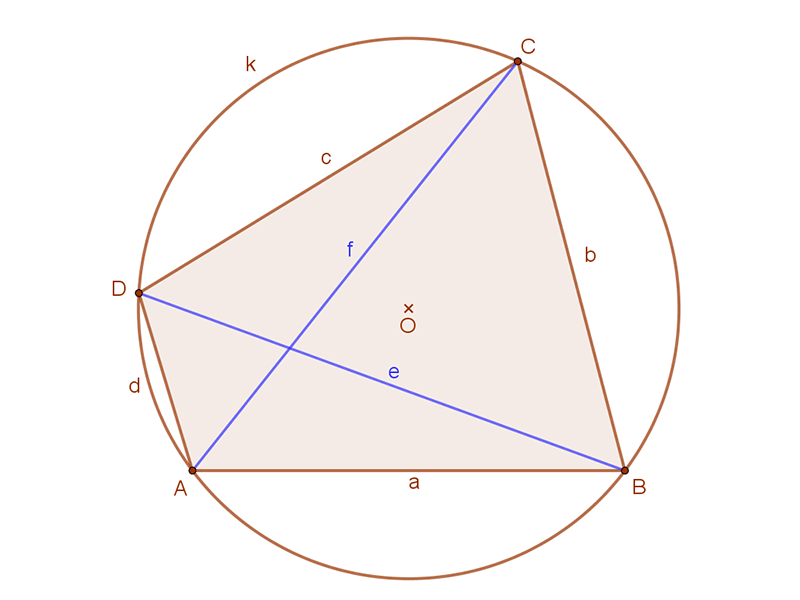
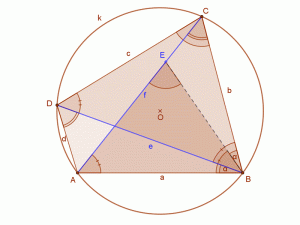
| A körbe írt négyszög átlóinak szorzata egyenlő a szemközti oldalak szorzatának összegével.
A mellékelt ábra jelöléseivel: AB⋅DC+BC⋅AD=AC⋅BD, azaz a⋅c+b⋅d=f⋅e. |
 |
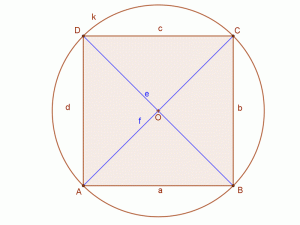
A tétel igazát könnyű belátni a nevezetes húrnégyszögek esetén. Például a négyzetre vagy a téglalapra.
 |
 |
| AB=BC=CD=DA=a. AC=f=BD=e=a∙√2. Így AB∙DC+BC∙AD=AC∙BD, hiszen a∙a+a∙a=a∙\( \sqrt{2} \)∙ a∙\( \sqrt{2} \). a2+a2=a2∙2. |
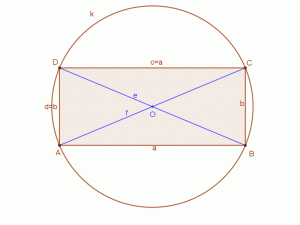
AB=CD=a; BC=DA=b. AC=BD=\( \sqrt{a^{2}+b^{2}} \) Így AB⋅DC+BC⋅AD=AC⋅BD, hiszen a∙a+b∙b=\( \sqrt{a^{2}+b^{2}} \) ∙\( \sqrt{a^{2}+b^{2}} \) a2+b2=a2+b2 |
Persze, egy általános húrnégyszög esetén már nem ennyire nyilvánvaló ez az összefüggés.
Bizonyítás:
A bizonyításhoz fel fogjuk használni a kerületi szögek tételét és a hasonló háromszögekre vonatkozó összefüggéseket.
| 1. Tekintsük a B csúcsnál lévő ABC szöget. A DB átló ezt a szöget két részre osztja. Legyen ∝ szög ennek a szögnek a nem nagyobbik része. A mellékelt ábrán ez az ABD∠ szög. | 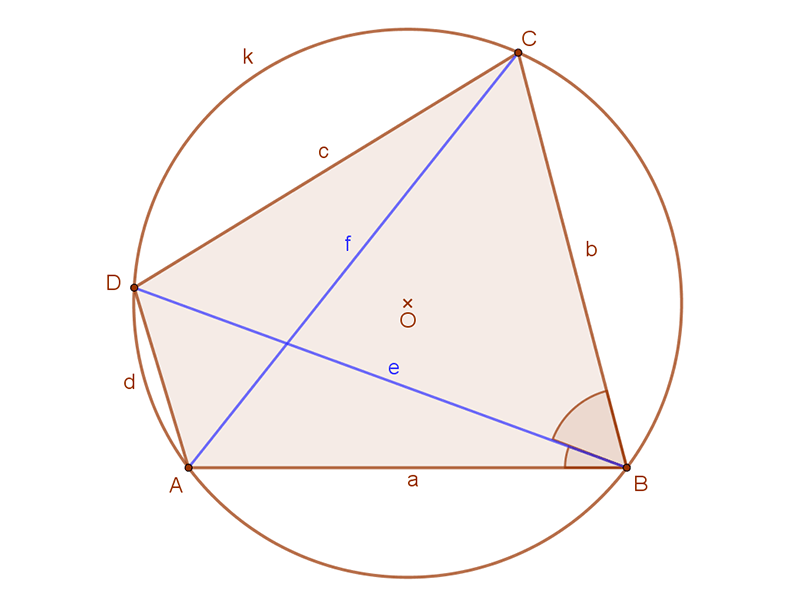 |
| 2. Mérjük rá az ABD∠=∝ szöget a BC oldalhoz a négyszög belseje felé. Az így kapott ABD∠ és CBE∠ szögek (∝) tehát egyenlők. | 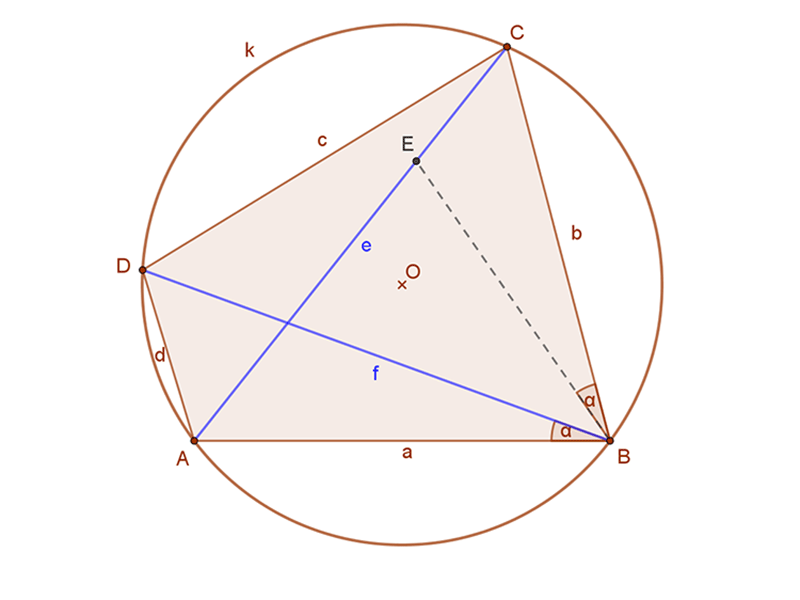 |
| 3. A D csúcsnál lévő ADB∠ megegyezik a C csúcsnál lévő ACB∠ szöggel. Hiszen mindkét szög az AB ívhez (húrhoz) tartozó kerületi szögek. Az ABD és EBC háromszögek hasonlók, hiszen két szögük megegyezik, ezért, az oldalaik aránya megegyezik. Tehát AD:BD=EC:BC. Ebből: EC=b∙d/e. |
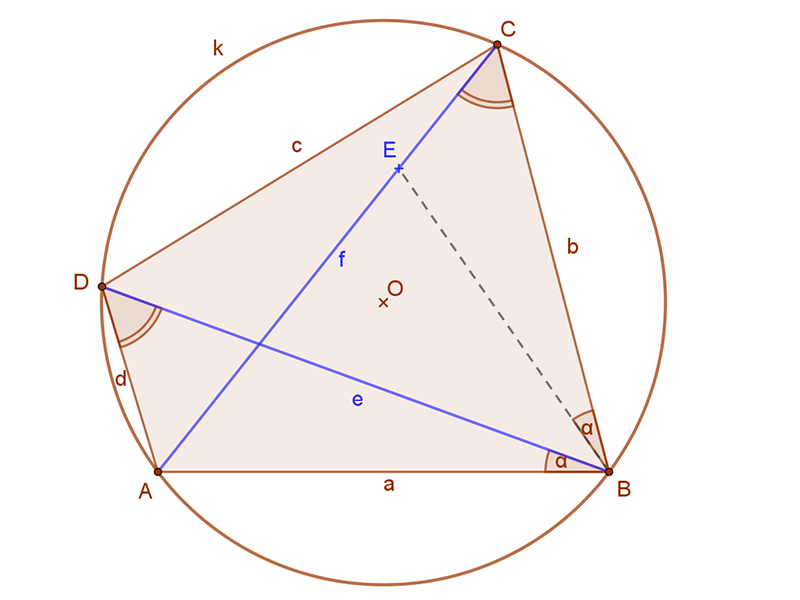 |
| 4. Ugyanakkor a BAC és a BDC (egy íves kétszer áthúzott) szögek is egyenlők, mert mindketten a BC ívhez tartozó kerületi szögek. |  |
| 5. Ugyancsak egyenlők az ABE és DBC (egy íves egyszer áthúzott) szögek is, hiszen mindketten tartalmazzák az egy íves (∝) szögeket és a DBE szöget. |  |
| 6. Az ABE és a DBC háromszögek tehát hasonlók, mivel az EAB és a CDB (egyíves, kétszer áthúzott) szögek, valamint az ABE és a DBC (egyíves, egyszer áthúzott) szögek egyenlők. Így az AEB és a DCB (egyíves) szögek is egyenlők. Az ABE és DBC háromszögek hasonlóságából megfelelő oldalak arányának egyenlősége következik. |
 |
Tehát: AE:AB=DC:BD
AE:a=c:e.
Ebből: AE=a∙c/e.
Adjuk most össze a 3. lépésben kapott EC=b∙d/e és a most kapott AE=a∙c/e kifejezéseket.
AE+EC=AC=a∙c/e+ b∙d/e.
AC=f=(a∙c+b∙d)/e
Ebből: e∙f=a∙c+b∙d.
Ezt kellett bizonyítani.
Lásd: dr. Gerőcs László: Azok a csodálatos húrnégyszögek


Comments are closed, but trackbacks and pingbacks are open.