Húrnégyszögek tétele

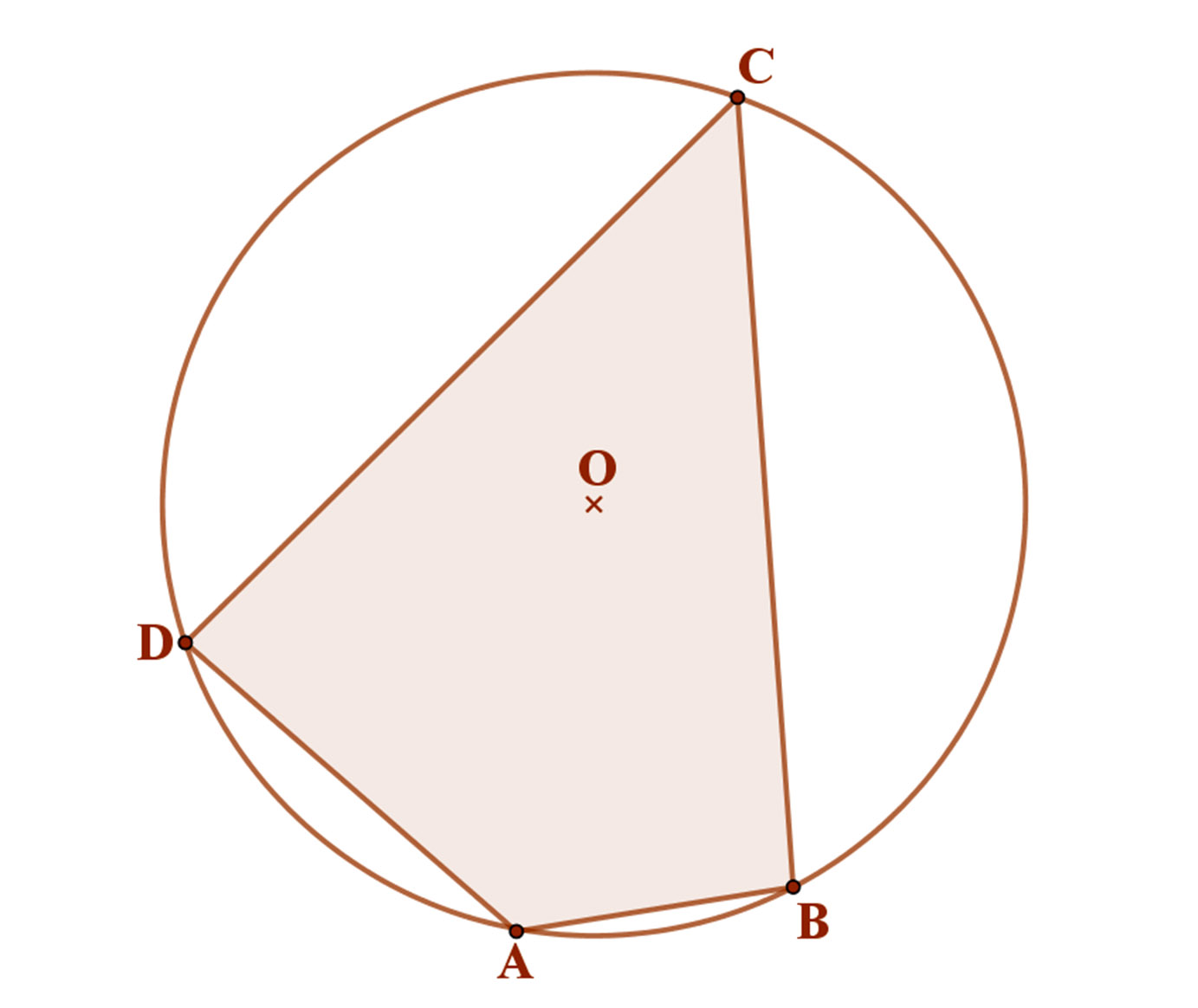
Definíció:

Azokat a konvex négyszögeket. amelynek oldalai egy körnek húrjai, húrnégyszögeknek nevezzük.

A húrnégyszögek oldalfelező merőlegesei egy pontban, a köré írt kör középpontjában metszik egymást.

Tétel:

Egy négyszög akkor és csak akkor húrnégyszög, ha szemközti szögeinek összege egyenlő.

A tétel két állítást tartalmaz:

1. Ha egy négyszög húrnégyszög, akkor szemközti szögeinek összege 180°.
2. Ha egy négyszög szemközti szögeinek összege 180°, akkor az a négyszög húrnégyszög.

1. Most az első állítást bizonyítjuk.

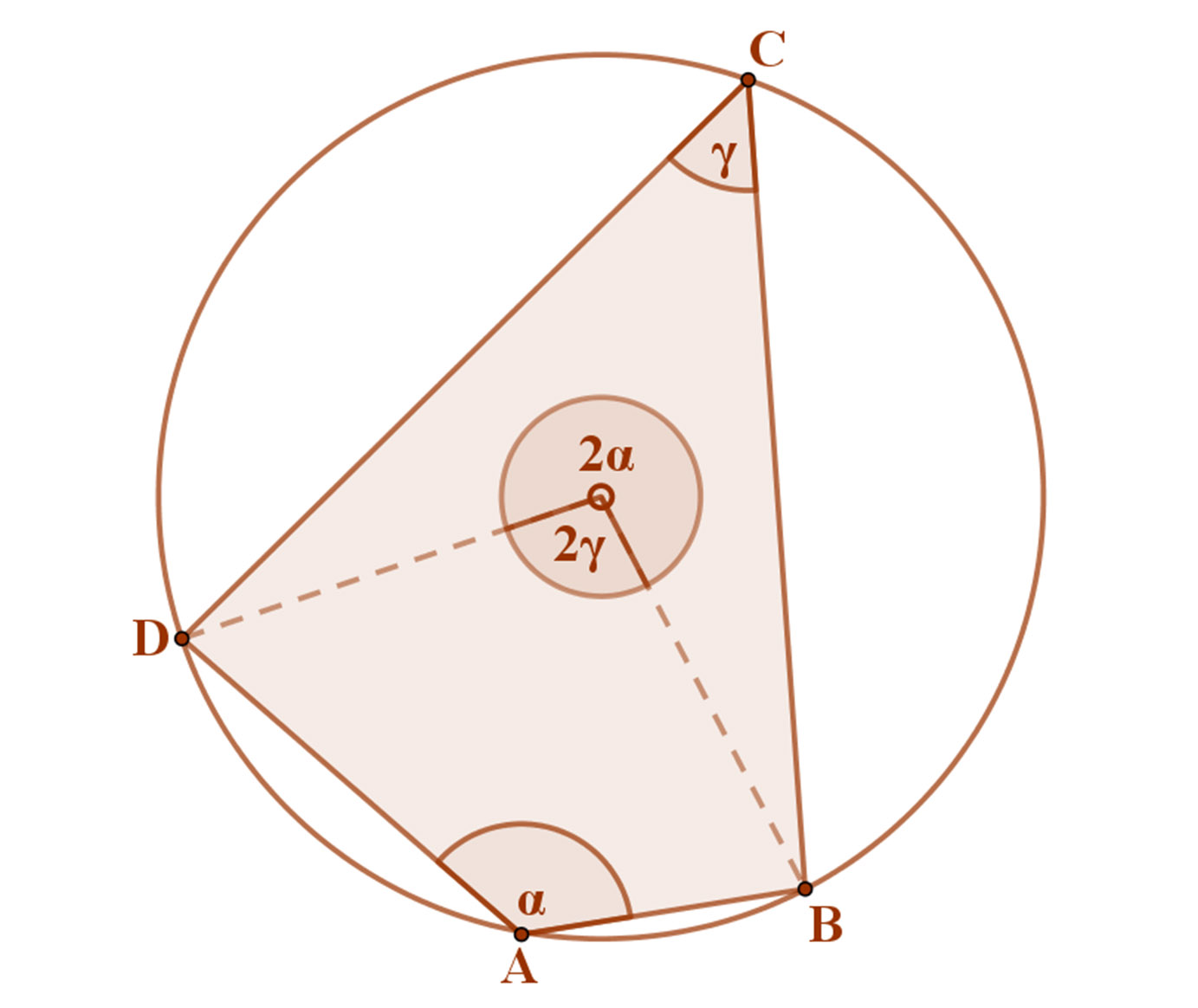
Ha egy négyszög húrnégyszög, akkor szemközti szögeinek összege 180°.

Kössük össze a húrnégyszög két szemközti csúcsát a kör középpontjával. A jobboldali ábrán a B és D csúcsokat.

A kerületi és középponti szögek tétele értelmében a BAD kerületi szöghöz (α) tartozó BOD középponti szög ennek kétszerese (2α). Ugyanígy, a BCD kerületi szöghöz (γ) tartozó BOD középponti szög ennek kétszerese (2γ).

Mivel 2α +2γ =360°, ezért α+γ =180°

Ezt kellett bizonyítani.

2. Ezután most a második állítást bizonyítjuk.

Azt fogjuk bizonyítani, hogyha egy négyszög szemközti szögeinek összege 180°, akkor az a négyszög húrnégyszög, tehát van csúcsain átmenő kör. 

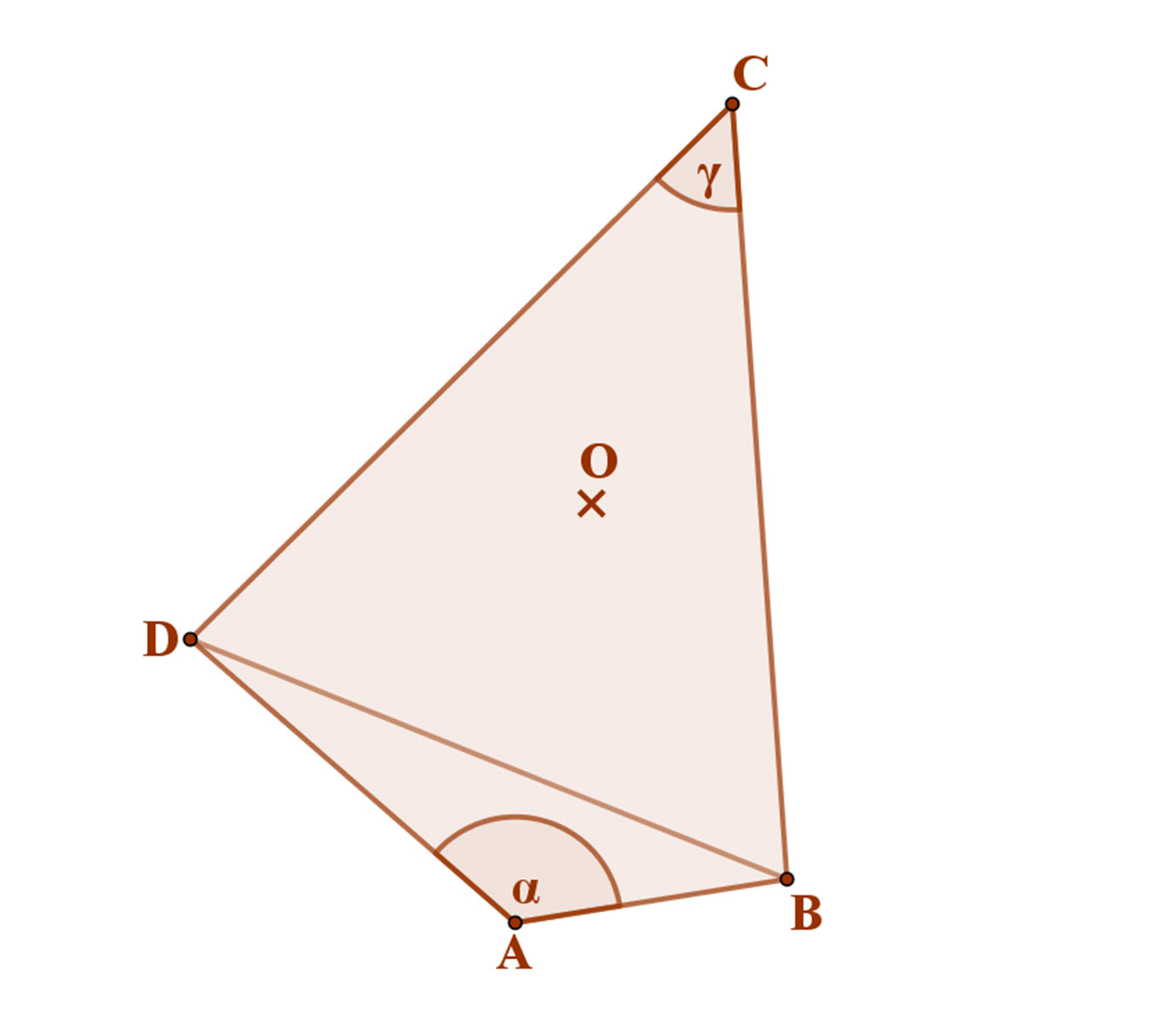Tekintsük az ABCD négyszöget, amelynek szemközti szögeinek összege 180°. Vegyük a mellékelt ábrát, α+γ=180°

Kössük össze az B és D csúcsokat, az α és a γ szögekkel szemközti átlót.

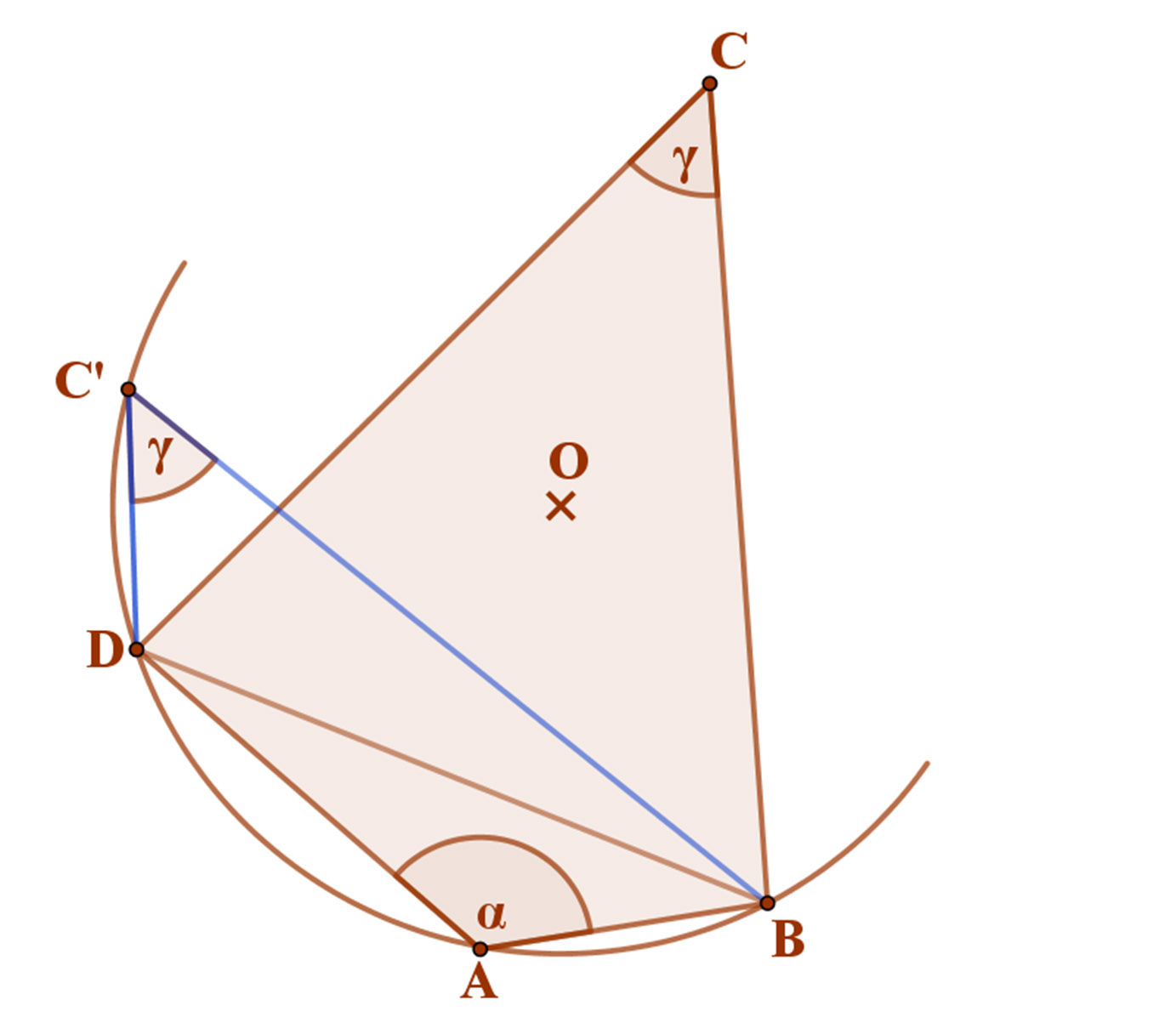Húzzuk meg az ABD háromszög köréírt körét. Ilyen mindig van. Azt még nem bizonyítottuk, hogy ez átmegy-e a negyedik C csúcson.

Jelöljük ki ennek a körívnek tetszőleges C’ pontját a B és D pontok között. (A BD átló azon oldalán, ahol a C pont van) Az ABC’D négyszög húrnégyszög, ezért a C’ csúcsnál lévő szög az α szög kiegészítő szöge, tehát a BC’D szög=γ.

Mivel az összes olyan pont, amelyből a BD átló γ szög alatt látszik, a BD átlóhoz tartozó szimmetrikus látóköríveken van, ezért a C pontnak szintén ugyanezen körívek valamelyikén kell lenni. Csak az a körív jöhet szóba, amelyik a BD átlónak az A csúccsal ellentétes oldalán van. A másik látóköríven nem lehet, mert akkor az ABCD négyszög nem konvex, hanem konkáv lenne.

Húrnégyszögekkel kapcsolatos a Ptolemaiosz tétel, amely szerint a húrnégyszög átlóinak szorzata egyenlő a szemközti oldalak szorzatának összegével.

Ehhez a témához ajánlható dr. Gerőcs László „Azok a csodálatos húrnégyszögek” című könyve.

Feladat: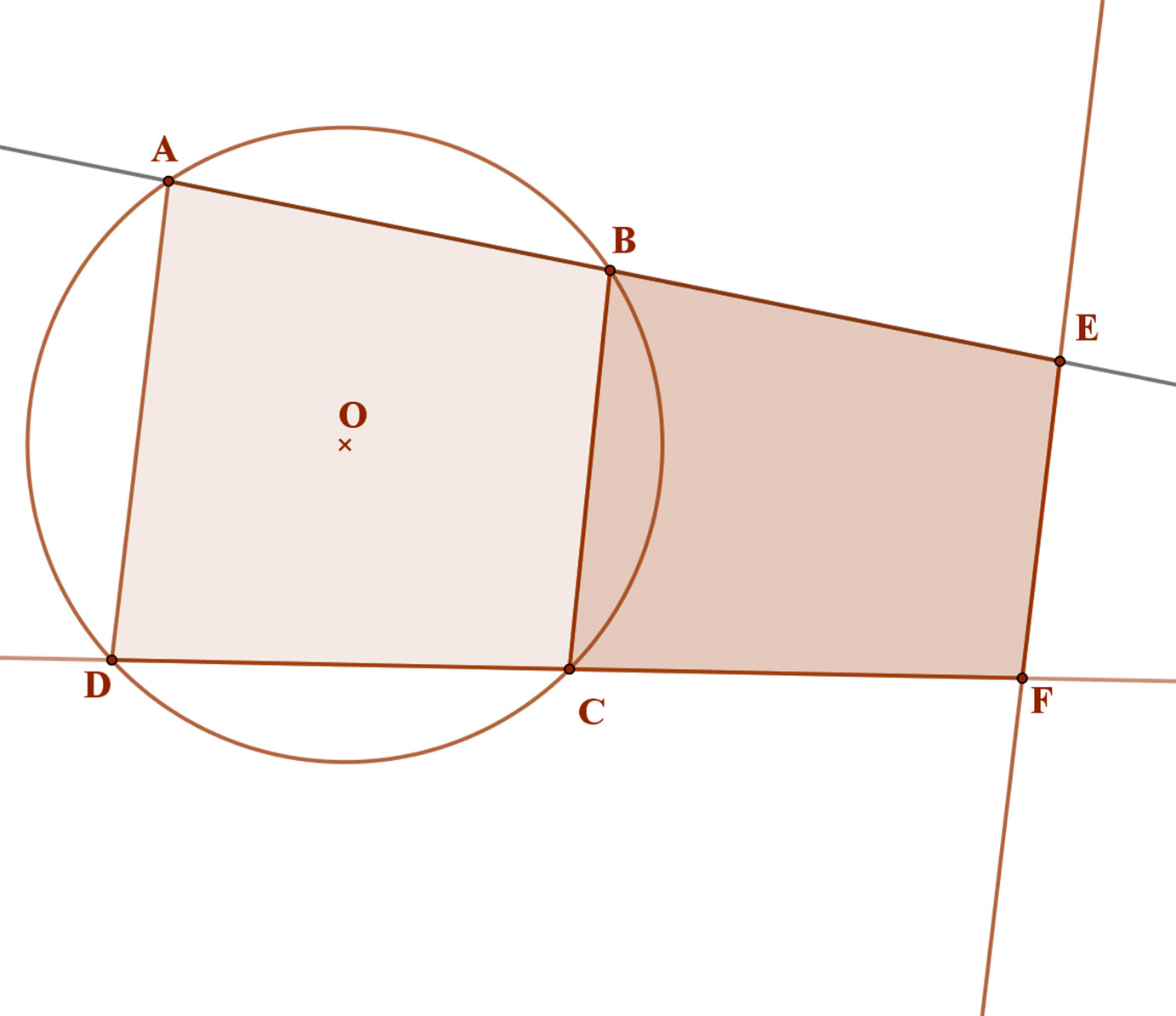

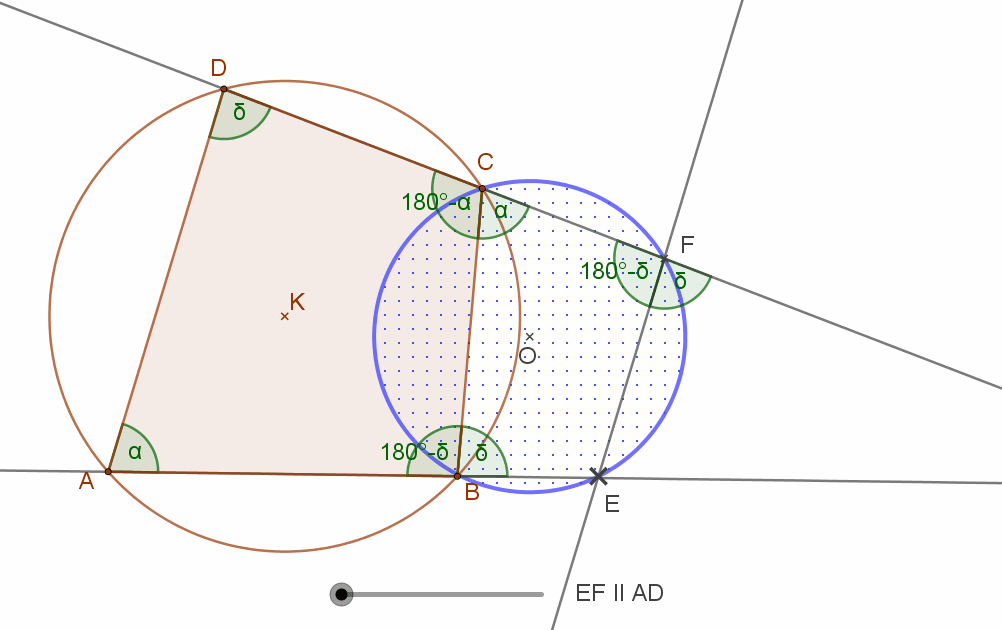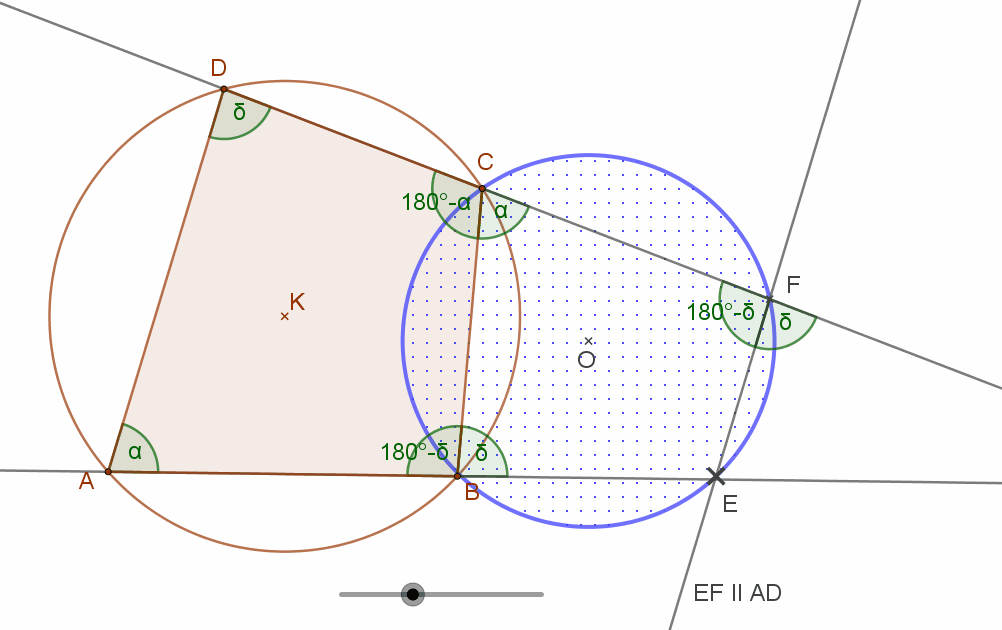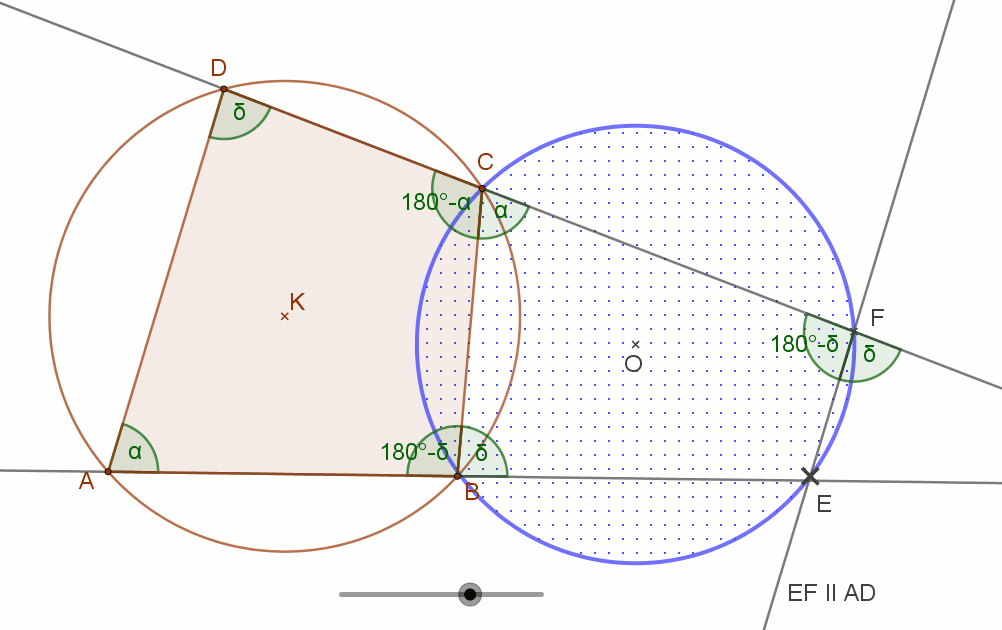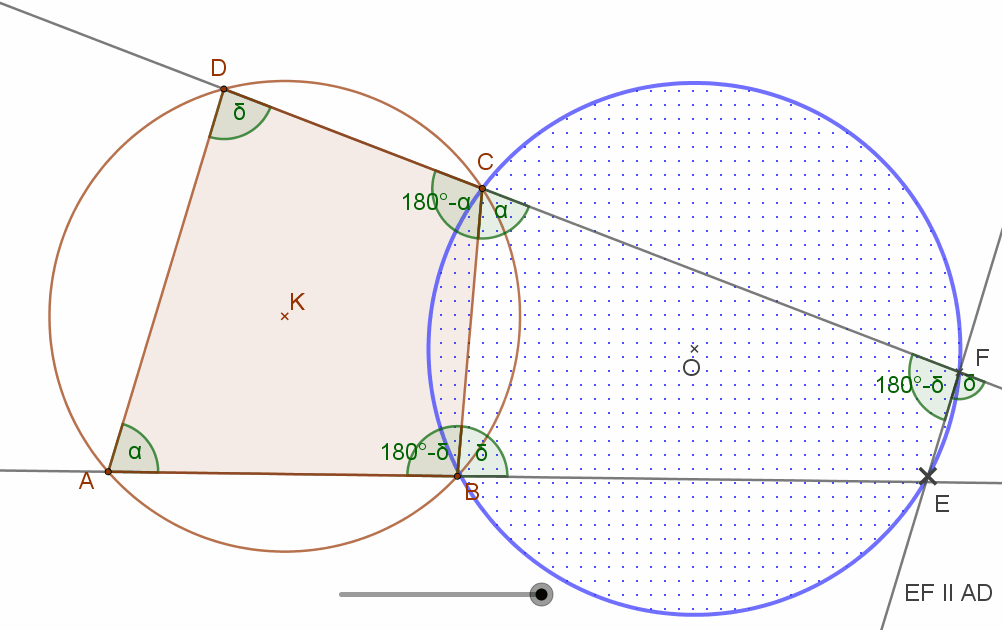
Egy kör négy pontja rendre A, B, C, D. A kör AB és CD szelőit a körön kívül messük AD-vel párhuzamos egyenessel. A mellékelt ábra szerint, a metszéspontok legyenek E és F! Mutassa meg, hogy EFCB húrnégyszög! 

(Összefoglaló feladatgyűjtemény 1772. feladat.)

Megoldás:

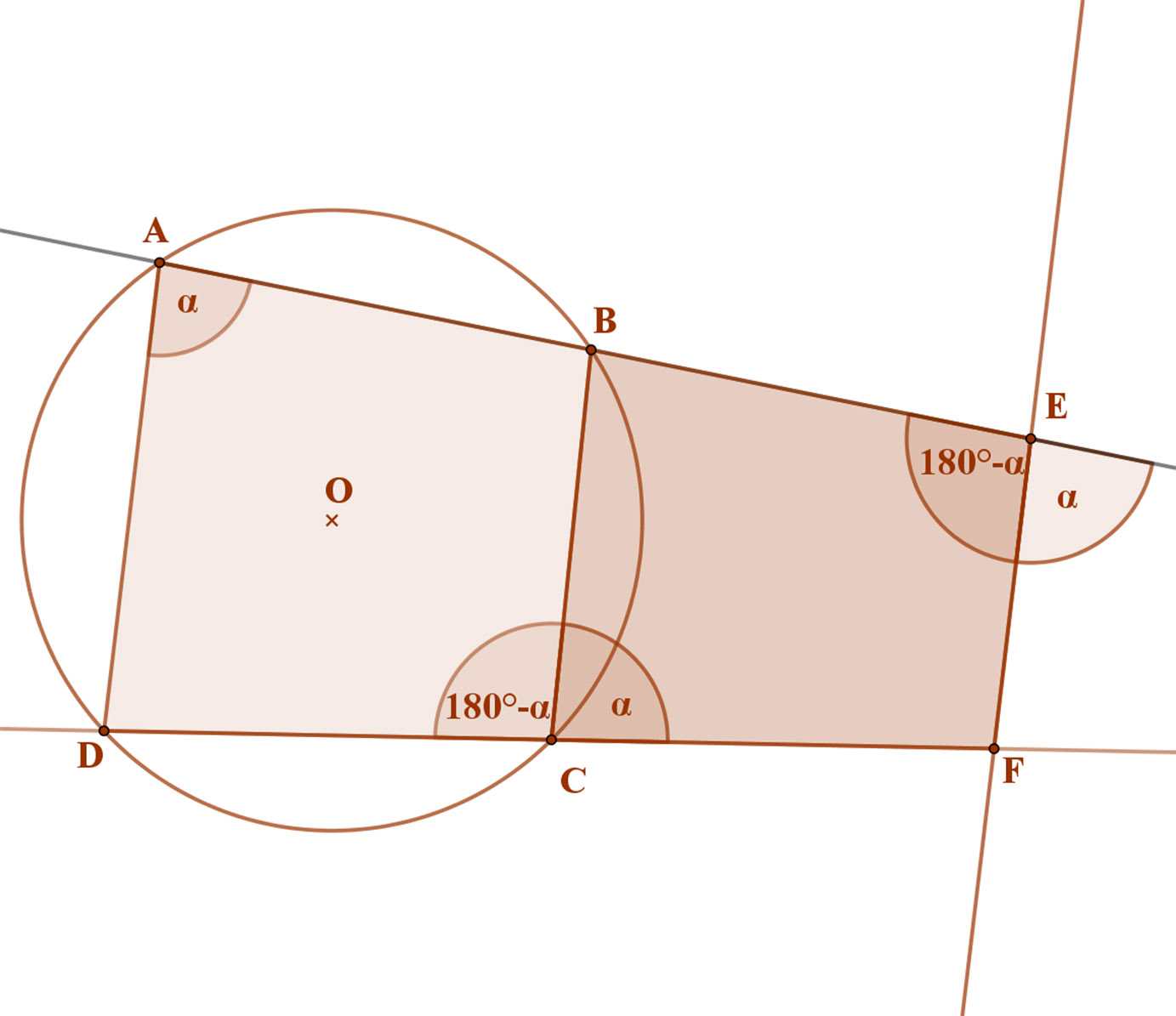Nevezzük az A csúcsnál lévő szöget α-nak. Mivel ABCD húrnégyszög, ezért az A csúccsal szemben, a C csúcsnál lévő szög a húrnégyszögek tétele érdekében 180°-α. Így a melletti FCB szög szintén α.

Mivel az EF egyenes párhuzamos az ABCD húrnégyszög AD húrjával, ezért az E csúcsnál lévő szög egyállású a DAB szöggel, így ez is α szög.

Emiatt a mellette lévő CBA szög 180°-α. Ez pedig azt jelenti, hogy a BEFC négyszögben a FCB=α. szöggel szembeni FEB szög 180°-α. Tehát a EFCB négyszög húrnégyszög.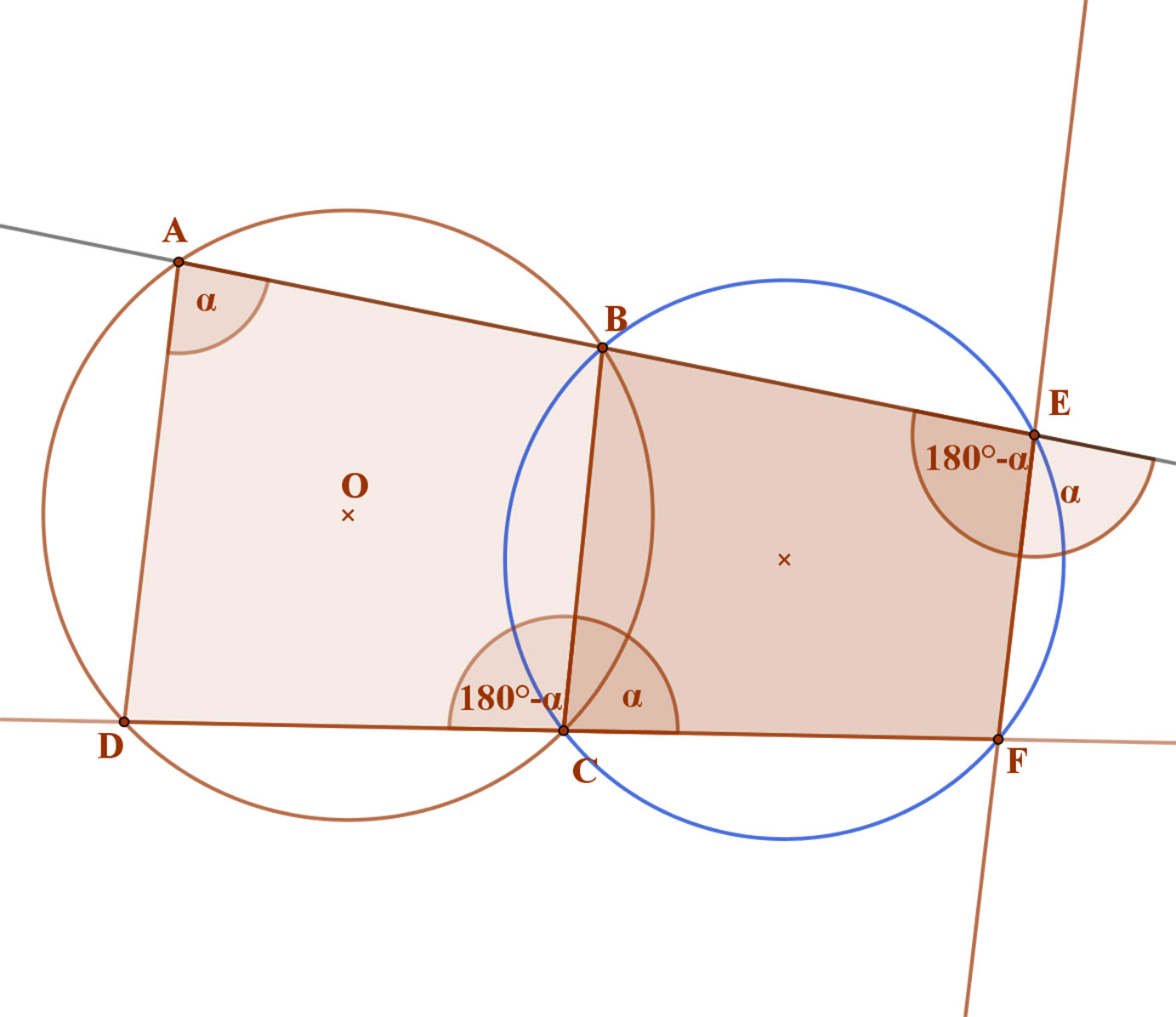

Mivel tehát EFCB négyszög húrnégyszög, kör rajzolható köréje, bárhol is legyen az AD-vel párhuzamos EF egyenes.